I’ve now finished my first grad course, Modelling of Multiphysics Systems, taught by Prof Piero Triverio.
I’ve posted notes for lectures and other material as I was taking the course, but now have an aggregated set of notes for the whole course posted.
This is now updated with all my notes from the lectures, solved problems, additional notes on auxillary topics I wanted to explore (like SVD), plus the notes from the Harmonic Balance report that Mike and I will be presenting in January.
This version of my notes also includes all the matlab figures regenerating using http://www.mathworks.
All in all, I’m pretty pleased with my notes for this course. They are a lot more readable than any of the ones I’ve done for the physics undergrad courses I was taking (https://peeterjoot.com/
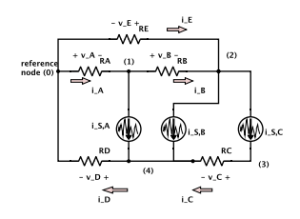
This was a fun course. I recall, back in ancient times when I was a first year student, being unsatisfied with all the ad-hoc strategies we used to solve circuits problems. This finally answers the questions of how to tackle things more systematically.
Here’s the contents outline for these notes:
Preface
Lecture notes
1 nodal analysis
1.1 In slides
1.2 Mechanical structures example
1.3 Assembling system equations automatically. Node/branch method
1.4 Nodal Analysis
1.5 Modified nodal analysis (MNA)
2 solving large systems
2.1 Gaussian elimination
2.2 LU decomposition
2.3 Problems
3 numerical errors and conditioning
3.1 Strict diagonal dominance
3.2 Exploring uniqueness and existence
3.3 Perturbation and norms
3.4 Matrix norm
4 singular value decomposition, and conditioning number
4.1 Singular value decomposition
4.2 Conditioning number
5 sparse factorization
5.1 Fill ins
5.2 Markowitz product
5.3 Markowitz reordering
5.4 Graph representation
6 gradient methods
6.1 Summary of factorization costs
6.2 Iterative methods
6.3 Gradient method
6.4 Recap: Summary of Gradient method
6.5 Conjugate gradient method
6.6 Full Algorithm
6.7 Order analysis
6.8 Conjugate gradient convergence
6.9 Gershgorin circle theorem
6.10 Preconditioning
6.11 Symmetric preconditioning
6.12 Preconditioned conjugate gradient
6.13 Problems
7 solution of nonlinear systems
7.1 Nonlinear systems
7.2 Richardson and Linear Convergence
7.3 Newton’s method
7.4 Solution of N nonlinear equations in N unknowns
7.5 Multivariable Newton’s iteration
7.6 Automatic assembly of equations for nonlinear system
7.7 Damped Newton’s method
7.8 Continuation parameters
7.9 Singular Jacobians
7.10 Struts and Joints, Node branch formulation
7.11 Problems
8 time dependent systems
8.1 Assembling equations automatically for dynamical systems
8.2 Numerical solution of differential equations
8.3 Forward Euler method
8.4 Backward Euler method
8.5 Trapezoidal rule (TR)
8.6 Nonlinear differential equations
8.7 Analysis, accuracy and stability (Dt ! 0)
8.8 Residual for LMS methods
8.9 Global error estimate
8.10 Stability
8.11 Stability (continued)
8.12 Problems
9 model order reduction
9.1 Model order reduction
9.2 Moment matching
9.3 Model order reduction (cont).
9.4 Moment matching
9.5 Truncated Balanced Realization (1000 ft overview)
9.6 Problems
Final report
10 harmonic balance
10.1 Abstract
10.2 Introduction
10.2.1 Modifications to the netlist syntax
10.3 Background
10.3.1 Discrete Fourier Transform
10.3.2 Harmonic Balance equations
10.3.3 Frequency domain representation of MNA equations
10.3.4 Example. RC circuit with a diode.
10.3.5 Jacobian
10.3.6 Newton’s method solution
10.3.7 Alternative handling of the non-linear currents and Jacobians
10.4 Results
10.4.1 Low pass filter
10.4.2 Half wave rectifier
10.4.3 AC to DC conversion
10.4.4 Bridge rectifier
10.4.5 Cpu time and error vs N
10.4.6 Taylor series non-linearities
10.4.7 Stiff systems
10.5 Conclusion
10.6 Appendices
10.6.1 Discrete Fourier Transform inversion
Appendices
a singular value decomposition
b basic theorems and definitions
c norton equivalents
d stability of discretized linear differential equations
e laplace transform refresher
f discrete fourier transform
g harmonic balance, rough notes
g.1 Block matrix form, with physical parameter ordering
g.2 Block matrix form, with frequency ordering
g.3 Representing the linear sources
g.4 Representing non-linear sources
g.5 Newton’s method
g.6 A matrix formulation of Harmonic Balance non-linear currents
h matlab notebooks
i mathematica notebooks
Index
Bibliography