[Click here for a PDF of this post with nicer formatting]
Motivation
Lance told me they’ve been covering the circumference of a circle in school this week. This made me think of the generalization of a circle, the ellipse, but I couldn’t recall what the circumference of an ellipse was. Sofia guessed \( \pi ( a + b ) \). Her reasoning was that this goes to \( 2 \pi r \) when the ellipse is circular, just like the area of an ellipse \( \pi a b \), goes to \( \pi a^2 \) in the circular limit. That seemed reasonable to me, but also strange since I didn’t recall any \( \pi ( a + b ) \) formula.
It turns out that there’s no closed form expression for the circumference of an ellipse, unless you count infinite series or special functions. Here I’ll calculate one expression for this circumference.
Geometry recap
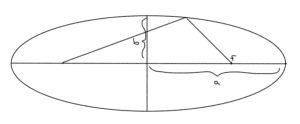
There’s two ways that I think of ellipses. One is the shape that you get when you put a couple tacks in a paper, and use a string and pencil to trace it out, as sketched in fig. 1.
The other is the basic vector parameterization of that same path
\begin{equation}\label{eqn:elipticCircumference:20}
\Br = ( a \cos\theta, b \sin\theta ).
\end{equation}
It’s been a long time since grade 11 when I would have taken it for granted that these two representations are identical. To do so, we’d have to know where the foci of the ellipse sit. Cheating a bit I find in [1] that the foci are located at
\begin{equation}\label{eqn:elipticCircumference:40}
\Bf_{\pm} = \pm \sqrt{ a^2 – b^2 } (1, 0).
\end{equation}
This and the equivalence of the pencil and tack representation of the ellipse can be verified by checking that the “length of the string” equals \( 2 a \) as expected.
That string length is
\begin{equation}\label{eqn:elipticCircumference:60}
\begin{aligned}
\Abs{ \Br – \Bf_{+} } + \Abs{ \Br – \Bf_{-} }
&=
\sqrt{ (a \cos\theta – f)^2 + b^2 \sin^2\theta }
+
\sqrt{ (a \cos\theta + f)^2 + b^2 \sin^2\theta } \\
&=
\sqrt{ a^2 \cos^2 \theta + f^2 – 2 a f \cos\theta + b^2 \lr{ 1 – \cos^2\theta } } \\
&\quad +
\sqrt{ a^2 \cos^2 \theta + f^2 + 2 a f \cos\theta + b^2 \lr{ 1 – \cos^2\theta } }.
\end{aligned}
\end{equation}
These square roots simplify nicely
\begin{equation}\label{eqn:elipticCircumference:80}
\begin{aligned}
\sqrt{ a^2 \cos^2 \theta + f^2 \pm 2 a f \cos\theta + b^2 \lr{ 1 – \cos^2\theta } }
&=
\sqrt{ (a^2 – b^2) \cos^2 \theta + a^2 – b^2 \pm 2 a f \cos\theta + b^2 } \\
&=
\sqrt{ f^2 \cos^2 \theta + a^2 \pm 2 a f \cos\theta } \\
&=
\sqrt{ (a \pm f \cos\theta)^2 } \\
&=
a \pm f \cos\theta.
\end{aligned}
\end{equation}
So the total length from one focus to a point on the ellipse, back to the other focus, is
\begin{equation}\label{eqn:elipticCircumference:100}
\Abs{ \Br – \Bf_{+} } + \Abs{ \Br – \Bf_{-} }
=
a + f \cos\theta + a – f \cos\theta = 2 a,
\end{equation}
as expected. That verifies that the trigonometric parameterization matches with the pencil and tacks representation of an ellipse (provided the foci are placed at the points \ref{eqn:elipticCircumference:40}).
Calculating the circumference
The circumference expression can almost be written by inspection. An element of the tangent vector along the curve is
\begin{equation}\label{eqn:elipticCircumference:340}
\frac{d\Br}{d\theta} = ( -a \sin\theta, b \cos\theta ),
\end{equation}
so the circumference is just a one liner
\begin{equation}\label{eqn:elipticCircumference:280}
C = 4 \int_0^{\pi/2} \sqrt{ a^2 \sin^2\theta + b^2 \cos^2 \theta} d\theta.
\end{equation}
The problem is that this one liner isn’t easy to evaluate. The square root can be put in a slightly simpler form in terms of the eccentricity, which is defined by
\begin{equation}\label{eqn:elipticCircumference:300}
e = \frac{f}{a} = \frac{\sqrt{a^2 – b^2}}{a} = \sqrt{ 1 – \frac{b^2}{a^2} }.
\end{equation}
Factoring out \( a \) and writing the sine as a cosine gives
\begin{equation}\label{eqn:elipticCircumference:320}
\begin{aligned}
C
&=
4 a \int_0^{\pi/2} \sqrt{ 1 – \cos^2\theta + \frac{b^2}{a^2} \cos^2 \theta} d\theta \\
&=
4 a \int_0^{\pi/2} \sqrt{ 1 + \lr{ \frac{b^2}{a^2} -1} \cos^2 \theta} d\theta \\
&=
4 a \int_0^{\pi/2} \sqrt{ 1 – e^2 \cos^2 \theta} d\theta.
\end{aligned}
\end{equation}
For the square root, it’s not hard to show that the fractional binomial expansion is
\begin{equation}\label{eqn:elipticCircumference:360}
\sqrt{1 + a}
=
1 – \sum_{k=1}^\infty \frac{(-a)^k}{2k – 1}\frac{ (2k – 1)!!}{(2k)!!},
\end{equation}
so the circumference is
\begin{equation}\label{eqn:elipticCircumference:380}
C
=
4 a \int_0^{\pi/2} d\theta
\lr{ 1 – \sum_{k=1}^\infty \frac{(e \cos\theta)^{2k}}{2k – 1}\frac{ (2k – 1)!!}{(2k)!!}}.
\end{equation}
Using \ref{eqn:elipticCircumference:260}, this is
\begin{equation}\label{eqn:elipticCircumference:400}
C
=
2 \pi a
–
4 a
\sum_{k=1}^\infty \frac{e^{2k}}{2k – 1}\frac{ (2k – 1)!!}{(2k)!!}
\frac{(2k – 1)!!}{(2k)!!} \frac{\pi}{2}
\end{equation}
\begin{equation}\label{eqn:elipticCircumference:420}
\boxed{
C
=
2 \pi a \lr{ 1 –
\sum_{k=1}^\infty \frac{e^{2k}}{2k – 1} \lr{ \frac{ (2k – 1)!!}{(2k)!!} }^2
}.
}
\end{equation}
Observe that this does reduce to \( 2 \pi r \) for the circle (where \( e = 0 \)), and certainly isn’t as nice as \( \pi (a + b) \).
Appendix. Integral of even cosine powers.
The integral
\begin{equation}\label{eqn:elipticCircumference:120}
\int_0^{\pi/2} \cos^{2k} \theta d\theta
\end{equation}
can be evaluated using integration by parts.
\begin{equation}\label{eqn:elipticCircumference:140}
\begin{aligned}
\int_0^{\pi/2} \cos^{2k} \theta d\theta
&=
\int_0^{\pi/2} \cos^{2k-1} \theta \frac{d \sin\theta}{d\theta} d\theta \\
&=
\evalrange{
\cos^{2k-1} \theta \sin\theta
}{0}{\pi/2}
–
(2 k -1)
\int_0^{\pi/2} \cos^{2k-2} \theta (-\sin\theta) \sin\theta d\theta \\
&=
(2 k -1)
\int_0^{\pi/2} \cos^{2k-2} \theta (1 – \cos^2\theta) d\theta \\
&=
(2 k -1)
\int_0^{\pi/2} \cos^{2k-2} \theta d\theta
–
(2 k -1)
\int_0^{\pi/2} \cos^{2k} \theta d\theta.
\end{aligned}
\end{equation}
Bringing the \( 2k \) power integral to the other side and solving for the original integral gives a recurrence relation
\begin{equation}\label{eqn:elipticCircumference:160}
\begin{aligned}
\int_0^{\pi/2} \cos^{2k} \theta d\theta
&= \frac{2 k – 1}{2 k}
\int_0^{\pi/2} \cos^{2k -2} \theta d\theta \\
&=
\frac{2 k – 1}{2 k}
\frac{2 k – 3}{2 k – 2}
\int_0^{\pi/2} \cos^{2k -4} \theta d\theta \\
&=
\frac{2 k – 1}{2 k}
\frac{2 k – 3}{2 k – 2}
\cdots
\frac{3}{4}
\int_0^{\pi/2} \cos^{2} \theta d\theta.
\end{aligned}
\end{equation}
This last can also be solved using integration by parts
\begin{equation}\label{eqn:elipticCircumference:180}
\begin{aligned}
\int_0^{\pi/2} \cos^{2} \theta d\theta
&=
\int_0^{\pi/2} \cos \theta \frac{d \sin\theta}{d\theta} d\theta \\
&=
–
\int_0^{\pi/2} (-\sin \theta) \sin\theta d\theta \\
&=
\int_0^{\pi/2} \lr{ 1 – \cos^2 \theta } d\theta,
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:elipticCircumference:200}
\begin{aligned}
\Abs{ \Br – \Bf_{+} } + \Abs{ \Br – \Bf_{-} }
&=
\int_0^{\pi/2} \cos^{2} \theta d\theta \\
&=
\inv{2} \frac{\pi}{2}.
\end{aligned}
\end{equation}
This gives
\begin{equation}\label{eqn:elipticCircumference:220}
\int_0^{\pi/2} \cos^{2k} \theta d\theta
=
\frac{2 k – 1}{2 k}
\frac{2 k – 3}{2 k – 2}
\cdots
\frac{3}{4}
\frac{1}{2}
\frac{\pi}{2}.
\end{equation}
Using the double factorial notation (factorial that skips every other value), this is
\begin{equation}\label{eqn:elipticCircumference:260}
\boxed{
\int_0^{\pi/2} \cos^{2k} \theta d\theta
=
\frac{(2k – 1)!!}{(2k)!!} \frac{\pi}{2}
}
\end{equation}
References
[1] Wikipedia. Ellipse — wikipedia, the free encyclopedia, 2015. URL https://en.wikipedia.org/w/index.php?title=Ellipse&oldid=650116160. [Online; accessed 9-March-2015].