[Click here for a PDF of this post with nicer formatting]
The integral forms of Maxwell’s equations can be used to derive relations for the tangential and normal field components to the sources. These relations were mentioned in class. It’s a little late, but lets go over the derivation. This isn’t all review from first year electromagnetism since we are now using a magnetic source modifications of Maxwell’s equations.
The derivation below follows that of [1] closely, but I am trying it myself to ensure that I understand the assumptions.
The two infinitesimally thin pillboxes of fig. 1, and fig. 2 are used in the argument.
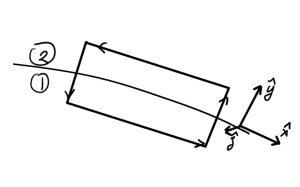
fig. 2: Pillboxes for tangential and normal field relations
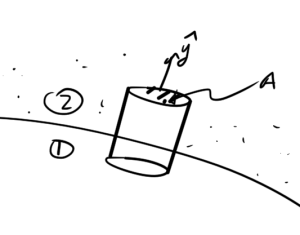
fig. 1: Pillboxes for tangential and normal field relations
Maxwell’s equations with both magnetic and electric sources are
\begin{equation}\label{eqn:normalAndTangentialFields:20}
\spacegrad \cross \boldsymbol{\mathcal{E}} = -\PD{t}{\boldsymbol{\mathcal{B}}} -\boldsymbol{\mathcal{M}}
\end{equation}
\begin{equation}\label{eqn:normalAndTangentialFields:40}
\spacegrad \cross \boldsymbol{\mathcal{H}} = \boldsymbol{\mathcal{J}} + \PD{t}{\boldsymbol{\mathcal{D}}}
\end{equation}
\begin{equation}\label{eqn:normalAndTangentialFields:60}
\spacegrad \cdot \boldsymbol{\mathcal{D}} = \rho_\textrm{e}
\end{equation}
\begin{equation}\label{eqn:normalAndTangentialFields:80}
\spacegrad \cdot \boldsymbol{\mathcal{B}} = \rho_\textrm{m}.
\end{equation}
After application of Stokes’ and the divergence theorems Maxwell’s equations have the integral form
\begin{equation}\label{eqn:normalAndTangentialFields:100}
\oint \boldsymbol{\mathcal{E}} \cdot d\Bl = -\int d\BA \cdot \lr{ \PD{t}{\boldsymbol{\mathcal{B}}} + \boldsymbol{\mathcal{M}} }
\end{equation}
\begin{equation}\label{eqn:normalAndTangentialFields:120}
\oint \boldsymbol{\mathcal{H}} \cdot d\Bl = \int d\BA \cdot \lr{ \PD{t}{\boldsymbol{\mathcal{D}}} + \boldsymbol{\mathcal{J}} }
\end{equation}
\begin{equation}\label{eqn:normalAndTangentialFields:140}
\int_{\partial V} \boldsymbol{\mathcal{D}} \cdot d\BA
=
\int_V \rho_\textrm{e}\,dV
\end{equation}
\begin{equation}\label{eqn:normalAndTangentialFields:160}
\int_{\partial V} \boldsymbol{\mathcal{B}} \cdot d\BA
=
\int_V \rho_\textrm{m}\,dV.
\end{equation}
Maxwell-Faraday equation
First consider one of the loop integrals, like \ref{eqn:normalAndTangentialFields:100}. For an infinestismal loop, that integral is
\begin{equation}\label{eqn:normalAndTangentialFields:180}
\begin{aligned}
\oint \boldsymbol{\mathcal{E}} \cdot d\Bl
&\approx
\mathcal{E}^{(1)}_x \Delta x
+ \mathcal{E}^{(1)} \frac{\Delta y}{2}
+ \mathcal{E}^{(2)} \frac{\Delta y}{2}
-\mathcal{E}^{(2)}_x \Delta x
– \mathcal{E}^{(2)} \frac{\Delta y}{2}
– \mathcal{E}^{(1)} \frac{\Delta y}{2} \\
&\approx
\lr{ \mathcal{E}^{(1)}_x
-\mathcal{E}^{(2)}_x } \Delta x
+ \inv{2} \PD{x}{\mathcal{E}^{(2)}} \Delta x \Delta y
+ \inv{2} \PD{x}{\mathcal{E}^{(1)}} \Delta x \Delta y.
\end{aligned}
\end{equation}
We let \( \Delta y \rightarrow 0 \) which kills off all but the first difference term.
The RHS of \ref{eqn:normalAndTangentialFields:180} is approximately
\begin{equation}\label{eqn:normalAndTangentialFields:200}
-\int d\BA \cdot \lr{ \PD{t}{\boldsymbol{\mathcal{B}}} + \boldsymbol{\mathcal{M}} }
\approx
– \Delta x \Delta y \lr{ \PD{t}{\mathcal{B}_z} + \mathcal{M}_z }.
\end{equation}
If the magnetic field contribution is assumed to be small in comparison to the magnetic current (i.e. infinite magnetic conductance), and if a linear magnetic current source of the form is also assumed
\begin{equation}\label{eqn:normalAndTangentialFields:220}
\boldsymbol{\mathcal{M}}_s = \lim_{\Delta y \rightarrow 0} \lr{\boldsymbol{\mathcal{M}} \cdot \zcap} \zcap \Delta y,
\end{equation}
then the Maxwell-Faraday equation takes the form
\begin{equation}\label{eqn:normalAndTangentialFields:240}
\lr{ \mathcal{E}^{(1)}_x
-\mathcal{E}^{(2)}_x } \Delta x
\approx
– \Delta x \boldsymbol{\mathcal{M}}_s \cdot \zcap.
\end{equation}
While \( \boldsymbol{\mathcal{M}} \) may have components that are not normal to the interface, the surface current need only have a normal component, since only that component contributes to the surface integral.
The coordinate expression of \ref{eqn:normalAndTangentialFields:240} can be written as
\begin{equation}\label{eqn:normalAndTangentialFields:260}
– \boldsymbol{\mathcal{M}}_s \cdot \zcap
=
\lr{ \boldsymbol{\mathcal{E}}^{(1)} -\boldsymbol{\mathcal{E}}^{(2)} } \cdot \lr{ \ycap \cross \zcap }
=
\lr{ \lr{ \boldsymbol{\mathcal{E}}^{(1)} -\boldsymbol{\mathcal{E}}^{(2)} } \cross \ycap } \cdot \zcap.
\end{equation}
This is satisfied when
\begin{equation}\label{eqn:normalAndTangentialFields:280}
\boxed{
\lr{ \boldsymbol{\mathcal{E}}^{(1)} -\boldsymbol{\mathcal{E}}^{(2)} } \cross \ncap = – \boldsymbol{\mathcal{M}}_s,
}
\end{equation}
where \( \ncap \) is the normal between the interfaces. I’d failed to understand when reading this derivation initially, how the \( \boldsymbol{\mathcal{B}} \) contribution was killed off. i.e. If the vanishing area in the surface integral kills off the \( \boldsymbol{\mathcal{B}} \) contribution, why do we have a \( \boldsymbol{\mathcal{M}} \) contribution left. The key to this is understanding that this magnetic current is considered to be confined very closely to the surface getting larger as \( \Delta y \) gets smaller.
Also note that the units of \( \boldsymbol{\mathcal{M}}_s \) are volts/meter like the electric field (not volts/squared-meter like \( \boldsymbol{\mathcal{M}} \).)
Ampere’s law
As above, assume a linear electric surface current density of the form
\begin{equation}\label{eqn:normalAndTangentialFields:300}
\boldsymbol{\mathcal{J}}_s = \lim_{\Delta y \rightarrow 0} \lr{\boldsymbol{\mathcal{J}} \cdot \ncap} \ncap \Delta y,
\end{equation}
in units of amperes/meter (not amperes/meter-squared like \( \boldsymbol{\mathcal{J}} \).)
To apply the arguments above to Ampere’s law, only the sign needs to be adjusted
\begin{equation}\label{eqn:normalAndTangentialFields:290}
\boxed{
\lr{ \boldsymbol{\mathcal{H}}^{(1)} -\boldsymbol{\mathcal{H}}^{(2)} } \cross \ncap = \boldsymbol{\mathcal{J}}_s.
}
\end{equation}
Gauss’s law
Using the cylindrical pillbox surface with radius \( \Delta r \), height \( \Delta y \), and top and bottom surface areas \( \Delta A = \pi \lr{\Delta r}^2 \), the LHS of Gauss’s law \ref{eqn:normalAndTangentialFields:140} expands to
\begin{equation}\label{eqn:normalAndTangentialFields:320}
\begin{aligned}
\int_{\partial V} \boldsymbol{\mathcal{D}} \cdot d\BA
&\approx
\mathcal{D}^{(2)}_y \Delta A
+ \mathcal{D}^{(2)}_\rho 2 \pi \Delta r \frac{\Delta y}{2}
+ \mathcal{D}^{(1)}_\rho 2 \pi \Delta r \frac{\Delta y}{2}
-\mathcal{D}^{(1)}_y \Delta A \\
&\approx
\lr{ \mathcal{D}^{(2)}_y
-\mathcal{D}^{(1)}_y } \Delta A.
\end{aligned}
\end{equation}
As with the Stokes integrals above it is assumed that the height is infinestimal with respect to the radial dimension. Letting that height \( \Delta y \rightarrow 0 \) kills off the radially directed contributions of the flux through the sidewalls.
The RHS expands to approximately
\begin{equation}\label{eqn:normalAndTangentialFields:340}
\int_V \rho_\textrm{e}\,dV
\approx
\Delta A \Delta y \rho_\textrm{e}.
\end{equation}
Define a highly localized surface current density (coulombs/meter-squared) as
\begin{equation}\label{eqn:normalAndTangentialFields:360}
\sigma_\textrm{e} = \lim_{\Delta y \rightarrow 0} \Delta y \rho_\textrm{e}.
\end{equation}
Equating \ref{eqn:normalAndTangentialFields:340} with \ref{eqn:normalAndTangentialFields:320} gives
\begin{equation}\label{eqn:normalAndTangentialFields:380}
\lr{ \mathcal{D}^{(2)}_y
-\mathcal{D}^{(1)}_y } \Delta A
=
\Delta A \sigma_\textrm{e},
\end{equation}
or
\begin{equation}\label{eqn:normalAndTangentialFields:400}
\boxed{
\lr{ \boldsymbol{\mathcal{D}}^{(2)} – \boldsymbol{\mathcal{D}}^{(1)} } \cdot \ncap = \sigma_\textrm{e}.
}
\end{equation}
Gauss’s law for magnetism
The same argument can be applied to the magnetic flux. Define a highly localized magnetic surface current density (webers/meter-squared) as
\begin{equation}\label{eqn:normalAndTangentialFields:440}
\sigma_\textrm{m} = \lim_{\Delta y \rightarrow 0} \Delta y \rho_\textrm{m},
\end{equation}
yielding the boundary relation
\begin{equation}\label{eqn:normalAndTangentialFields:420}
\boxed{
\lr{ \boldsymbol{\mathcal{B}}^{(2)} – \boldsymbol{\mathcal{B}}^{(1)} } \cdot \ncap = \sigma_\textrm{m}.
}
\end{equation}
References
[1] Constantine A Balanis. Advanced engineering electromagnetics, volume 20, chapter Time-varying and time-harmonic electromagnetic fields. Wiley New York, 1989.
Like this:
Like Loading...


