Day: September 26, 2015

Grade 11 physics handout: “The Big Five … in Physics”?

September 26, 2015 math and physics play ,

[Click here for a PDF of this post with nicer formatting]

Motivation

Check out fig. 1, a handout given to my daughter has a handout from her grade 11 physics class, titled “The Big Five”, covering some dynamics equations.

fig. 1. The Big Five... in Physics

fig. 1. The Big Five… in Physics

I found this handout disorienting. Part of that disorientation is because of the weird African animal theme which I couldn’t see the rationale for. Aurora showed me that the second equation can be outlined with an elephant, apparently justifying the animal theme. The equations themselves are not in a form that I would have expected, and have a lot of redundancy built in. The assumptions required for these equations to be valid are also not stated. Those equations are

\begin{equation}\label{eqn:theBigFivePhysics:40}
v_2 = v_1 + a \Delta t
\end{equation}
\begin{equation}\label{eqn:theBigFivePhysics:60}
\Delta d = \inv{2} \lr{ v_1 + v_2 } \Delta t
\end{equation}
\begin{equation}\label{eqn:theBigFivePhysics:80}
\Delta d = v_1 \Delta t + \inv{2} a \lr{\Delta t}^2
\end{equation}
\begin{equation}\label{eqn:theBigFivePhysics:100}
\Delta d = v_2 \Delta t – \inv{2} a \lr{\Delta t}^2
\end{equation}
\begin{equation}\label{eqn:theBigFivePhysics:120}
v_2^2 = v_1^2 + 2 a \Delta d.
\end{equation}

Reverse engineering “the big five”.

Difference of velocity

The first equation \ref{eqn:theBigFivePhysics:40} is just a discrete version of the definition of scalar acceleration

\begin{equation}\label{eqn:theBigFivePhysics:140}
a = \frac{dv}{dt}.
\end{equation}

The approximation of that is

\begin{equation}\label{eqn:theBigFivePhysics:160}
a = \frac{\Delta v}{\Delta t},
\end{equation}

or

\begin{equation}\label{eqn:theBigFivePhysics:180}
\Delta v = v_2 – v_1 = a \Delta t.
\end{equation}

Constant acceleration

Next in the list, it’s clear that the equation(s) for \( \Delta d \) is really based on an assumption of constant acceleration. In fact, all four of the next equations are nothing more than variations of

\begin{equation}\label{eqn:theBigFivePhysics:200}
v = a t.
\end{equation}

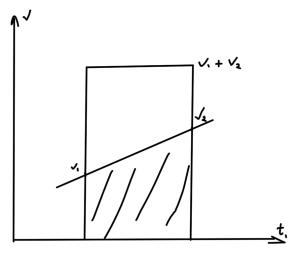
To arrive at fig. 2.

fig. 2. Displacement as area under the curve.

fig. 2. Displacement as area under the curve.

Should we wish to integrate, it’s the second simplest integral we could possibly do

\begin{equation}\label{eqn:theBigFivePhysics:220}
\begin{aligned}
\Delta x
&= \int_{t_1}^{t_2} v(t) dt \\
&= \int_{t_1}^{t_2} a t dt \\
&= \inv{2} a \lr{ t_2^2 – t_1^2 } \\
&= \inv{2} a \Delta t \lr{ t_2 + t_1 }.
\end{aligned}
\end{equation}

This looks a little different than what’s on the formula cheet, but since (for constant acceleration) we have

\begin{equation}\label{eqn:theBigFivePhysics:240}
t = \frac{v}{a},
\end{equation}

this can be written as

\begin{equation}\label{eqn:theBigFivePhysics:260}
\begin{aligned}
\Delta x
&= \inv{2} a \Delta t \lr{ \frac{v_2}{a} + \frac{v_1}{a} } \\
&= \inv{2} \Delta t \lr{ v_1 + v_2 },
\end{aligned}
\end{equation}

as found on the formula sheet (except for them using \( \Delta d \) for the difference in position .)

Each of the next equations follow from straight algebra

\begin{equation}\label{eqn:theBigFivePhysics:280}
\begin{aligned}
\Delta x – v_1 \Delta t
&= \inv{2} \Delta t \lr{ v_1 + v_2 } – v_1 \Delta t \\
&= \inv{2} \Delta t \lr{ -v_1 + v_2 } \\
&= \inv{2} \lr{\Delta t}^2 \frac{\Delta v}{\Delta t} \\
&= \inv{2} a \lr{\Delta t}^2,
\end{aligned}
\end{equation}

and

\begin{equation}\label{eqn:theBigFivePhysics:300}
\begin{aligned}
\Delta x – v_2 \Delta t
&= \inv{2} \Delta t \lr{ v_1 + v_2 } – v_2 \Delta t \\
&= \inv{2} \Delta t \lr{ v_1 – v_2 } \\
&= -\inv{2} \lr{\Delta t}^2 \frac{\Delta v}{\Delta t} \\
&= -\inv{2} a \lr{\Delta t}^2,
\end{aligned}
\end{equation}

and finally

\begin{equation}\label{eqn:theBigFivePhysics:320}
\begin{aligned}
\Delta x
&= \inv{2} a \lr{ t_2^2 – t_1^2 } \\
&= \inv{2 a } \lr{ v_2^2 – v_1^2 }.
\end{aligned}
\end{equation}

A better set of equations.

If I had to write these “big five” equation, I’d be more inclined to write them as

\begin{equation}\label{eqn:theBigFivePhysics:360}
a = \frac{\Delta v}{\Delta t}
\end{equation}
\begin{equation}\label{eqn:theBigFivePhysics:380}
v = a t = \frac{\Delta x}{\Delta t}
\end{equation}
\begin{equation}\label{eqn:theBigFivePhysics:400}
\Delta x = \int_{t_1}^{t_2} v dt = \inv{2} a \lr{ t_2^2 – t_1^2 }
\end{equation}
\begin{equation}\label{eqn:theBigFivePhysics:420}
t_1 = \frac{v_1}{a}
\end{equation}
\begin{equation}\label{eqn:theBigFivePhysics:440}
t_2 = \frac{v_2}{a}.
\end{equation}

Anything more than that is just algebra. The last two could be omitted since they really follow from \ref{eqn:theBigFivePhysics:380}. For high school where calculus isn’t known, I’d swap out \ref{eqn:theBigFivePhysics:400} for \ref{eqn:theBigFivePhysics:60} which can be derived graphically by understanding that the distance is the area under the velocity curve.

I’d also leave out all mentions of big African animals, which is, just plain weird!

Lagrangian for magnetic portion of Lorentz force

September 26, 2015 phy1520 , , , ,

[Click here for a PDF of this post with nicer formatting]

In [1] it is claimed in an Aharonov-Bohm discussion that a Lagrangian modification to include electromagnetism is

\begin{equation}\label{eqn:magneticLorentzForceLagrangian:20}
\LL \rightarrow \LL + \frac{e}{c} \Bv \cdot \BA.
\end{equation}

That can’t be the full Lagrangian since there is no \( \phi \) term, so what exactly do we get?

If you have somehow, like I did, forgot the exact form of the Euler-Lagrange equations (i.e. where do the dots go), then the derivation of those equations can come to your rescue. The starting point is the action

\begin{equation}\label{eqn:magneticLorentzForceLagrangian:40}
S = \int \LL(x, \xdot, t) dt,
\end{equation}

where the end points of the integral are fixed, and we assume we have no variation at the end points. The variational calculation is

\begin{equation}\label{eqn:magneticLorentzForceLagrangian:60}
\begin{aligned}
\delta S
&= \int \delta \LL(x, \xdot, t) dt \\
&= \int \lr{ \PD{x}{\LL} \delta x + \PD{\xdot}{\LL} \delta \xdot } dt \\
&= \int \lr{ \PD{x}{\LL} \delta x + \PD{\xdot}{\LL} \delta \ddt{x} } dt \\
&= \int \lr{ \PD{x}{\LL} – \ddt{}\lr{\PD{\xdot}{\LL}} } \delta x dt
+ \delta x \PD{\xdot}{\LL}.
\end{aligned}
\end{equation}

The boundary term is killed after evaluation at the end points where the variation is zero. For the result to hold for all variations \( \delta x \), we must have

\begin{equation}\label{eqn:magneticLorentzForceLagrangian:80}
\boxed{
\PD{x}{\LL} = \ddt{}\lr{\PD{\xdot}{\LL}}.
}
\end{equation}

Now lets apply this to the Lagrangian at hand. For the position derivative we have

\begin{equation}\label{eqn:magneticLorentzForceLagrangian:100}
\PD{x_i}{\LL}
=
\frac{e}{c} v_j \PD{x_i}{A_j}.
\end{equation}

For the canonical momentum term, assuming \( \BA = \BA(\Bx) \) we have

\begin{equation}\label{eqn:magneticLorentzForceLagrangian:120}
\begin{aligned}
\ddt{} \PD{\xdot_i}{\LL}
&=
\ddt{}
\lr{ m \xdot_i
+
\frac{e}{c} A_i
} \\
&=
m \ddot{x}_i
+
\frac{e}{c}
\ddt{A_i} \\
&=
m \ddot{x}_i
+
\frac{e}{c}
\PD{x_j}{A_i} \frac{dx_j}{dt}.
\end{aligned}
\end{equation}

Assembling the results, we’ve got

\begin{equation}\label{eqn:magneticLorentzForceLagrangian:140}
\begin{aligned}
0
&=
\ddt{} \PD{\xdot_i}{\LL}
–
\PD{x_i}{\LL} \\
&=
m \ddot{x}_i
+
\frac{e}{c}
\PD{x_j}{A_i} \frac{dx_j}{dt}
–
\frac{e}{c} v_j \PD{x_i}{A_j},
\end{aligned}
\end{equation}

or
\begin{equation}\label{eqn:magneticLorentzForceLagrangian:160}
\begin{aligned}
m \ddot{x}_i
&=
\frac{e}{c} v_j \PD{x_i}{A_j}
–
\frac{e}{c}
\PD{x_j}{A_i} v_j \\
&=
\frac{e}{c} v_j
\lr{
\PD{x_i}{A_j}
–
\PD{x_j}{A_i}
} \\
&=
\frac{e}{c} v_j B_k \epsilon_{i j k}.
\end{aligned}
\end{equation}

In vector form that is

\begin{equation}\label{eqn:magneticLorentzForceLagrangian:180}
m \ddot{\Bx}
=
\frac{e}{c} \Bv \cross \BB.
\end{equation}

So, we get the magnetic term of the Lorentz force. Also note that this shows the Lagrangian (and the end result), was not in SI units. The \( 1/c \) term would have to be dropped for SI.

References

[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.