[Click here for a PDF of this post with nicer formatting]
Conservation of the field momentum.
This is a follow up to the unanswered questions I had yesterday related to the apparent time dependent terms in the previous expansion of \( P^i \) for a scalar field.
It turns out that examining the reasons that we can say that the field momentum is conserved also sheds some light on the question. \( P^i \) is not an a-priori conserved quantity, but we may use the charge conservation argument to justify this despite it not having a four-vector nature (i.e. with zero four divergence.)
The momentum \( P^i \) that we have defined is related to the conserved quantity \( T^{0\mu} \), the energy-momentum tensor, which satisfies \( 0 = \partial_\mu T^{0\mu} \) by Noether’s theorem (this was the conserved quantity associated with a spacetime translation.)
That tensor was
\begin{equation}\label{eqn:momentum:120}
T^{\mu\nu} = \partial^\mu \phi \partial^\nu \phi – g^{\mu\nu} \LL,
\end{equation}
and can be used to define the momenta
\begin{equation}\label{eqn:momentum:140}
\begin{aligned}
\int d^3 x T^{0k}
&= \int d^3 x \partial^0 \phi \partial^k \phi \\
&= \int d^3 x \pi \partial^k \phi.
\end{aligned}
\end{equation}
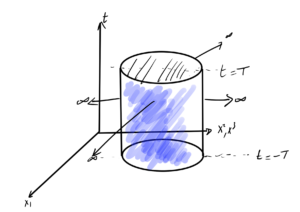
Charge \( Q^i = \int d^3 x j^0 \) was conserved with respect to a limiting surface argument, and we can make a similar “beer can integral” argument for \( P^i \), integrating over a large time interval \( t \in [-T, T] \) as sketched in fig. 1. That is
\begin{equation}\label{eqn:momentum:160}
\begin{aligned}
0
&=
\partial_\mu \int d^4 x T^{0\mu} \\
&=
\partial_0 \int d^4 x T^{00}
+
\partial_k \int d^4 x T^{0k} \\
&=
\partial_0 \int_{-T}^T dt \int d^3 x T^{00}
+
\partial_k \int_{-T}^T dt \int d^3 x T^{0k} \\
&=
\partial_0 \int_{-T}^T dt \int d^3 x T^{00}
+
\partial_k \int_{-T}^T dt
\inv{2} \int \frac{d^3 p }{(2 \pi)^3} p^k
\lr{
a_\Bp^\dagger a_\Bp
+ a_\Bp a_\Bp^\dagger
– a_\Bp a_{-\Bp} e^{- 2 i \omega_\Bp t}
– a_\Bp^\dagger a_{-\Bp}^\dagger e^{2 i \omega_\Bp t}
} \\
&=
\int d^3 x \evalrange{T^{00}}{-T}{T}
+
T \partial_k
\int \frac{d^3 p }{(2 \pi)^3} p^k
\lr{
a_\Bp^\dagger a_\Bp
+ a_\Bp a_\Bp^\dagger
}
-\inv{2}
\partial_k \int_{-T}^T dt
\int \frac{d^3 p }{(2 \pi)^3} p^k
\lr{
a_\Bp a_{-\Bp} e^{- 2 i \omega_\Bp t}
+ a_\Bp^\dagger a_{-\Bp}^\dagger e^{2 i \omega_\Bp t}
}.
\end{aligned}
\end{equation}
The first integral can be said to vanish if the field energy goes to zero at the time boundaries, and the last integral reduces to
\begin{equation}\label{eqn:momentum:180}
\begin{aligned}
-\inv{2}
\partial_k \int_{-T}^T dt
\int \frac{d^3 p }{(2 \pi)^3} p^k
\lr{
a_\Bp a_{-\Bp} e^{- 2 i \omega_\Bp t}
+ a_\Bp^\dagger a_{-\Bp}^\dagger e^{2 i \omega_\Bp t}
}
&=
-\int \frac{d^3 p }{2 (2 \pi)^3} p^k
\lr{
a_\Bp a_{-\Bp} \frac{\sin( -2 \omega_\Bp T )}{-2 \omega_\Bp}
+ a_\Bp^\dagger a_{-\Bp}^\dagger \frac{\sin( 2 \omega_\Bp T )}{2 \omega_\Bp}
} \\
&=
-\int \frac{d^3 p }{2 (2 \pi)^3} p^k
\lr{
a_\Bp a_{-\Bp} + a_\Bp^\dagger a_{-\Bp}^\dagger
}
\frac{\sin( 2 \omega_\Bp T )}{2 \omega_\Bp}
.
\end{aligned}
\end{equation}
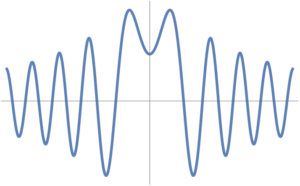
The \( \sin \) term can be interpretted as a sinc like function of \( \omega_\Bp \) which vanishes for large \( \Bp \). It’s not entirely sinc like for a massive field as \( \omega_\Bp = \sqrt{ \Bp^2 + m^2 } \), which never hits zero, as shown in fig. 2.
Vanishing for large \( \Bp \) doesn’t help the whole integral vanish, but we can resort to the Riemann-Lebesque lemma [1] instead and interpret this integral as one with a plain old high frequency oscillation that is presumed to vanish (i.e. the rest is well behaved enough that it can be labelled as \( L_1 \) integrable.)
We see that only the non-time dependent portion of \( \mathbf{P} \) matters from a conserved quantity point of view, and having killed off all the time dependent terms, we are left with a conservation relationship for the momenta \( \spacegrad \cdot \BP = 0 \), where \( \BP \) in normal order is just
\begin{equation}\label{eqn:momentum:200}
: \BP : = \int \frac{d^3 p}{(2 \pi)^3} \Bp a_\Bp^\dagger a_\Bp.
\end{equation}
References
[1] Wikipedia contributors. Riemann-lebesgue lemma — Wikipedia, the free encyclopedia, 2018. URL https://en.wikipedia.org/w/index.php?title=Riemann%E2%80%93Lebesgue_lemma&oldid=856778941. [Online; accessed 29-October-2018].