This post is a synopsis of the material from the second last lecture of QFT I. I missed that class, but worked from notes kindly provided by Emily Tyhurst, and Stefan Divic, filling in enough details that it made sense to me.
[Click here for an unabrided PDF of my full notes on this day’s lecture material.]
Topics covered include
- The Hamiltonian action on single particle states showed that the Hamiltonian was an energy eigenoperator
\begin{equation}\label{eqn:qftLecture22:140}
H \ket{\Bp, r}
=
\omega_\Bp \ket{\Bp, r}.
\end{equation} - The conserved Noether current and charge for spatial translations, the momentum operator, was found to be
\begin{equation}\label{eqn:momentumDirac:260}
\BP =
\int d^3 x
\Psi^\dagger (-i \spacegrad) \Psi,
\end{equation}
which could be written in creation and anhillation operator form as
\begin{equation}\label{eqn:momentumDirac:261}
\BP = \sum_{s = 1}^2
\int \frac{d^3 q}{(2\pi)^3} \Bp \lr{
a_\Bp^{s\dagger}
a_\Bp^{s}
+
b_\Bp^{s\dagger}
b_\Bp^{s}
}.
\end{equation}
Single particle states were found to be the eigenvectors of this operator, with momentum eigenvalues
\begin{equation}\label{eqn:momentumDirac:262}
\BP a_\Bq^{s\dagger} \ket{0} = \Bq (a_\Bq^{s\dagger} \ket{0}).
\end{equation} - The conserved Noether current and charge for a rotation was found. That charge is
\begin{equation}\label{eqn:qftLecture22:920}
\BJ = \int d^3 x \Psi^\dagger(x) \lr{ \underbrace{\Bx \cross (-i \spacegrad)}_{\text{orbital angular momentum}} + \inv{2} \underbrace{\mathbf{1} \otimes \Bsigma}_{\text{spin angular momentum}} } \Psi,
\end{equation}
where
\begin{equation}\label{eqn:qftLecture22:260}
\mathbf{1} \otimes \Bsigma =
\begin{bmatrix}
\Bsigma & 0 \\
0 & \Bsigma
\end{bmatrix},
\end{equation}
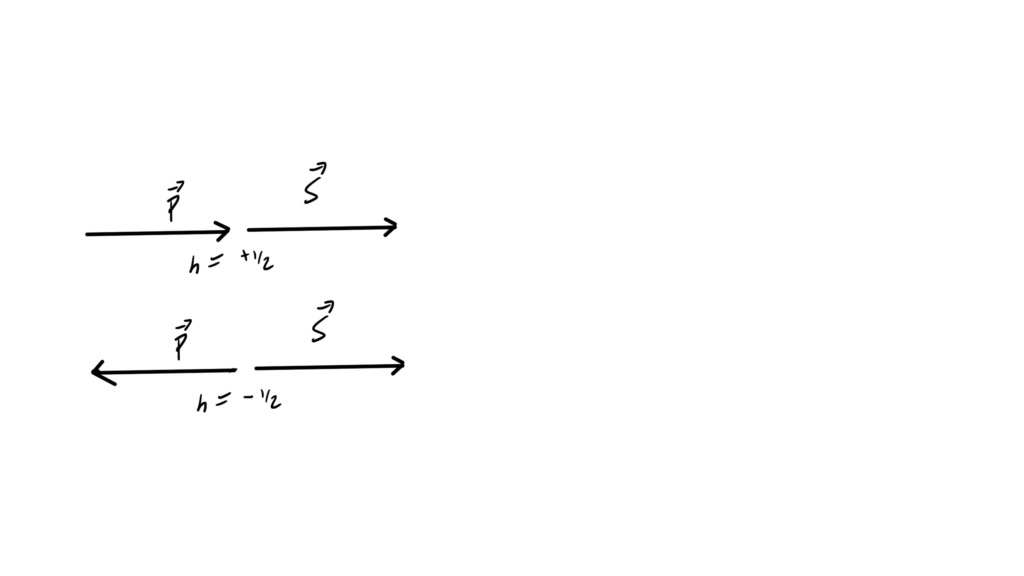
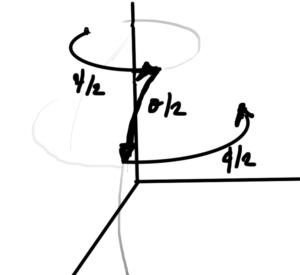
which has distinct orbital and spin angular momentum components. Unlike NRQM, we see both types of angular momentum as components of a single operator. It is argued in [3] that for a particle at rest the single particle state is an eigenvector of this operator, with eigenvalues \( \pm 1/2 \) — the Fermion spin eigenvalues! - We examined two \( U(1) \) global symmetries. The Noether charge for the “vector” \( U(1) \) symmetry is
\begin{equation}\label{eqn:qftLecture22:380}
Q
=
\int \frac{d^3 q}{(2\pi)^3} \sum_{s = 1}^2
\lr{
a_\Bp^{s \dagger} a_\Bp^s
–
b_\Bp^{s \dagger}
b_\Bp^s
},
\end{equation}
This charge operator characterizes the \( a, b \) operators. \( a \) particles have charge \( +1 \), and \( b \) particles have charge \( -1 \), or vice-versa depending on convention. We call \( a \) the operator for the electron, and \( b \) the operator for the positron. - CPT (Charge-Parity-TimeReversal) symmetries were also mentioned, but not covered in class. We were pointed to [2], [3], [4] to start studying that topic.
References
[1] C. Doran and A.N. Lasenby. Geometric algebra for physicists. Cambridge University Press New York, Cambridge, UK, 1st edition, 2003.
[2] Dr. Michael Luke. Quantum Field Theory., 2011. URL https://www.physics.utoronto.ca/~luke/PHY2403F/References_files/lecturenotes.pdf. [Online; accessed 05-Dec-2018].
[3] Michael E Peskin and Daniel V Schroeder. An introduction to Quantum Field Theory. Westview, 1995.
[4] Dr. David Tong. Quantum Field Theory. URL http://www.damtp.cam.ac.uk/user/tong/qft.html.