discrete time system

Stability of discretized linear differential equations

November 17, 2014 ece1254 , , , ,

[Click here for a PDF of this post with nicer formatting]

In class today was a highlight of stability methods for linear multistep methods. To motivate the methods used, it is helpful to take a step back and review stability concepts for LDE systems.

By way of example, consider a second order LDE homogeneous system defined by

\begin{equation}\label{eqn:stabilityLDEandDiscreteTime:20}
\frac{d^2 x}{dt^2} + 3 \frac{dx}{dt} + 2 = 0.
\end{equation}

Such a system can be solved by assuming an exponential solution, say

\begin{equation}\label{eqn:stabilityLDEandDiscreteTime:40}
x(t) = e^{s t}.
\end{equation}

Substitution gives

\begin{equation}\label{eqn:stabilityLDEandDiscreteTime:60}
e^{st} \lr{ s^2 + 3 s + 2 } = 0,
\end{equation}

The polynomial part of this equation, the characteristic equation has roots \( s = -2, -1 \).

The general solution of \ref{eqn:stabilityLDEandDiscreteTime:20} is formed by a superposition of solutions for each value of \(s\)

\begin{equation}\label{eqn:stabilityLDEandDiscreteTime:80}
x(t) = a e^{-2 t} + b e^{-t}.
\end{equation}

Independent of any selection of the superposition constants \( a, b \), this function will not blow up as \( t \rightarrow \infty \).

This “stability” is due to the fact that both of the characteristic equation roots lie in the left hand Argand plane.

Now consider a discretized form of this LDE. This will have the form

\begin{equation}\label{eqn:stabilityLDEandDiscreteTime:100}
\begin{aligned}
0 &=
\inv{\lr{\Delta t}^2}
\lr{ x_{n+2} – 2 x_{n-1} + x_n } + \frac{3}{\Delta t} \lr{ x_{n+1} – x_n } + 2
x_n \\
&=
x_{n+2} \lr{
\inv{\lr{\Delta t}^2}
}
+
x_{n+1} \lr{
\frac{3}{\Delta t}
-\frac{2}{\lr{\Delta t}^2}
}
+
x_{n} \lr{
\frac{1}{\lr{\Delta t}^2}
-\frac{3}{\Delta t}
+ 2
},
\end{aligned}
\end{equation}

or

\begin{equation}\label{eqn:stabilityLDEandDiscreteTime:220}
0
=
x_{n+2}
+
x_{n+1} \lr{
3 \Delta t – 2
}
+
x_{n} \lr{
1 – 3 \Delta t + 2 \lr{ \Delta t}^2
}.
\end{equation}

Note that after discretization, each subsequent index corresponds to a time shift. Also observe that the coefficients of this discretized equation are dependent on the discretization interval size \( \Delta t \). If the specifics of those coefficients are ignored, a general form with the following structure can be observed

\begin{equation}\label{eqn:stabilityLDEandDiscreteTime:120}
0 =
x_{n+2} \gamma_0
+
x_{n+1} \gamma_1
+
x_{n} \gamma_2.
\end{equation}

It turns out that, much like the LDE solution by characteristic polynomial, it is possible to attack this problem by assuming a solution of the form

\begin{equation}\label{eqn:stabilityLDEandDiscreteTime:140}
x_n = C z^n.
\end{equation}

A time shift index change \( x_n \rightarrow x_{n+1} \) results in a power adjustment in this assumed solution. This substitution applied to \ref{eqn:stabilityLDEandDiscreteTime:120} yields

\begin{equation}\label{eqn:stabilityLDEandDiscreteTime:160}
0 =
C z^n
\lr{
z^{2} \gamma_0
+
z \gamma_1
+
1 \gamma_2
},
\end{equation}

Suppose that this polynomial has roots \( z \in \{z_1, z_2\} \). A superposition, such as

\begin{equation}\label{eqn:stabilityLDEandDiscreteTime:180}
x_n = a z_1^n + b z_2^n,
\end{equation}

will also be a solution since insertion of this into the RHS of \ref{eqn:stabilityLDEandDiscreteTime:120} yields

\begin{equation}\label{eqn:stabilityLDEandDiscreteTime:200}
a z_1^n
\lr{
z_1^{2} \gamma_0
+
z_1 \gamma_1
+
\gamma_2
}
+
b
z_2^n
\lr{
z_2^{2} \gamma_0
+
z_2 \gamma_1
+
\gamma_2
}
=
a z_1^n \times 0
+b z_2^n \times 0.
\end{equation}

The zero equality follows since \( z_1, z_2 \) are both roots of the characteristic equation for this discretized LDE.
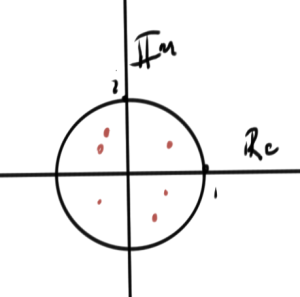
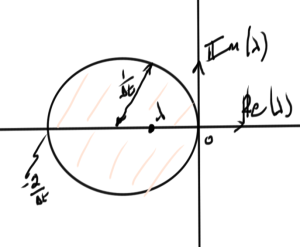
In the discrete \( z \) domain stability requires that the roots satisfy the bound \( \Abs{z} < 1 \), a different stability criteria than in the continuous domain. In fact, there is no a-priori guarantee that stability in the continuous domain will imply stability in the discretized domain. Let's plot those z-domain roots for this example LDE, using \( \Delta t \in \{ 1/2, 1, 2 \} \). The respective characteristic polynomials are \begin{equation}\label{eqn:stabilityLDEandDiscreteTime:260} 0 = z^2 - \inv{2} z = z \lr{ z - \inv{2} } \end{equation} \begin{equation}\label{eqn:stabilityLDEandDiscreteTime:240} 0 = z^2 + z = z\lr{ z + 1 } \end{equation} \begin{equation}\label{eqn:stabilityLDEandDiscreteTime:280} 0 = z^2 + 4 z + 3 = (z + 3)(z + 1). \end{equation} These have respective roots \begin{equation}\label{eqn:stabilityLDEandDiscreteTime:300} z = 0, \inv{2} \end{equation} \begin{equation}\label{eqn:stabilityLDEandDiscreteTime:320} z = 0, -1 \end{equation} \begin{equation}\label{eqn:stabilityLDEandDiscreteTime:340} z = -1, -3 \end{equation} Only the first discretization of these three yields stable solutions in the z domain, although it appears that \( \Delta t = 1 \) is right on the boundary.

ECE1254H Modeling of Multiphysics Systems. Lecture 16: LMS systems and stability. Taught by Prof. Piero Triverio

November 17, 2014 ece1254 , , ,

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

Residual for LMS methods

Mostly on slides:

12_ODS.pdf

Residual is illustrated in fig. 1, assuming that the iterative method was accurate until \( t_{n} \)

lecture16Fig1

fig. 1. Residual illustrated

 

Summary

  • [FE]: \( R_{n+1} \sim \lr{ \Delta t}^2 \). This is of order \( p = 1 \).
  • [BE]: \( R_{n+1} \sim \lr{ \Delta t}^2 \). This is of order \( p = 1 \).
  • [TR]: \( R_{n+1} \sim \lr{ \Delta t}^3 \). This is of order \( p = 2 \).
  • [BESTE]: \( R_{n+1} \sim \lr{ \Delta t}^4 \). This is of order \( p = 3 \).

Global error estimate

Suppose \( t \in [0, 1] s \), with \( N = 1/{\Delta t} \) intervals. For a method with local error of order \( R_{n+1} \sim \lr{ \Delta t}^2 \) the global error is approximately \( N R_{n+1} \sim \Delta t \).

Stability

Recall that a linear multistep method (LMS) was a system of the form

\begin{equation}\label{eqn:multiphysicsL16:20}
\sum_{j=-1}^{k-1} \alpha_j x_{n-j} = \Delta t \sum_{j=-1}^{k-1} \beta_j f( x_{n-j}, t_{n-j} )
\end{equation}

Consider a one dimensional test problem

\begin{equation}\label{eqn:multiphysicsL16:40}
\dot{x}(t) = \lambda x(t)
\end{equation}

where as in fig. 2, \( \Re(\lambda) < 0 \) is assumed to ensure stability.

lecture16Fig2

fig. 2. Stable system

 

Linear stability theory can be thought of as asking the question: “Is the solution of \ref{eqn:multiphysicsL16:40} computed by my LMS method also stable?”

Application of \ref{eqn:multiphysicsL16:20} to \ref{eqn:multiphysicsL16:40} gives

\begin{equation}\label{eqn:multiphysicsL16:60}
\sum_{j=-1}^{k-1} \alpha_j x_{n-j} = \Delta t \sum_{j=-1}^{k-1} \beta_j \lambda x_{n-j},
\end{equation}

or
\begin{equation}\label{eqn:multiphysicsL16:80}
\sum_{j=-1}^{k-1} \lr{ \alpha_j – \Delta \beta_j \lambda }
x_{n-j} = 0.
\end{equation}

With

\begin{equation}\label{eqn:multiphysicsL16:100}
\gamma_j = \alpha_j – \Delta \beta_j \lambda,
\end{equation}

this expands to
\begin{equation}\label{eqn:multiphysicsL16:120}
\gamma_{-1} x_{n+1}
+
\gamma_{0} x_{n}
+
\gamma_{1} x_{n-1}
+
\cdots
+
\gamma_{k-1} x_{n-k} .
\end{equation}

This can be seen as a

  • discrete time system
  • FIR filter

The numerical solution \( x_n \) will be stable if \ref{eqn:multiphysicsL16:120} is stable.

A characteristic equation associated with \ref{eqn:multiphysicsL16:120} can be defined as

\begin{equation}\label{eqn:multiphysicsL16:140}
\gamma_{-1} z^k
+
\gamma_{0} z^{k-1}
+
\gamma_{1} z^{k-2}
+
\cdots
+
\gamma_{k-1} = 0.
\end{equation}

This is a polynomial with roots \( z_n \) (poles). This is stable if the poles satisfy \( \Abs{z_n} < 1 \), as illustrated in fig. 3

lecture16Fig3

Stability

 

Observe that the \( \gamma’s \) are dependent on \( \Delta t \).

FIXME: There’s a lot of handwaving here that could use more strict justification. Check if the text covers this in more detail.

Example: Forward Euler stability

For \( k = 1 \) step.

\begin{equation}\label{eqn:multiphysicsL16:180}
x_{n+1} – x_n = \Delta t f( x_n, t_n ),
\end{equation}

the coefficients are \( \alpha_{-1} = 1, \alpha_0 = -1, \beta_{-1} = 0, \beta_0 =1 \). For the simple function above

\begin{equation}\label{eqn:multiphysicsL16:200}
\gamma_{-1} = \alpha_{-1} – \Delta t \lambda \beta_{-1} = 1
\end{equation}
\begin{equation}\label{eqn:multiphysicsL16:220}
\gamma_{0} = \alpha_{0} – \Delta t \lambda \beta_{0} = -1 – \Delta t \lambda.
\end{equation}

The stability polynomial is

\begin{equation}\label{eqn:multiphysicsL16:240}
1 z + \lr{ -1 – \Delta t \lambda} = 0,
\end{equation}

or

\begin{equation}\label{eqn:multiphysicsL16:260}
\boxed{
z = 1 + \delta t \lambda.
}
\end{equation}

This is the root, or pole.

For stability we must have

\begin{equation}\label{eqn:multiphysicsL16:280}
\Abs{ 1 + \Delta t \lambda } < 1,
\end{equation}

or
\begin{equation}\label{eqn:multiphysicsL16:300}
\Abs{ \lambda – \lr{ -\inv{\Delta t} } } < \inv{\Delta t},
\end{equation}

This inequality is illustrated roughly in fig. 4.

lecture16Fig4

fig. 4. Stability region of FE

 

All poles of my system must be inside the stability region in order to get stable \( \gamma \).