matrix element

PHY2403H Quantum Field Theory. Lecture 23: QED and QCD interaction Lagrangian, Feynman propagator and rules for Fermions, hadron pair production, scattering cross section, quark pair production. Taught by Prof. Erich Poppitz

December 26, 2018 phy2403 , , , , , , , , , , , , , , , ,

Here is a link to [a PDF with my notes for the final QFT I lecture.] That lecture followed [1] section 5.1 fairly closely (filling in some details, leaving out some others.)

This lecture

  • Introduced an interaction Lagrangian with QED and QCD interaction terms
    \begin{equation*}
    \LL_{\text{QED}}
    =
    – \inv{4} F_{\mu\nu} F^{\mu\nu}
    +
    \overline{\Psi}_e \lr{ i \gamma^\mu \partial_\mu – m } \Psi_e
    –
    e \overline{\Psi}_e \gamma_\mu \Psi_e A^\mu
    +
    \overline{\Psi}_\mu \lr{ i \gamma^\mu \partial_\mu – m } \Psi_\mu
    –
    e \overline{\Psi}_\mu \gamma_\mu \Psi_\mu A^\mu,
    \end{equation*}
    as well as the quark interaction Lagrangian
    \begin{equation*}
    \LL_{\text{quarks}} = \sum_q \overline{\Psi}_q \lr{ i \gamma^\mu – m_q } \Psi_q + e Q_q \overline{\Psi}_q \gamma^\nu \Psi_q A_\nu.
    \end{equation*}
  • The Feynman propagator for Fermions was calculated
    \begin{equation*}
    \expectation{ T( \Psi_\alpha(x) \Psi_\beta(x) }_0
    =
    \lr{ \gamma^\mu_{\alpha\beta} \partial_\mu^{(x)} + m } D_F(x – y)
    =
    \int \frac{d^4 p}{(2 \pi)^4 } \frac{ i ( \gamma^\mu_{\alpha\beta} p_\mu + m ) }{p^2 – m^2 + i \epsilon} e^{-i p \cdot (x – y)}.
    \end{equation*}
  • We determined the Feynman rules for Fermion diagram nodes and edges.
    The Feynman propagator for Fermions is
    \begin{equation*}
    \frac{ i \lr{ \gamma^\mu p_\mu + m } }{p^2 – m^2 + i \epsilon},
    \end{equation*}
    whereas the photon propagator is
    \begin{equation*}
    \expectation{ A_\mu A_\nu } = -i \frac{g_{\mu\nu}}{q^2 + i \epsilon}.
    \end{equation*}

  • Muon pair production

    We then studied muon pair production in detail, and determined the form of the scattering matrix element
    \begin{equation*}
    i M
    =
    i \frac{e^2}{q^2}
    \overline{v}^{s’}(p’) \gamma^\rho u^s(p)
    \overline{u}^r(k) \gamma_\rho v^{r’}(k’),
    \end{equation*}
    where the \( (2 \pi)^4 \delta^4(…) \) term hasn’t been made explicit, and detemined that the average of its square over all input and output polarization (spin) states was
    \begin{equation*}
    \inv{4} \sum_{ss’, rr’} \Abs{M}^2
    =
    \frac{e^4}{4 q^4}
    \textrm{tr}{ \lr{
    \lr{ \gamma^\alpha {k’}_\alpha – m_\mu }
    \gamma_\nu
    \lr{ \gamma^\beta {k}_\beta + m_\mu }
    \gamma_\mu
    }}
    \times
    \textrm{tr}{ \lr{
    \lr{ \gamma^\kappa {p}_\kappa + m_e }
    \gamma^\nu
    \lr{ \gamma^\rho {p’}_\rho – m_e }
    \gamma^\mu
    }}.
    \end{equation*}.
    In the CM frame (neglecting the electron mass, which is small relative to the muon mass), this reduced to
    \begin{equation*}
    \inv{4} \sum_{\text{spins}} \Abs{M}^2
    =
    \frac{8 e^4}{q^4}
    \lr{
    p \cdot k’ p’ \cdot k
    + p \cdot k p’ \cdot k’
    + p \cdot p’ m_\mu^2
    }.
    \end{equation*}

  • We computed the differential cross section
    \begin{equation*}
    {\frac{d\sigma}{d\Omega}}_{\text{CM}}
    =
    \frac{\alpha^2}{4 E_{\text{CM}}^2 }
    \sqrt{ 1 – \frac{m_\mu^2}{E^2} }
    \lr{
    1 + \frac{m_\mu^2}{E^2}
    + \lr{ 1 – \frac{m_\mu^2}{E^2} } \cos^2\theta
    },
    \end{equation*}
    and the total cross section
    \begin{equation*}
    \sigma_{\text{total}}
    =
    \frac{4 \pi \alpha^2}{3 E_{\text{CM}}^2 }
    \sqrt{ 1 – \frac{m_\mu^2}{E^2} }
    \lr{
    1 + \inv{2} \frac{m_\mu^2}{E^2}
    },
    \end{equation*}
    and compared that to the cross section that we was determined with the dimensional analysis handwaving at the start of the course.
  • We finished off with a quick discussion of quark pair production, and how some of the calculations we performed for muon pair production can be used to measure and validate the intermediate quark states that were theorized as carriers of the strong force.

References

[1] Michael E Peskin and Daniel V Schroeder. An introduction to Quantum Field Theory. Westview, 1995.

PHY1520H Graduate Quantum Mechanics. Lecture 1: Lighting review. Taught by Prof. Arun Paramekanti

September 17, 2015 phy1520 , , , , , , , , , , , , , ,

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

These are notes for the UofT course PHY1520, Graduate Quantum Mechanics, taught by Prof. Paramekanti, covering [1] chap. 1 content.

Classical mechanics

We’ll be talking about one body physics for most of this course. In classical mechanics we can figure out the particle trajectories using both of \( (\Br, \Bp \), where

\begin{equation}\label{eqn:qmLecture1:20}
\begin{aligned}
\ddt{\Br} &= \inv{m} \Bp \\
\ddt{\Bp} &= \spacegrad V
\end{aligned}
\end{equation}

A two dimensional phase space as sketched in fig. 1 shows the trajectory of a point particle subject to some equations of motion

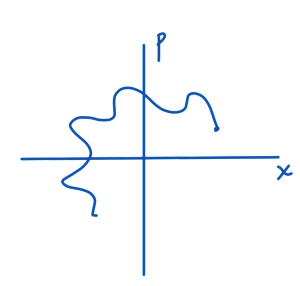
lectureOnePhaseSpaceClassicalFig1

fig. 1. One dimensional classical phase space example

Quantum mechanics

For this lecture, we’ll work with natural units, setting

\begin{equation}\label{eqn:qmLecture1:480}
\boxed{
\Hbar = 1.
}
\end{equation}

In QM we are no longer allowed to think of position and momentum, but have to start asking about state vectors \( \ket{\Psi} \).

We’ll consider the state vector with respect to some basis, for example, in a position basis, we write

\begin{equation}\label{eqn:qmLecture1:40}
\braket{ x }{\Psi } = \Psi(x),
\end{equation}

a complex numbered “wave function”, the probability amplitude for a particle in \( \ket{\Psi} \) to be in the vicinity of \( x \).

We could also consider the state in a momentum basis

\begin{equation}\label{eqn:qmLecture1:60}
\braket{ p }{\Psi } = \Psi(p),
\end{equation}

a probability amplitude with respect to momentum \( p \).

More precisely,

\begin{equation}\label{eqn:qmLecture1:80}
\Abs{\Psi(x)}^2 dx \ge 0
\end{equation}

is the probability of finding the particle in the range \( (x, x + dx ) \). To have meaning as a probability, we require

\begin{equation}\label{eqn:qmLecture1:100}
\int_{-\infty}^\infty \Abs{\Psi(x)}^2 dx = 1.
\end{equation}

The average position can be calculated using this probability density function. For example

\begin{equation}\label{eqn:qmLecture1:120}
\expectation{x} = \int_{-\infty}^\infty \Abs{\Psi(x)}^2 x dx,
\end{equation}

or
\begin{equation}\label{eqn:qmLecture1:140}
\expectation{f(x)} = \int_{-\infty}^\infty \Abs{\Psi(x)}^2 f(x) dx.
\end{equation}

Similarly, calculation of an average of a function of momentum can be expressed as

\begin{equation}\label{eqn:qmLecture1:160}
\expectation{f(p)} = \int_{-\infty}^\infty \Abs{\Psi(p)}^2 f(p) dp.
\end{equation}

Transformation from a position to momentum basis

We have a problem, if we which to compute an average in momentum space such as \( \expectation{p} \), when given a wavefunction \( \Psi(x) \).

How do we convert

\begin{equation}\label{eqn:qmLecture1:180}
\Psi(p)
\stackrel{?}{\leftrightarrow}
\Psi(x),
\end{equation}

or equivalently
\begin{equation}\label{eqn:qmLecture1:200}
\braket{p}{\Psi}
\stackrel{?}{\leftrightarrow}
\braket{x}{\Psi}.
\end{equation}

Such a conversion can be performed by virtue of an the assumption that we have a complete orthonormal basis, for which we can introduce identity operations such as

\begin{equation}\label{eqn:qmLecture1:220}
\int_{-\infty}^\infty dp \ket{p}\bra{p} = 1,
\end{equation}

or
\begin{equation}\label{eqn:qmLecture1:240}
\int_{-\infty}^\infty dx \ket{x}\bra{x} = 1
\end{equation}

Some interpretations:

  1. \( \ket{x_0} \leftrightarrow \text{sits at} x = x_0 \)
  2. \( \braket{x}{x’} \leftrightarrow \delta(x – x’) \)
  3. \( \braket{p}{p’} \leftrightarrow \delta(p – p’) \)
  4. \( \braket{x}{p’} = \frac{e^{i p x}}{\sqrt{V}} \), where \( V \) is the volume of the box containing the particle. We’ll define the appropriate normalization for an infinite box volume later.

The delta function interpretation of the braket \( \braket{p}{p’} \) justifies the identity operator, since we recover any state in the basis when operating with it. For example, in momentum space

\begin{equation}\label{eqn:qmLecture1:260}
\begin{aligned}
1 \ket{p}
&=
\lr{ \int_{-\infty}^\infty dp’
\ket{p’}\bra{p’} }
\ket{p} \\
&=
\int_{-\infty}^\infty dp’
\ket{p’}
\braket{p’}{p} \\
&=
\int_{-\infty}^\infty dp’
\ket{p’}
\delta(p – p’) \\
&=
\ket{p}.
\end{aligned}
\end{equation}

This also the determination of an integral operator representation for the delta function

\begin{equation}\label{eqn:qmLecture1:500}
\begin{aligned}
\delta(x – x’)
&=
\braket{x}{x’} \\
&=
\int dp \braket{x}{p} \braket{p}{x’} \\
&=
\inv{V} \int dp e^{i p x} e^{-i p x’},
\end{aligned}
\end{equation}

or

\begin{equation}\label{eqn:qmLecture1:520}
\delta(x – x’)
=
\inv{V} \int dp e^{i p (x- x’)}.
\end{equation}

Here we used the fact that \( \braket{p}{x} = \braket{x}{p}^\conj \).

FIXME: do we have a justification for that conjugation with what was defined here so far?

The conversion from a position basis to momentum space is now possible

\begin{equation}\label{eqn:qmLecture1:280}
\begin{aligned}
\braket{p}{\Psi}
&= \Psi(p) \\
&= \int_{-\infty}^\infty \braket{p}{x} \braket{x}{\Psi} dx \\
&= \int_{-\infty}^\infty \frac{e^{-ip x}}{\sqrt{V}} \Psi(x) dx.
\end{aligned}
\end{equation}

The momentum space to position space conversion can be written as

\begin{equation}\label{eqn:qmLecture1:300}
\Psi(x)
= \int_{-\infty}^\infty \frac{e^{ip x}}{\sqrt{V}} \Psi(p) dp.
\end{equation}

Now we can go back and figure out the an expectation

\begin{equation}\label{eqn:qmLecture1:320}
\begin{aligned}
\expectation{p}
&=
\int \Psi^\conj(p) \Psi(p) p d p \\
&=
\int dp
\lr{
\int_{-\infty}^\infty \frac{e^{ip x}}{\sqrt{V}} \Psi^\conj(x) dx
}
\lr{
\int_{-\infty}^\infty \frac{e^{-ip x’}}{\sqrt{V}} \Psi(x’) dx’
}
p \\
&=\int dp dx dx’
\Psi^\conj(x)
\inv{V} e^{ip (x-x’)} \Psi(x’) p \\
&=
\int dp dx dx’
\Psi^\conj(x)
\inv{V} \lr{ -i\PD{x}{e^{ip (x-x’)}} }\Psi(x’) \\
&=
\int dp dx
\Psi^\conj(x) \lr{ -i \PD{x}{} }
\inv{V} \int dx’ e^{ip (x-x’)} \Psi(x’) \\
&=
\int dx
\Psi^\conj(x) \lr{ -i \PD{x}{} }
\int dx’ \lr{ \inv{V} \int dp e^{ip (x-x’)} } \Psi(x’) \\
&=
\int dx
\Psi^\conj(x) \lr{ -i \PD{x}{} }
\int dx’ \delta(x – x’) \Psi(x’) \\
&=
\int dx
\Psi^\conj(x) \lr{ -i \PD{x}{} }
\Psi(x)
\end{aligned}
\end{equation}

Here we’ve essentially calculated the position space representation of the momentum operator, allowing identifications of the following form

\begin{equation}\label{eqn:qmLecture1:380}
p \leftrightarrow -i \PD{x}{}
\end{equation}
\begin{equation}\label{eqn:qmLecture1:400}
p^2 \leftrightarrow – \PDSq{x}{}.
\end{equation}

Alternate starting point.

Most of the above results followed from the claim that \( \braket{x}{p} = e^{i p x} \). Note that this position space representation of the momentum operator can also be taken as the starting point. Given that, the exponential representation of the position-momentum braket follows

\begin{equation}\label{eqn:qmLecture1:540}
\bra{x} P \ket{p}
=
-i \Hbar \PD{x}{} \braket{x}{p},
\end{equation}

but \( \bra{x} P \ket{p} = p \braket{x}{p} \), providing a differential equation for \( \braket{x}{p} \)

\begin{equation}\label{eqn:qmLecture1:560}
p \braket{x}{p} = -i \Hbar \PD{x}{} \braket{x}{p},
\end{equation}

with solution

\begin{equation}\label{eqn:qmLecture1:580}
i p x/\Hbar = \ln \braket{x}{p} + \text{const},
\end{equation}

or
\begin{equation}\label{eqn:qmLecture1:600}
\braket{x}{p} \propto e^{i p x/\Hbar}.
\end{equation}

Matrix interpretation

  1. Ket’s \( \ket{\Psi} \leftrightarrow \text{column vector} \)
  2. Bra’s \( \bra{\Psi} \leftrightarrow {(\text{row vector})}^\conj \)
  3. Operators \( \leftrightarrow \) matrices that act on vectors.

\begin{equation}\label{eqn:qmLecture1:420}
\hat{p} \ket{\Psi} \rightarrow \ket{\Psi’}
\end{equation}

Time evolution

For a state subject to the equations of motion given by the Hamiltonian operator \( \hat{H} \)

\begin{equation}\label{eqn:qmLecture1:440}
i \PD{t}{} \ket{\Psi} = \hat{H} \ket{\Psi},
\end{equation}

the time evolution is given by
\begin{equation}\label{eqn:qmLecture1:460}
\ket{\Psi(t)} = e^{-i \hat{H} t} \ket{\Psi(0)}.
\end{equation}

Incomplete information

We’ll need to introduce the concept of Density matrices. This will bring us to concepts like entanglement.

References

[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.

Momentum space representation of Schrodinger equation

September 2, 2015 phy1520 , , , , ,

[Click here for a PDF of this post with nicer formatting]

Question: momentum space representation of Schrodinger equation ([1] pr. 2.15)

Using

\begin{equation}\label{eqn:shoMomentumSpace:20}
\braket{x’}{p’} = \inv{\sqrt{2 \pi \Hbar}} e^{i p’ x’/\Hbar},
\end{equation}

show that

\begin{equation}\label{eqn:shoMomentumSpace:40}
\bra{p’} x \ket{\alpha} = i \Hbar \PD{p’}{} \braket{p’}{\alpha}.
\end{equation}

Use this to find the momentum space representation of the Schrodinger equation for the one dimensional SHO and the energy eigenfunctions in their momentum representation.

Answer

To expand the matrix element, introduce both momentum and position space identity operators

\begin{equation}\label{eqn:shoMomentumSpace:60}
\begin{aligned}
\bra{p’} x \ket{\alpha}
&=
\int dx’ dp” \braket{p’}{x’}\bra{x’}x \ket{p”}\braket{p”}{\alpha} \\
&=
\int dx’ dp” \braket{p’}{x’}x’\braket{x’}{p”}\braket{p”}{\alpha} \\
&=
\inv{2 \pi \Hbar}
\int dx’ dp” e^{-i p’ x’/\Hbar} x’ e^{i p” x’/\Hbar} \braket{p”}{\alpha} \\
&=
\inv{2 \pi \Hbar}
\int dx’ dp” x’ e^{i (p” – p’) x’/\Hbar} \braket{p”}{\alpha} \\
&=
\inv{2 \pi \Hbar}
\int dx’ dp” \frac{d}{dp”}\lr{ \frac{-i \Hbar} e^{i (p” – p’) x’/\Hbar} }
\braket{p”}{\alpha} \\
&=
i \Hbar
\int dp”
\lr{ \inv{2 \pi \Hbar}
\int dx’ e^{i (p” – p’) x’/\Hbar} } \frac{d}{dp”} \braket{p”}{\alpha} \\
&=
i \Hbar
\int dp” \delta(p”- p’)
\frac{d}{dp”} \braket{p”}{\alpha} \\
&=
i \Hbar
\frac{d}{dp’} \braket{p’}{\alpha}.
\end{aligned}
\end{equation}

Schrodinger’s equation for a time dependent state \( \ket{\alpha} = U(t) \ket{\alpha,0} \) is

\begin{equation}\label{eqn:shoMomentumSpace:80}
i \Hbar \PD{t}{} \ket{\alpha} = H \ket{\alpha},
\end{equation}

with the momentum representation

\begin{equation}\label{eqn:shoMomentumSpace:100}
i \Hbar \PD{t}{} \braket{p’}{\alpha} = \bra{p’} H \ket{\alpha}.
\end{equation}

Expansion of the Hamiltonian matrix element for a strictly spatial dependent potential \( V(x) \) gives

\begin{equation}\label{eqn:shoMomentumSpace:120}
\begin{aligned}
\bra{p’} H \ket{\alpha}
&=
\bra{p’} \lr{\frac{p^2}{2m} + V(x) } \ket{\alpha} \\
&=
\frac{(p’)^2}{2m}
+ \bra{p’} V(x) \ket{\alpha}.
\end{aligned}
\end{equation}

Assuming a Taylor representation of the potential \( V(x) = \sum c_k x^k \), we want to calculate

\begin{equation}\label{eqn:shoMomentumSpace:140}
\bra{p’} V(x) \ket{\alpha}
= \sum c_k \bra{p’} x^k \ket{\alpha}.
\end{equation}

With \( \ket{\alpha} = \ket{p”} \) \ref{eqn:shoMomentumSpace:40} provides the \( k = 1 \) term

\begin{equation}\label{eqn:shoMomentumSpace:160}
\begin{aligned}
\bra{p’} x \ket{p”}
&= i \Hbar \frac{d}{dp’} \braket{p’}{p”} \\
&= i \Hbar \frac{d}{dp’} \delta(p’ – p”),
\end{aligned}
\end{equation}

where it is implied here that the derivative is operating on not just the delta function, but on all else that follows.

Using this the higher powers of \( \bra{p’} x^k \ket{\alpha} \) can be found easily. For example for \( k = 2 \) we have

\begin{equation}\label{eqn:shoMomentumSpace:180}
\begin{aligned}
\bra{p’} x^2 \ket{\alpha}
&=
\int dp”
\bra{p’} x \ket{p”}\bra{p”} x \ket{\alpha} \\
&=
\int dp”
i \Hbar
\frac{d}{dp’} \delta(p’ – p”) i \Hbar \frac{d}{dp”} \braket{p”}{\alpha} \\
&=
\lr{ i \Hbar }^2 \frac{d^2}{d(p’)^2} \braket{p’}{\alpha}.
\end{aligned}
\end{equation}

This means that the potential matrix element is

\begin{equation}\label{eqn:shoMomentumSpace:200}
\begin{aligned}
\bra{p’} V(x) \ket{\alpha}
&=
\sum c_k \lr{ i \Hbar \frac{d}{dp’} }^k \braket{p’}{\alpha} \\
&= V\lr{ i \Hbar \frac{d}{dp’} }.
\end{aligned}
\end{equation}

Writing \( \Psi_\alpha(p’) = \braket{p’}{\alpha} \), the momentum space representation of Schrodinger’s equation for a position dependent potential is

\begin{equation}\label{eqn:shoMomentumSpace:220}
\boxed{
i \Hbar \PD{t}{} \Psi_\alpha(p’)
=
\lr{ \frac{(p’)^2}{2m} + V\lr{ i \Hbar \PDi{p’}{} } } \Psi_\alpha(p’).
}
\end{equation}

For the SHO Hamiltonian the potential is \( V(x) = (1/2) m \omega^2 x^2 \), so the Schrodinger equation is

\begin{equation}\label{eqn:shoMomentumSpace:240}
\begin{aligned}
i \Hbar \PD{t}{} \Psi_\alpha(p’)
&=
\lr{ \frac{(p’)^2}{2m} – \inv{2} m \omega^2 \Hbar^2
\frac{\partial^2}{\partial(p’)^2} } \Psi_\alpha(p’) \\
&=
\inv{2 m} \lr{ (p’)^2 – m^2 \omega^2 \Hbar^2 \frac{\partial^2}{\partial(p’)^2} } \Psi_\alpha(p’).
\end{aligned}
\end{equation}

To determine the wave functions, let’s non-dimensionalize this and compare to the position space Schrodinger equation. Let

\begin{equation}\label{eqn:shoMomentumSpace:260}
p_0^2 = m \omega \hbar,
\end{equation}

so
\begin{equation}\label{eqn:shoMomentumSpace:280}
\begin{aligned}
i \Hbar \PD{t}{} \Psi_\alpha(p’)
&=
\frac{p_0^2}{2 m} \lr{ \lr{\frac{p’}{p_0}}^2 –
\frac{\partial^2}{\partial(p’/p_0)^2} } \Psi_\alpha(p’) \\
&=
\frac{\omega \Hbar}{2}\lr{
– \frac{\partial^2}{\partial(p’/p_0)^2} +
\lr{\frac{p’}{p_0}}^2
} \Psi_\alpha(p’).
\end{aligned}
\end{equation}

Compare this to the position space equation with \( x_0^2 = m \omega/\Hbar \),

\begin{equation}\label{eqn:shoMomentumSpace:300}
\begin{aligned}
i \Hbar \PD{t}{} \Psi_\alpha(x’)
&=
\lr{ -\frac{\Hbar^2}{2m} \frac{\partial^2}{\partial(x’)^2}
+
\inv{2} m \omega^2 (x’)^2 }
\Psi_\alpha(x’) \\
&=
\frac{\Hbar^2}{2m}
\lr{ -\frac{\partial^2}{\partial(x’)^2}
+
\frac{m^2 \omega^2}{\Hbar^2} (x’)^2 }
\Psi_\alpha(x’) \\
&=
\frac{\Hbar^2 x_0^2}{2m}
\lr{
-\frac{\partial^2}{\partial(x’/x_0)^2}
+
\lr{\frac{x’}{x_0}}^2
}
\Psi_\alpha(x’) \\
&=
\frac{\Hbar \omega}{2}
\lr{
-\frac{\partial^2}{\partial(x’/x_0)^2}
+
\lr{\frac{x’}{x_0}}^2
}
\Psi_\alpha(x’).
\end{aligned}
\end{equation}

It’s clear that there is a straightforward duality relationship between the respective wave functions. Since

\begin{equation}\label{eqn:shoMomentumSpace:320}
\braket{x’}{n} =
\inv{\pi^{1/4} \sqrt{2^n n!} x_0^{n + 1/2}} \lr{ x’ – x_0^2 \frac{d}{dx’} }^n \exp\lr{ -\inv{2} \lr{\frac{x’}{x_0}}^2 },
\end{equation}

the momentum space wave functions are

\begin{equation}\label{eqn:shoMomentumSpace:340}
\braket{p’}{n} =
\inv{\pi^{1/4} \sqrt{2^n n!} p_0^{n + 1/2}} \lr{ p’ – p_0^2 \frac{d}{dp’} }^n \exp\lr{ -\inv{2} \lr{\frac{p’}{p_0}}^2 }.
\end{equation}

References

[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.