Paraview

A better 3D generalization of the Mandelbrot set.

February 9, 2021 math and physics play , , , , , , ,

I’ve been exploring 3D generalizations of the Mandelbrot set:

The iterative equation for the Mandelbrot set can be written in vector form ([1]) as:
\begin{equation}
\begin{aligned}
\Bz
&\rightarrow
\Bz \Be_1 \Bz + \Bc \\
&=
\Bz \lr{ \Be_1 \cdot \Bz }
+
\Bz \cdot \lr{ \Be_1 \wedge \Bz }
+ \Bc \\
&=
2 \Bz \lr{ \Be_1 \cdot \Bz }
–
\Bz^2\, \Be_1
+ \Bc
\end{aligned}
\end{equation}
Plotting this in 3D was an interesting challenge, but showed that the Mandelbrot set expressed above has rotational symmetry about the x-axis, which is kind of boring.

If all we require for a 3D fractal is to iterate a vector equation that is (presumably) at least quadratic, then we have lots of options. Here’s the first one that comes to mind:
\begin{equation}
\begin{aligned}
\Bz
&\rightarrow
\gpgradeone{ \Ba \Bz \Bb \Bz \Bc } + \Bd \\
&=
\lr{ \Ba \cdot \Bz } \lr{ \Bz \cross \lr{ \Bc \cross \Bz } }
+
\lr{ \Ba \cross \Bz } \lr{ \Bz \cdot \lr{ \Bc \cross \Bz } }
+ \Bd
.
\end{aligned}
\end{equation}
where we iterate starting, as usual with \( \Bz = 0 \) where \( \Bd \) is the point of interest to test for inclusion in the set. I tried this with
\begin{equation}\label{eqn:mandel3:n}
\begin{aligned}
\Ba &= (1,1,1) \\
\Bb &= (1,0,0) \\
\Bc &= (1,-1,0).
\end{aligned}
\end{equation}
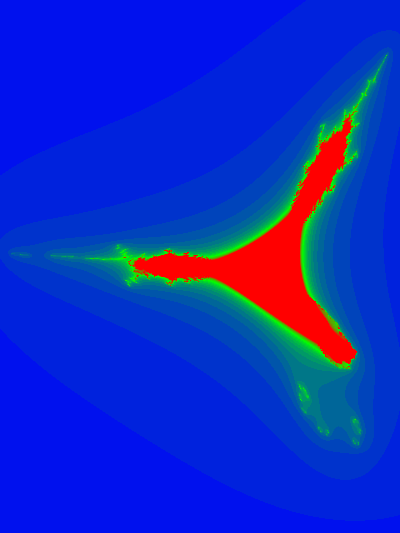
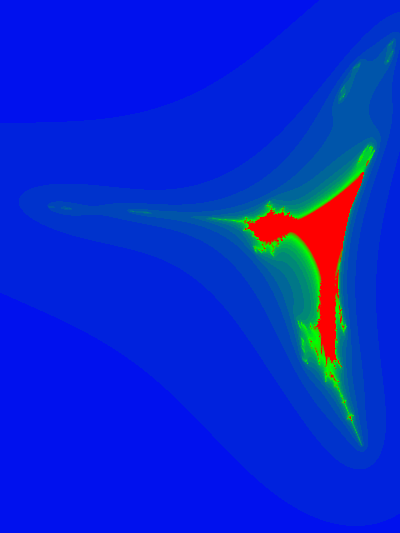
Here are some slice plots at various values of z

and an animation of the slices with respect to the z-axis:

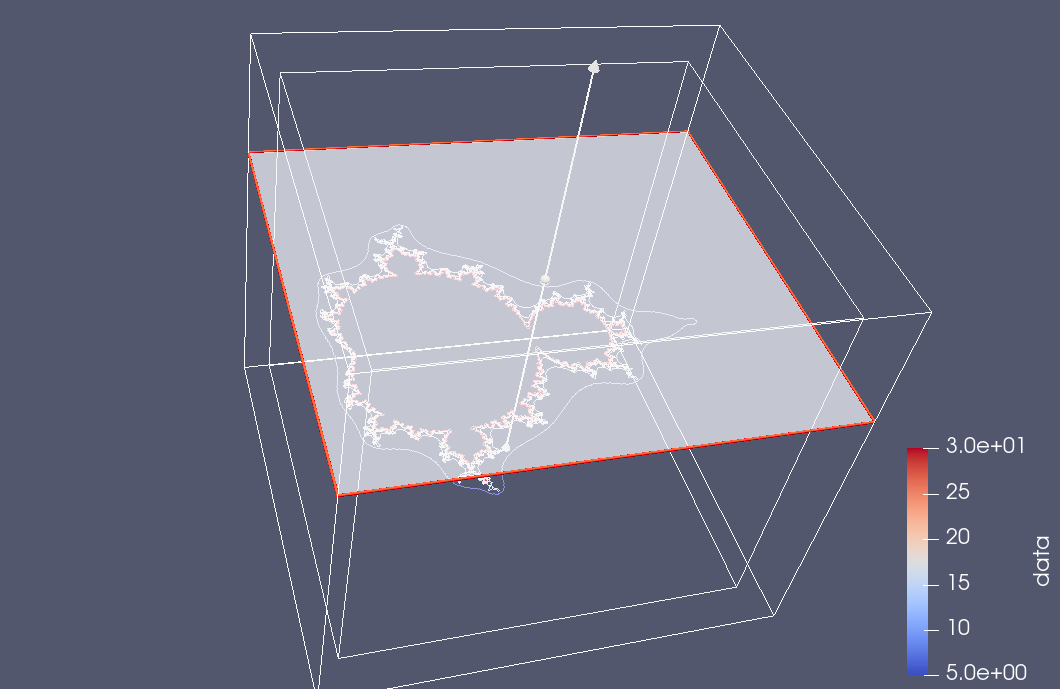
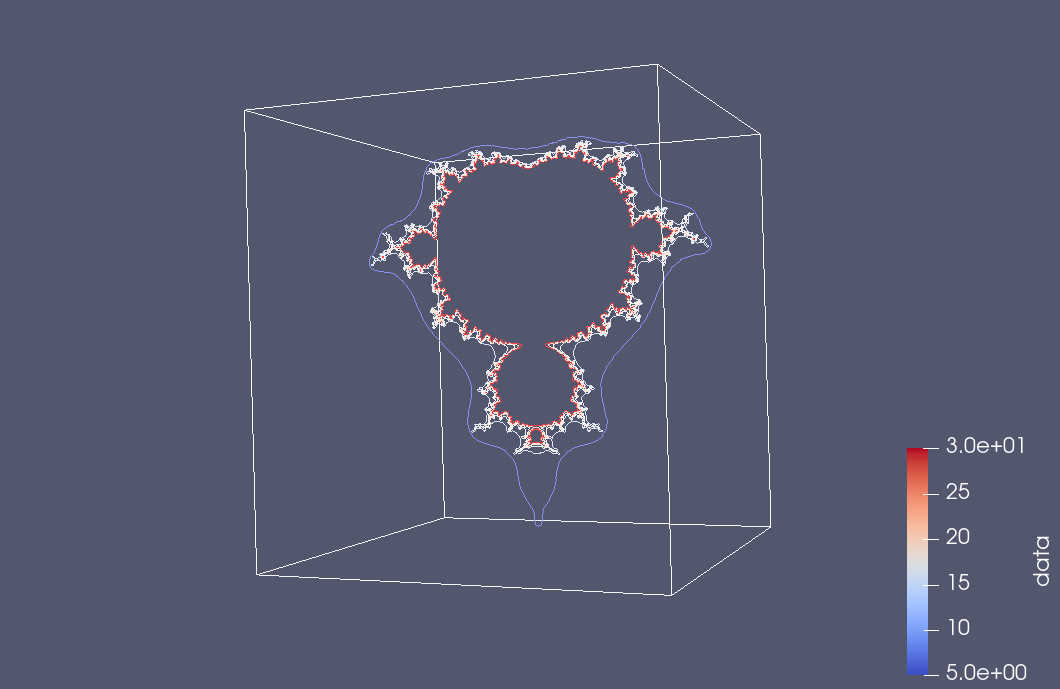
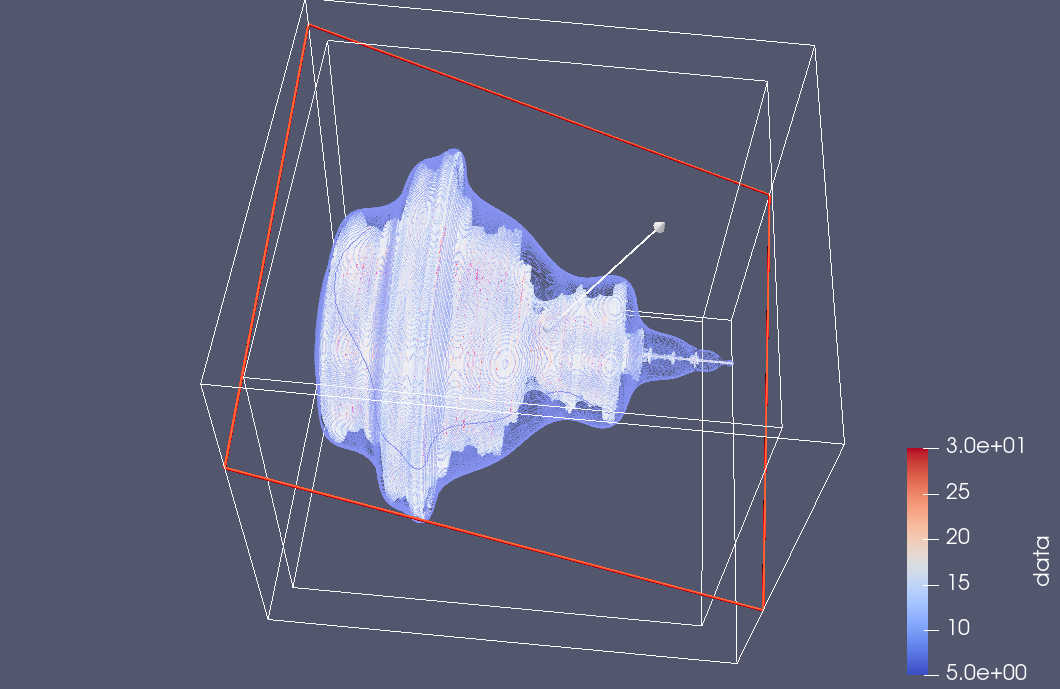
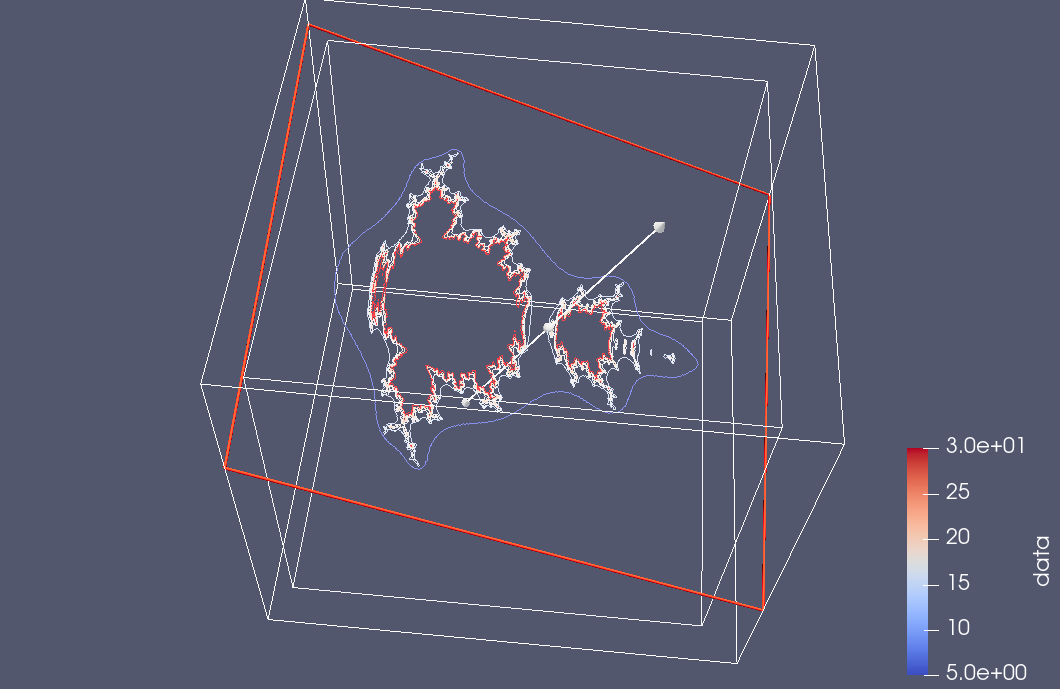
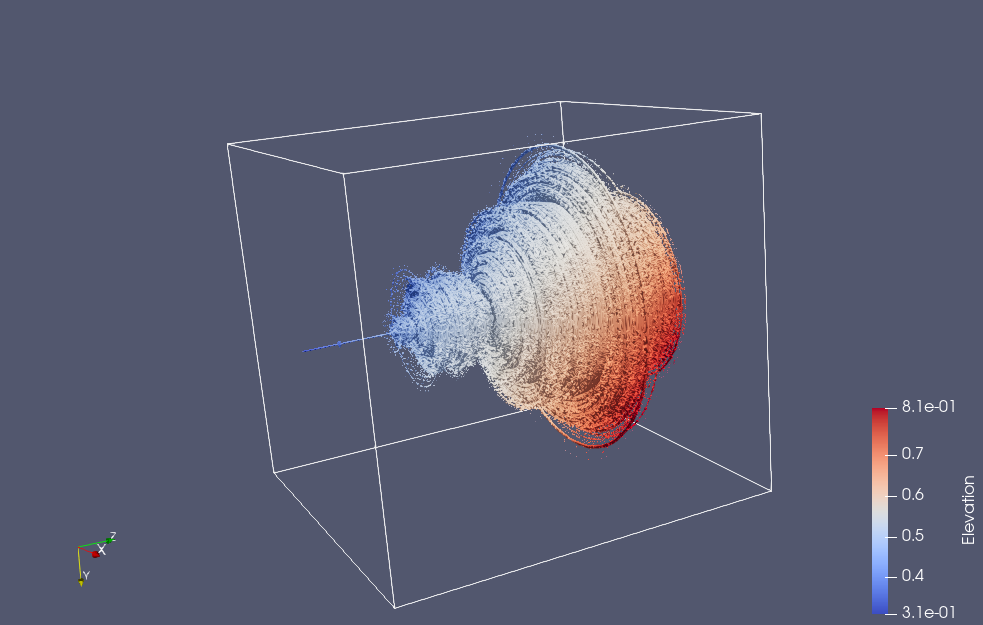
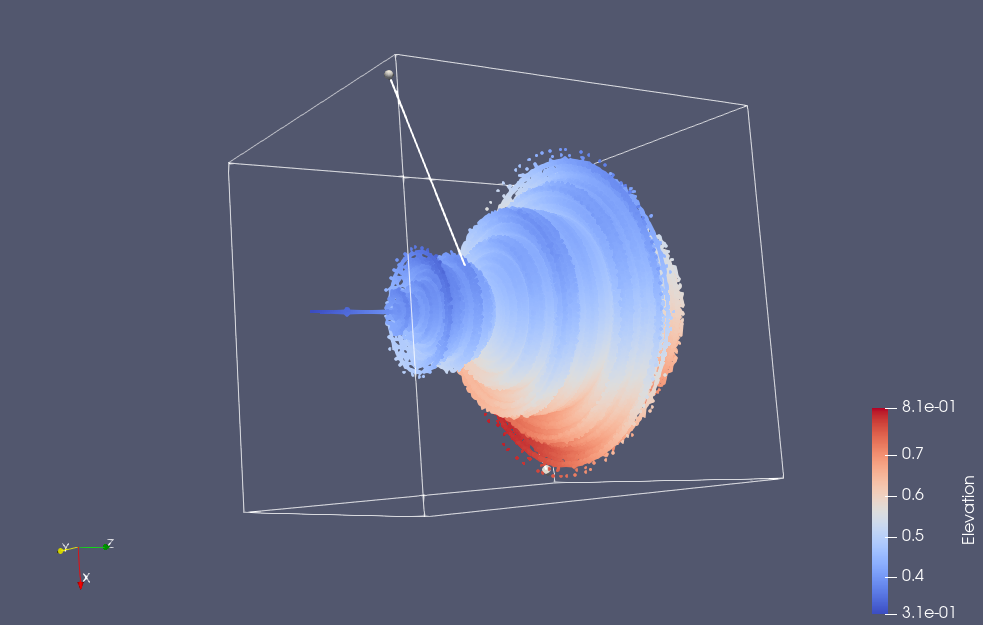
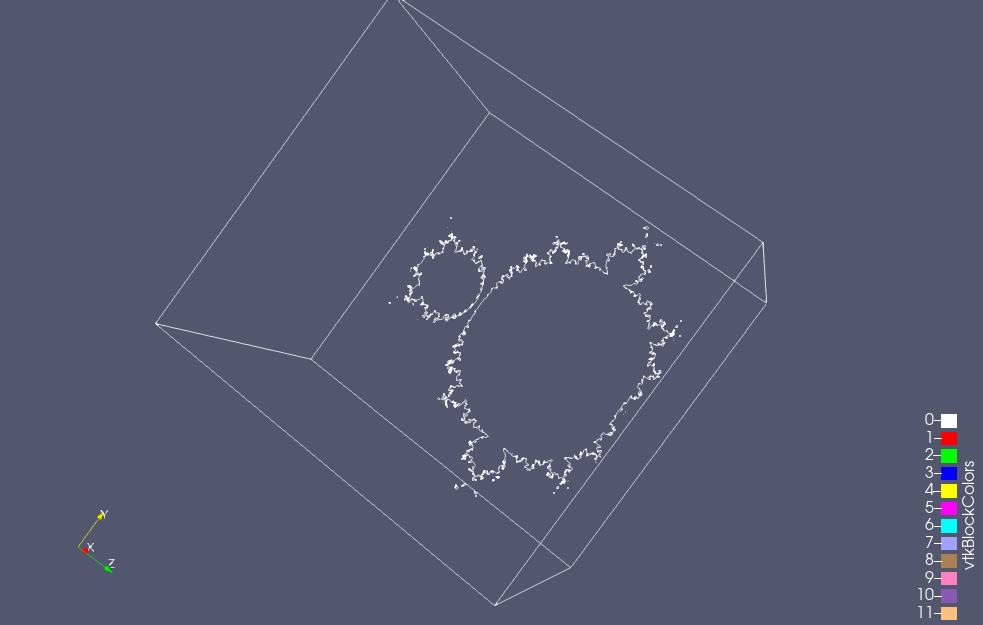
Here are a couple snapshots from a 3D Paraview rendering of a netCDF dataset of all the escape time values

Data collection and image creation used commit b042acf6ab7a5ba09865490b3f1fedaf0bd6e773 from my Mandelbrot generalization experimentation repository.

References

[1] L. Dorst, D. Fontijne, and S. Mann. Geometric Algebra for Computer Science. Morgan Kaufmann, San Francisco, 2007.

Slicing of the 3D Mandelbrot set, and analysis.

February 8, 2021 math and physics play , , , , , , ,

Some slices.

As followup to:

here is a bit more experimentation with Paraview slice filtering. This time I saved all the point data with the escape time counts, and rendered it with a few different contours

The default slice filter places the plane in the x-y orientation:

but we can also tilt it in the Paraview render UI

and suppress the contour view to see just the slice

As a very GUI challenged user, I don’t find the interface particularly intuitive, but have at least figured out this one particular slicing task, which is kind of cool.  It’s impressive that the UI can drive interesting computational tasks without having to regenerate or reload any of the raw data itself.  This time I was using the MacOSX Paraview client, which is nicer looking than the Windows version, but has some weird glitches in the file dialogues.

Analysis.

The graphing play above shows some apparent rotational symmetry our vector equivalent to the Mandelbrot equation
\begin{equation}
\Bx \rightarrow \Bx \Be_1 \Bx + \Bc.
\end{equation}
It was not clear to me if this symmetry existed, as there were artifacts in the plots that made it appear that there was irregularity. However, some thought shows that this irregularity is strictly due to sampling error, and perhaps also due to limitations in the plotting software, as such an uneven surface is probably tricky to deal with.

To see this, here are the first few iterations of the Mandlebrot sequence for an arbitary starting vector \( \Bc \).
\begin{equation}
\begin{aligned}
\Bx_0 &= \Bc \\
\Bx_1 &= \Bc \Be_1 \Bc + \Bc \\
\Bx_2 &= \lr{ \Bc \Be_1 \Bc + \Bc } \Be_1 \lr{ \Bc \Be_1 \Bc + \Bc } + \Bc \Be_1 \Bc + \Bc.
\end{aligned}
\end{equation}

Now, what happens when we rotate the starting vector \( \Bc \) in the \( y-z \) plane. The rotor for such a rotation is
\begin{equation}
R = \exp\lr{ e_{23} \theta/2 },
\end{equation}
where
\begin{equation}
\Bc \rightarrow R \Bc \tilde{R}.
\end{equation}
Observe that if \( \Bc \) is parallel to the x-axis, then this rotation leaves the starting point invariant, as \( \Be_1 \) commutes with \( R \). That is
\begin{equation}
R \Be_1 \tilde{R} =
\Be_1 R \tilde{R} = \Be_1.
\end{equation}
Let \( \Bc’ = R \Bc \tilde{R} \), so that
\begin{equation}
\Bx_0′ = R \Bc \tilde{R} = R \Bx_0 \tilde{R} .
\end{equation}
\begin{equation}
\begin{aligned}
\Bx_1′
&= R \Bc \tilde{R} \Be_1 R \Bc \tilde{R} + R \Bc \tilde{R} \\
&= R \Bc \Be_1 \Bc \tilde{R} + R \Bc \tilde{R} \\
&= R \lr{ \Bc \Be_1 \Bc R + \Bc } \tilde{R} \\
&= R \Bx_1 \tilde{R}.
\end{aligned}
\end{equation}
\begin{equation}\label{eqn:m2:n}
\begin{aligned}
\Bx_2′
&= \Bx_1′ \Be_1 \Bx_1′ + \Bc’ \\
&= R \Bx_1 \tilde{R} \Be_1 R \Bx_1 \tilde{R} + R \Bc \tilde{R} \\
&= R \Bx_1 \Be_1 \Bx_1 \tilde{R} + R \Bc \tilde{R} \\
&= R \lr{ \Bx_1 \Be_1 \Bx_1 + \Bc } \tilde{R} \\
&= R \Bx_2 \tilde{R}.
\end{aligned}
\end{equation}

The pattern is clear. If we rotate the starting point in the y-z plane, iterating the Mandelbrot sequence results in precisely the same rotation of the x-y plane Mandelbrot sequence. So the apparent rotational symmetry in the 3D iteration of the Mandelbrot vector equation is exactly that. This is an unfortunately boring 3D fractal. All of the interesting fractal nature occurs in the 2D plane, and the rest is just a consequence of rotating that image around the x-axis. We get some interesting fractal artifacts if we slice the rotated Mandelbrot image.

Some 3D renderings of the Mandelbrot set.

February 7, 2021 math and physics play , , , , ,

As mentioned previously, using geometric algebra we can convert the iterative equation for the Mandelbrot set from complex number form
\begin{equation}
z \rightarrow z^2 + c,
\end{equation}
to an equivalent vector form
\begin{equation}
\mathbf{x} \rightarrow \mathbf{x} \mathbf{e} \mathbf{x} + \mathbf{c},
\end{equation}
where \( \mathbf{e} \) represents the x-axis (say). Geometrically, each iteration takes \( \mathbf{e} \) and reflects it about the direction of \( \mathbf{x} \), then scales that by \( \mathbf{x}^2 \) and adds \( \mathbf{c} \).

To get the usual 2D Mandelbrot set, one iterates with vectors that lie only in the x-y plane, but we can treat the Mandelbrot set as a 3D solid if we remove the x-y plane restriction.

Last time I animated slices of the 3D set, but after a whole lot of messing around I managed to save the data for all the interior points of the 3D set in netCDF format, and render the solid using Paraview. Paraview has tons of filters available, and experimenting with them is pretty time consuming, but here are some initial screenshots of the 3D Mandelbrot set:

It’s interesting that much of the characteristic detail of the Mandelbrot set is not visible in the 3D volume, but if we slice that volume, you can then you can see it again.  Here’s a slice taken close to the z=0 plane (but far enough that the “CN tower” portion of the set is not visible)

You can also see some of that detail if the opacity of the rendering is turned way down:

If you look carefully at the images above, you’ll see that the axis labels are wrong.  I think that I’ve screwed up one of the stride related parameters to my putVar call, and I end up with x+z transposed in the axes labels when visualized.