quasi-convex

ECE1505H Convex Optimization. Lecture 6: First and second order conditions. Taught by Prof.\ Stark Draper

February 1, 2017 ece1505 , , , , , , , ,

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

These are notes for the UofT course ECE1505H, Convex Optimization, taught by Prof. Stark Draper, from [1].

Today

  • First and second order conditions for convexity of differentiable functions.
  • Consequences of convexity: local and global optimality.
  • Properties.

Quasi-convex

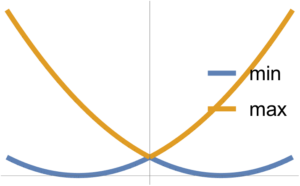
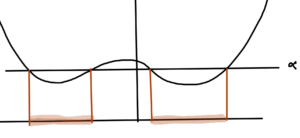
\( F_1 \) and \( F_2 \) convex implies \( \max( F_1, F_2) \) convex.

 

fig. 1. Min and Max

Note that \( \min(F_1, F_2) \) is NOT convex.

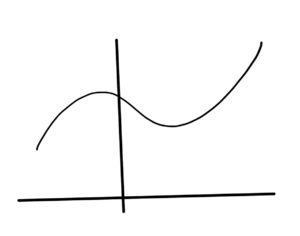
If \( F : \mathbb{R}^n \rightarrow \mathbb{R} \) is convex, then \( F( \Bx_0 + t \Bv ) \) is convex in \( t\,\forall t \in \mathbb{R}, \Bx_0 \in \mathbb{R}^n, \Bv \in \mathbb{R}^n \), provided \( \Bx_0 + t \Bv \in \textrm{dom} F \).

Idea: Restrict to a line (line segment) in \( \textrm{dom} F \). Take a cross section or slice through \( F \) alone the line. If the result is a 1D convex function for all slices, then \( F \) is convex.

This is nice since it allows for checking for convexity, and is also nice numerically. Attempting to test a given data set for non-convexity with some random lines can help disprove convexity. However, to show that \( F \) is convex it is required to test all possible slices (which isn’t possible numerically, but is in some circumstances possible analytically).

Differentiable (convex) functions

Definition: First order condition.

If

\begin{equation*}
F : \mathbb{R}^n \rightarrow \mathbb{R}
\end{equation*}

is differentiable, then \( F \) is convex iff \( \textrm{dom} F \) is a convex set and \( \forall \Bx, \Bx_0 \in \textrm{dom} F \)

\begin{equation*}
F(\Bx) \ge F(\Bx_0) + \lr{\spacegrad F(\Bx_0)}^\T (\Bx – \Bx_0).
\end{equation*}

This is the first order Taylor expansion. If \( n = 1 \), this is \( F(x) \ge F(x_0) + F'(x_0) ( x – x_0) \).

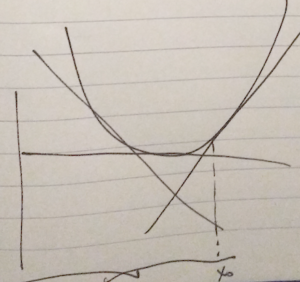
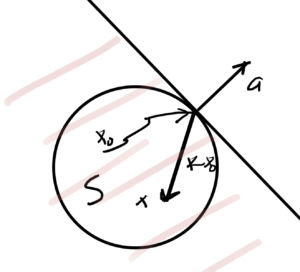
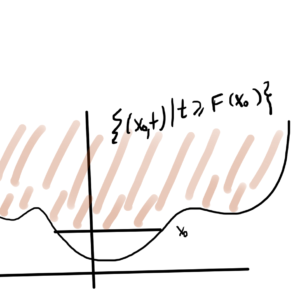
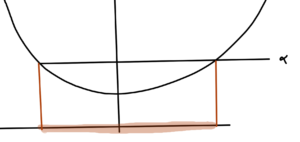
The first order condition says a convex function \underline{always} lies above its first order approximation, as sketched in fig. 3.

 

fig. 2. First order approximation lies below convex function

When differentiable, the supporting plane is the tangent plane.

Definition: Second order condition

If \( F : \mathbb{R}^n \rightarrow \mathbb{R} \) is twice differentiable, then \( F \) is convex iff \( \textrm{dom} F \) is a convex set and \( \spacegrad^2 F(\Bx) \ge 0 \,\forall \Bx \in \textrm{dom} F\).

The Hessian is always symmetric, but is not necessarily positive. Recall that the Hessian is the matrix of the second order partials \( (\spacegrad F)_{ij} = \partial^2 F/(\partial x_i \partial x_j) \).

The scalar case is \( F”(x) \ge 0 \, \forall x \in \textrm{dom} F \).

An implication is that if \( F \) is convex, then \( F(x) \ge F(x_0) + F'(x_0) (x – x_0) \,\forall x, x_0 \in \textrm{dom} F\)

Since \( F \) is convex, \( \textrm{dom} F \) is convex.

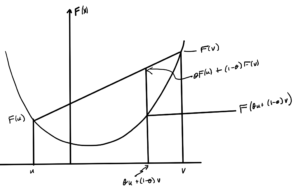
Consider any 2 points \( x, y \in \textrm{dom} F \), and \( \theta \in [0,1] \). Define

\begin{equation}\label{eqn:convexOptimizationLecture6:60}
z = (1-\theta) x + \theta y \in \textrm{dom} F,
\end{equation}

then since \( \textrm{dom} F \) is convex

\begin{equation}\label{eqn:convexOptimizationLecture6:80}
F(z) =
F( (1-\theta) x + \theta y )
\le
(1-\theta) F(x) + \theta F(y )
\end{equation}

Reordering

\begin{equation}\label{eqn:convexOptimizationLecture6:220}
\theta F(x) \ge
\theta F(x) + F(z) – F(x),
\end{equation}

or
\begin{equation}\label{eqn:convexOptimizationLecture6:100}
F(y) \ge
F(x) + \frac{F(x + \theta(y-x)) – F(x)}{\theta},
\end{equation}

which is, in the limit,

\begin{equation}\label{eqn:convexOptimizationLecture6:120}
F(y) \ge
F(x) + F'(x) (y – x),
\end{equation}

completing one direction of the proof.

To prove the other direction, showing that

\begin{equation}\label{eqn:convexOptimizationLecture6:140}
F(x) \ge F(x_0) + F'(x_0) (x – x_0),
\end{equation}

implies that \( F \) is convex. Take any \( x, y \in \textrm{dom} F \) and any \( \theta \in [0,1] \). Define

\begin{equation}\label{eqn:convexOptimizationLecture6:160}
z = \theta x + (1 -\theta) y,
\end{equation}

which is in \( \textrm{dom} F \) by assumption. We want to show that

\begin{equation}\label{eqn:convexOptimizationLecture6:180}
F(z) \le \theta F(x) + (1-\theta) F(y).
\end{equation}

By assumption

  1. \( F(x) \ge F(z) + F'(z) (x – z) \)
  2. \( F(y) \ge F(z) + F'(z) (y – z) \)

Compute

\begin{equation}\label{eqn:convexOptimizationLecture6:200}
\begin{aligned}
\theta F(x) + (1-\theta) F(y)
&\ge
\theta \lr{ F(z) + F'(z) (x – z) }
+ (1-\theta) \lr{ F(z) + F'(z) (y – z) } \\
&=
F(z) + F'(z) \lr{ \theta( x – z) + (1-\theta) (y-z) } \\
&=
F(z) + F'(z) \lr{ \theta x + (1-\theta) y – \theta z – (1 -\theta) z } \\
&=
F(z) + F'(z) \lr{ \theta x + (1-\theta) y – z} \\
&=
F(z) + F'(z) \lr{ z – z} \\
&= F(z).
\end{aligned}
\end{equation}

Proof of the 2nd order case for \( n = 1 \)

Want to prove that if

\begin{equation}\label{eqn:convexOptimizationLecture6:240}
F : \mathbb{R} \rightarrow \mathbb{R}
\end{equation}

is a convex function, then \( F”(x) \ge 0 \,\forall x \in \textrm{dom} F \).

By the first order conditions \( \forall x \ne y \in \textrm{dom} F \)

\begin{equation}\label{eqn:convexOptimizationLecture6:260}
\begin{aligned}
F(y) &\ge F(x) + F'(x) (y – x)
F(x) &\ge F(y) + F'(y) (x – y)
\end{aligned}
\end{equation}

Can combine and get

\begin{equation}\label{eqn:convexOptimizationLecture6:280}
F'(x) (y-x) \le F(y) – F(x) \le F'(y)(y-x)
\end{equation}

Subtract the two derivative terms for

\begin{equation}\label{eqn:convexOptimizationLecture6:340}
\frac{(F'(y) – F'(x))(y – x)}{(y – x)^2} \ge 0,
\end{equation}

or
\begin{equation}\label{eqn:convexOptimizationLecture6:300}
\frac{F'(y) – F'(x)}{y – x} \ge 0.
\end{equation}

In the limit as \( y \rightarrow x \), this is
\begin{equation}\label{eqn:convexOptimizationLecture6:320}
\boxed{
F”(x) \ge 0 \,\forall x \in \textrm{dom} F.
}
\end{equation}

Now prove the reverse condition:

If \( F”(x) \ge 0 \,\forall x \in \textrm{dom} F \subseteq \mathbb{R} \), implies that \( F : \mathbb{R} \rightarrow \mathbb{R} \) is convex.

Note that if \( F”(x) \ge 0 \), then \( F'(x) \) is non-decreasing in \( x \).

i.e. If \( x < y \), where \( x, y \in \textrm{dom} F\), then

\begin{equation}\label{eqn:convexOptimizationLecture6:360}
F'(x) \le F'(y).
\end{equation}

Consider any \( x,y \in \textrm{dom} F\) such that \( x < y \), where

\begin{equation}\label{eqn:convexOptimizationLecture6:380}
F(y) – F(x) = \int_x^y F'(t) dt \ge F'(x) \int_x^y 1 dt = F'(x) (y-x).
\end{equation}

This tells us that

\begin{equation}\label{eqn:convexOptimizationLecture6:400}
F(y) \ge F(x) + F'(x)(y – x),
\end{equation}

which is the first order condition. Similarly consider any \( x,y \in \textrm{dom} F\) such that \( x < y \), where

\begin{equation}\label{eqn:convexOptimizationLecture6:420}
F(y) – F(x) = \int_x^y F'(t) dt \le F'(y) \int_x^y 1 dt = F'(y) (y-x).
\end{equation}

This tells us that

\begin{equation}\label{eqn:convexOptimizationLecture6:440}
F(x) \ge F(y) + F'(y)(x – y).
\end{equation}

Vector proof:

\( F \) is convex iff \( F(\Bx + t \Bv) \) is convex \( \forall \Bx,\Bv \in \mathbb{R}^n, t \in \mathbb{R} \), keeping \( \Bx + t \Bv \in \textrm{dom} F\).

Let
\begin{equation}\label{eqn:convexOptimizationLecture6:460}
h(t ; \Bx, \Bv) = F(\Bx + t \Bv)
\end{equation}

then \( h(t) \) satisfies scalar first and second order conditions for all \( \Bx, \Bv \).

\begin{equation}\label{eqn:convexOptimizationLecture6:480}
h(t) = F(\Bx + t \Bv) = F(g(t)),
\end{equation}

where \( g(t) = \Bx + t \Bv \), where

\begin{equation}\label{eqn:convexOptimizationLecture6:500}
\begin{aligned}
F &: \mathbb{R}^n \rightarrow \mathbb{R} \\
g &: \mathbb{R} \rightarrow \mathbb{R}^n.
\end{aligned}
\end{equation}

This is expressing \( h(t) \) as a composition of two functions. By the first order condition for scalar functions we know that

\begin{equation}\label{eqn:convexOptimizationLecture6:520}
h(t) \ge h(0) + h'(0) t.
\end{equation}

Note that

\begin{equation}\label{eqn:convexOptimizationLecture6:540}
h(0) = \evalbar{F(\Bx + t \Bv)}{t = 0} = F(\Bx).
\end{equation}

Let’s figure out what \( h'(0) \) is. Recall hat for any \( \tilde{F} : \mathbb{R}^n \rightarrow \mathbb{R}^m \)

\begin{equation}\label{eqn:convexOptimizationLecture6:560}
D \tilde{F} \in \mathbb{R}^{m \times n},
\end{equation}

and
\begin{equation}\label{eqn:convexOptimizationLecture6:580}
{D \tilde{F}(\Bx)}_{ij} = \PD{x_j}{\tilde{F_i}(\Bx)}
\end{equation}

This is one function per row, for \( i \in [1,m], j \in [1,n] \). This gives

\begin{equation}\label{eqn:convexOptimizationLecture6:600}
\begin{aligned}
\frac{d}{dt} F(\Bx + \Bv t)
&=
\frac{d}{dt} F( g(t) ) \\
&=
\frac{d}{dt} h(t) \\
&= D h(t) \\
&= D F(g(t)) \cdot D g(t)
\end{aligned}
\end{equation}

The first matrix is in \( \mathbb{R}^{1\times n} \) whereas the second is in \( \mathbb{R}^{n\times 1} \), since \( F : \mathbb{R}^n \rightarrow \mathbb{R} \) and \( g : \mathbb{R} \rightarrow \mathbb{R}^n \). This gives

\begin{equation}\label{eqn:convexOptimizationLecture6:620}
\frac{d}{dt} F(\Bx + \Bv t)
= \evalbar{D F(\tilde{\Bx})}{\tilde{\Bx} = g(t)} \cdot D g(t).
\end{equation}

That first matrix is

\begin{equation}\label{eqn:convexOptimizationLecture6:640}
\begin{aligned}
\evalbar{D F(\tilde{\Bx})}{\tilde{\Bx} = g(t)}
&=
\evalbar{
\lr{\begin{bmatrix}
\PD{\tilde{x}_1}{ F(\tilde{\Bx})} &
\PD{\tilde{x}_2}{ F(\tilde{\Bx})} & \cdots
\PD{\tilde{x}_n}{ F(\tilde{\Bx})}
\end{bmatrix}
}}{ \tilde{\Bx} = g(t) = \Bx + t \Bv } \\
&=
\evalbar{
\lr{ \spacegrad F(\tilde{\Bx}) }^\T
}{
\tilde{\Bx} = g(t)
} \\
=
\lr{ \spacegrad F(g(t)) }^\T.
\end{aligned}
\end{equation}

The second Jacobian is

\begin{equation}\label{eqn:convexOptimizationLecture6:660}
D g(t)
=
D
\begin{bmatrix}
g_1(t) \\
g_2(t) \\
\vdots \\
g_n(t) \\
\end{bmatrix}
=
D
\begin{bmatrix}
x_1 + t v_1 \\
x_2 + t v_2 \\
\vdots \\
x_n + t v_n \\
\end{bmatrix}
=
\begin{bmatrix}
v_1 \\
v_1 \\
\vdots \\
v_n \\
\end{bmatrix}
=
\Bv.
\end{equation}

so

\begin{equation}\label{eqn:convexOptimizationLecture6:680}
h'(t) = D h(t) = \lr{ \spacegrad F(g(t))}^\T \Bv,
\end{equation}

and
\begin{equation}\label{eqn:convexOptimizationLecture6:700}
h'(0) = \lr{ \spacegrad F(g(0))}^\T \Bv
=
\lr{ \spacegrad F(\Bx)}^\T \Bv.
\end{equation}

Finally

\begin{equation}\label{eqn:convexOptimizationLecture6:720}
\begin{aligned}
F(\Bx + t \Bv)
&\ge h(0) + h'(0) t \\
&= F(\Bx) + \lr{ \spacegrad F(\Bx) }^\T (t \Bv) \\
&= F(\Bx) + \innerprod{ \spacegrad F(\Bx) }{ t \Bv}.
\end{aligned}
\end{equation}

Which is true for all \( \Bx, \Bx + t \Bv \in \textrm{dom} F \). Note that the quantity \( t \Bv \) is a shift.

Epigraph

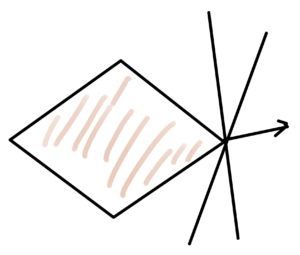
Recall that if \( (\Bx, t) \in \textrm{epi} F \) then \( t \ge F(\Bx) \).

\begin{equation}\label{eqn:convexOptimizationLecture6:740}
t \ge F(\Bx) \ge F(\Bx_0) + \lr{\spacegrad F(\Bx_0) }^\T (\Bx – \Bx_0),
\end{equation}

or

\begin{equation}\label{eqn:convexOptimizationLecture6:760}
0 \ge
-(t – F(\Bx_0)) + \lr{\spacegrad F(\Bx_0) }^\T (\Bx – \Bx_0),
\end{equation}

In block matrix form

\begin{equation}\label{eqn:convexOptimizationLecture6:780}
0 \ge
\begin{bmatrix}
\lr{ \spacegrad F(\Bx_0) }^\T & -1
\end{bmatrix}
\begin{bmatrix}
\Bx – \Bx_0 \\
t – F(\Bx_0)
\end{bmatrix}
\end{equation}

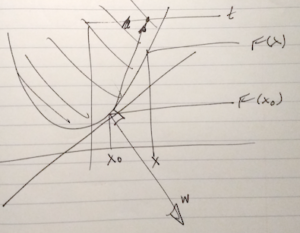
With \( \Bw =
\begin{bmatrix}
\lr{ \spacegrad F(\Bx_0) }^\T & -1
\end{bmatrix} \), the geometry of the epigraph relation to the half plane is sketched in fig. 3.

 

fig. 3. Half planes and epigraph.

References

[1] Stephen Boyd and Lieven Vandenberghe. Convex optimization. Cambridge university press, 2004.

ECE1505H Convex Optimization. Lecture 5: Sets, epigraphs, quasi-convexity, and sublevel sets. Taught by Prof. Stark Draper

January 26, 2017 ece1505 , , , , , , , ,

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

These are notes for the UofT course ECE1505H, Convex Optimization, taught by Prof. Stark Draper, from [1].

Last time

  • examples of sets: planes, half spaces, balls, ellipses, cone of positive semi-definite matrices
  • generalized inequalities
  • examples of convexity preserving operations

Today

  • more examples of convexity preserving operations
  • separating and supporting hyperplanes
  • basic definitions of convex functions
  • epigraphs, quasi-convexity, sublevel sets
  • first and second order conditions for convexity of differentiable functions.

Operations that preserve convexity

If \( S_\alpha \) is convex \( \forall \alpha \in A \), then

\begin{equation}\label{eqn:convexOptimizationLecture5:40}
\cup_{\alpha \in A} S_\alpha,
\end{equation}

is convex.

Example:

\begin{equation}\label{eqn:convexOptimizationLecture5:60}
F(\Bx) = A \Bx + \Bb
\end{equation}

\begin{equation}\label{eqn:convexOptimizationLecture5:80}
\begin{aligned}
\Bx &\in \mathbb{R}^n \\
A &\in \mathbb{R}^{m \times n} \\
F &: \mathbb{R}^{n} \rightarrow \mathbb{R}^m \\
\Bb &\in \mathbb{R}^m
\end{aligned}
\end{equation}

  1. If \( S \in \mathbb{R}^n \) is convex, then\begin{equation}\label{eqn:convexOptimizationLecture5:100}
    F(S) = \setlr{ F(\Bx) | \Bx \in S }
    \end{equation}is convex if \( F \) is affine.
  2. If \( S \in \mathbb{R}^m \) is convex, then\begin{equation}\label{eqn:convexOptimizationLecture5:120}
    F^{-1}(S) = \setlr{ \Bx | F(\Bx) \in S }
    \end{equation}

    is convex.

Example:

\begin{equation}\label{eqn:convexOptimizationLecture5:140}
\setlr{ \By | \By = A \Bx + \Bb, \Norm{\Bx} \le 1}
\end{equation}

is convex. Here \( A \Bx + \Bb \) is an affine function (\(F(\Bx)\). This is the image of a (convex) unit ball, through an affine map.

Earlier saw when defining ellipses

\begin{equation}\label{eqn:convexOptimizationLecture5:160}
\By = P^{1/2} \Bx + \Bx_c
\end{equation}

Example :

\begin{equation}\label{eqn:convexOptimizationLecture5:180}
\setlr{ \Bx | \Norm{ A \Bx + \Bb } \le 1 },
\end{equation}

is convex. This can be seen by writing

\begin{equation}\label{eqn:convexOptimizationLecture5:200}
\begin{aligned}
\setlr{ \Bx | \Norm{ A \Bx + \Bb } \le 1 }
&=
\setlr{ \Bx | \Norm{ F(\Bx) } \le 1 } \\
&=
\setlr{ \Bx | F(\Bx) \in \mathcal{B} },
\end{aligned}
\end{equation}

where \( \mathcal{B} = \setlr{ \By | \Norm{\By} \le 1 } \). This is the pre-image (under \(F()\)) of a unit norm ball.

Example:

\begin{equation}\label{eqn:convexOptimizationLecture5:220}
\setlr{ \Bx \in \mathbb{R}^n | x_1 A_1 + x_2 A_2 + \cdots x_n A_n \le \mathcal{B} }
\end{equation}

where \( A_i \in S^m \) and \( \mathcal{B} \in S^m \), and the inequality is a matrix inequality. This is a convex set. The constraint is a “linear matrix inequality” (LMI).

This has to do with an affine map:

\begin{equation}\label{eqn:convexOptimizationLecture5:240}
F(\Bx) = B – 1 x_1 A_1 – x_2 A_2 – \cdots x_n A_n \ge 0
\end{equation}

(positive semi-definite inequality). This is a mapping

\begin{equation}\label{eqn:convexOptimizationLecture5:480}
F : \mathbb{R}^n \rightarrow S^m,
\end{equation}

since all \( A_i \) and \( B \) are in \( S^m \).

This \( F(\Bx) = B – A(\Bx) \) is a constant and a factor linear in x, so is affine. Can be written

\begin{equation}\label{eqn:convexOptimizationLecture5:260}
\setlr{ \Bx | B – A(\Bx) \ge 0 }
=
\setlr{ \Bx | B – A(\Bx) \in S^m_{+} }
\end{equation}

This is a pre-image of a cone of PSD matrices, which is convex. Therefore, this is a convex set.

Separating hyperplanes

Theorem: Separating hyperplanes

If \( S, T \subseteq \mathbb{R}^n \) are convex and disjoint
i.e. \( S \cup T = 0\), then
there exists on \( \Ba \in \mathbb{R}^n \) \( \Ba \ne 0 \) and a \( \Bb \in \mathbb{R}^n \) such that

\begin{equation*}
\Ba^\T \Bx \ge \Bb \, \forall \Bx \in S
\end{equation*}

and
\begin{equation*}
\Ba^\T \Bx < \Bb \,\forall \Bx \in T.
\end{equation*}

An example of a hyperplanes that separates two sets and two sets that are not separable is sketched in fig 1.1

Proof in the book.

Theorem: Supporting hyperplane
If \( S \) is convex then \( \forall x_0 \in \partial S = \textrm{cl}(S) \ \textrm{int}(S) \), where
\( \partial S \) is the boundary of \( S \), then \( \exists \) an \( \Ba \ne 0 \in \mathbb{R}^n \) such that \( \Ba^\T \Bx \le \Ba^\T x_0 \, \forall \Bx \in S \).

Here \( \ \) denotes “without”.

An example is sketched in fig. 3, for which

fig. 3. Supporting hyperplane.

  • The vector \( \Ba \) perpendicular to tangent plane.
  • inner product \( \Ba^\T (\Bx – \Bx_0) \le 0 \).

A set with a supporting hyperplane is sketched in fig 4a whereas fig 4b shows that there is not necessarily a unique supporting hyperplane at any given point, even if \( S \) is convex.

 

fig 4a. Set with supporting hyperplane.

 

fig 4b. No unique supporting hyperplane possible.

basic definitions of convex functions

Theorem: Convex functions
If \( F : \mathbb{R}^n \rightarrow \mathbb{R} \) is defined on a convex domain (i.e. \( \textrm{dom} F \subseteq \mathbb{R}^n \) is a convex set), then \( F \) is convex if \( \forall \Bx, \By \in \textrm{dom} F \), \( \forall \theta \in [0,1] \in \mathbb{R} \)

\begin{equation}\label{eqn:convexOptimizationLecture5:340}
F( \theta \Bx + (1-\theta) \By \le \theta F(\Bx) + (1-\theta) F(\By)
\end{equation}

An example is sketched in fig. 5.

 

fig. 5. Example of convex function.

Remarks

  • Require \( \textrm{dom} F \) to be a convex set. This is required so that the function at the point \( \theta u + (1-\theta) v \) can be evaluated. i.e. so that \( F(\theta u + (1-\theta) v) \) is well defined. Example: \( \textrm{dom} F = (-\infty, 0] \cup [1, \infty) \) is not okay, because a linear combination in \( (0,1) \) would be undesirable.
  • Parameter \( \theta \) is “how much up” the line segment connecting \( (u, F(u) \) and \( (v, F(v) \). This line segment never below the bottom of the bowl.
    The function is \underlineAndIndex{concave}, if \( -F \) is convex.
    i.e. If the convex function is flipped upside down. That is\begin{equation}\label{eqn:convexOptimizationLecture5:360}
    F(\theta \Bx + (1-\theta) \By ) \ge \theta F(\Bx) + (1-\theta) F(\By) \,\forall \Bx,\By \in \textrm{dom} F, \theta \in [0,1].
    \end{equation}
  • a “strictly” convex function means \(\forall \theta \in [0,1] \)\begin{equation}\label{eqn:convexOptimizationLecture5:380}
    F(\theta \Bx + (1-\theta) \By ) < \theta F(\Bx) + (1-theta) F(\By).
    \end{equation}
  • Strictly concave function \( F \) means \( -F \) is strictly convex.
  • Examples:\imageFigure{../figures/ece1505-convex-optimization/l5Fig6a}{}{fig:l5:l5Fig6a}{0.2}

    fig 6a. Not convex or concave.

     

    fig 6b. Not strictly convex

Definition: Epigraph of a function

The epigraph \( \textrm{epi} F \) of a function \( F : \mathbb{R}^n \rightarrow \mathbb{R} \) is

\begin{equation*}
\textrm{epi} F = \setlr{ (\Bx,t) \in \mathbb{R}^{n +1} | \Bx \in \textrm{dom} F, t \ge F(\Bx) },
\end{equation*}

where \( \Bx \in \mathbb{R}^n, t \in \mathbb{R} \).

 

fig. 7. Epigraph.

Theorem: Convexity and epigraph.
If \( F \) is convex implies \( \textrm{epi} F \) is a convex set.

Proof:

For convex function, a line segment connecting any 2 points on function is above the function. i.e. it is \( \textrm{epi} F \).

Many authors will go the other way around, showing \ref{dfn:convexOptimizationLecture5:400} from \ref{thm:convexOptimizationLecture5:420}. That is:

Pick any 2 points in \( \textrm{epi} F \), \( (\Bx,\mu) \in \textrm{epi} F\) and \( (\By, \nu) \in \textrm{epi} F \). Consider convex combination

\begin{equation}\label{eqn:convexOptimizationLecture5:420}
\theta( \Bx, \mu ) + (1-\theta) (\By, \nu) =
(\theta \Bx (1-\theta) \By, \theta \mu (1-\theta) \nu )
\in \textrm{epi} F,
\end{equation}

since \( \textrm{epi} F \) is a convex set.

By definition of \( \textrm{epi} F \)

\begin{equation}\label{eqn:convexOptimizationLecture5:440}
F( \theta \Bx (1-\theta) \By ) \le \theta \mu (1-\theta) \nu.
\end{equation}

Picking \( \mu = F(\Bx), \nu = F(\By) \) gives
\begin{equation}\label{eqn:convexOptimizationLecture5:460}
F( \theta \Bx (1-\theta) \By ) \le \theta F(\Bx) (1-\theta) F(\By).
\end{equation}

Extended value function

Sometimes convenient to work with “extended value function”

\begin{equation}\label{eqn:convexOptimizationLecture5:500}
\tilde{F}(\Bx) =
\left\{
\begin{array}{l l}
F(\Bx) & \quad \mbox{If \( \Bx \in \textrm{dom} F\)} \\
\infty & \quad \mbox{otherwise.}
\end{array}
\right.
\end{equation}

Examples:

  • Linear (affine) functions (fig. 8) are both convex and concave.

    fig. 8. Linear functions.

  • \( x^2 \) is convex, sketched in fig. 9.

    fig. 9. Convex (quadratic.)

  • \( \log x, \textrm{dom} F = \mathbb{R}_{+} \) concave, sketched in fig. 10.

    fig. 10. Concave (logarithm.)

  • \( \Norm{\Bx} \) is convex. \( \Norm{ \theta \Bx + (1-\theta) \By } \le \theta \Norm{ \Bx } + (1-\theta) \Norm{\By } \).
  • \( 1/x \) is convex on \( \setlr{ x | x > 0 } = \textrm{dom} F \), and concave on \( \setlr{ x | x < 0 } = \textrm{dom} F \). \begin{equation}\label{eqn:convexOptimizationLecture5:520} \tilde{F}(x) = \left\{ \begin{array}{l l} \inv{x} & \quad \mbox{If \( x > 0 \)} \\
    \infty & \quad \mbox{else.}
    \end{array}
    \right.
    \end{equation}

Definition: Sublevel

The sublevel set of a function \( F : \mathbb{R}^n \rightarrow \mathbb{R} \) is

\begin{equation*}
C(\alpha) = \setlr{ \Bx \in \textrm{dom} F | F(\Bx) \le \alpha }
\end{equation*}

 

Convex sublevel

 

Non-convex sublevel.

Theorem:
If \( F \) is convex then \( C(\alpha) \) is a convex set \( \forall \alpha \).

This is not an if and only if condition, as illustrated in fig. 12.

 

fig. 12. Convex sublevel does not imply convexity.

There \( C(\alpha) \) is convex, but the function itself is not.

Proof:

Since \( F \) is convex, then \( \textrm{epi} F \) is a convex set.

  • Let\begin{equation}\label{eqn:convexOptimizationLecture5:580}
    \mathcal{A} = \setlr{ (\Bx,t) | t = \alpha }
    \end{equation}is a convex set.
  • \( \mathcal{A} \cap \textrm{epi} F \)is a convex set since it is the intersection of convex sets.
  • Project \( \mathcal{A} \cap \textrm{epi} F \) onto \R{n} (i.e. domain of \( F \) ). The projection is an affine mapping. Image of a convex set through affine mapping is a convex set.

Definition: Quasi-convex.

A function is quasi-convex if \underline{all} of its sublevel sets are convex.

Composing convex functions

Properties of convex functions:

  • If \( F \) is convex, then \( \alpha F \) is convex \( \forall \alpha > 0 \).
  • If \( F_1, F_2 \) are convex, then the sum \( F_1 + F_2 \) is convex.
  • If \( F \) is convex, then \( g(\Bx) = F(A \Bx + \Bb) \) is convex \( \forall \Bx \in \setlr{ \Bx | A \Bx + \Bb \in \textrm{dom} F } \).

Note: for the last

\begin{equation}\label{eqn:convexOptimizationLecture5:620}
\begin{aligned}
g &: \mathbb{R}^m \rightarrow \mathbb{R} \\
F &: \mathbb{R}^n \rightarrow \mathbb{R} \\
\Bx &\in \mathbb{R}^m \\
A &\in \mathbb{R}^{n \times m} \\
\Bb &\in \mathbb{R}^n
\end{aligned}
\end{equation}

Proof (of last):

\begin{equation}\label{eqn:convexOptimizationLecture5:640}
\begin{aligned}
g( \theta \Bx + (1-\theta) \By )
&=
F( \theta (A \Bx + \Bb) + (1-\theta) (A \By + \Bb) ) \\
&\le
\theta F( A \Bx + \Bb) + (1-\theta) F (A \By + \Bb) \\
&= \theta g(\Bx) + (1-\theta) g(\By).
\end{aligned}
\end{equation}

References

[1] Stephen Boyd and Lieven Vandenberghe. Convex optimization. Cambridge university press, 2004.