rejection

Shortest distance between lines

December 14, 2024 math and physics play 2 comments , , , , , , ,

[Click here for a PDF version of this post]

Motivation.

Having just worked one of Karl’s problems for the distance between two parallel planes, I recalled that when I was in high school, I had trouble with the intuition for the problem of shortest distance between two lines.

In this post, I’ll revisit that ancient trouble and finally come to terms with it.

Distance from origin to a line.

Before doing the two lines problem, let’s look at a similar simpler problem, the shortest distance from the origin to a line. The parametric representation of a line going through point \( \Bp \) with (unit) direction vector \( \mathbf{\hat{d}} \) is
\begin{equation}\label{eqn:shortestDistanceBetweenLines:40}
L: \Bx(r) = \Bp + r \mathbf{\hat{d}}.
\end{equation}
If we want to solve this the dumb but mechanical way, we have only to minimize a length-squared function for the distance to a point on the line
\begin{equation}\label{eqn:shortestDistanceBetweenLines:60}
\begin{aligned}
D
&= \Norm{\Bx}^2 \\
&= \Bp^2 + r^2 + 2 r \Bp \cdot \mathbf{\hat{d}}.
\end{aligned}
\end{equation}
The minimum will occur where the first derivative is zero
\begin{equation}\label{eqn:shortestDistanceBetweenLines:80}
\begin{aligned}
0
&= \PD{r}{D} \\
&= 2 r + 2 \Bp \cdot \mathbf{\hat{d}},
\end{aligned}
\end{equation}
so at the minimum we have
\begin{equation}\label{eqn:shortestDistanceBetweenLines:100}
r = -\Bp \cdot \mathbf{\hat{d}}.
\end{equation}
This means the vector to the nearest point on the line is
\begin{equation}\label{eqn:shortestDistanceBetweenLines:120}
\begin{aligned}
\Bx
&= \Bp – \lr{ \Bp \cdot \mathbf{\hat{d}} }\mathbf{\hat{d}} \\
&= \Bp \mathbf{\hat{d}}^2 – \lr{ \Bp \cdot \mathbf{\hat{d}}}\mathbf{\hat{d}} \\
&= \lr{ \Bp \wedge \mathbf{\hat{d}} } \mathbf{\hat{d}},
\end{aligned}
\end{equation}
or for \(\mathbb{R}^3\)
\begin{equation}\label{eqn:shortestDistanceBetweenLines:140}
\Bx
= -\lr{ \Bp \cross \mathbf{\hat{d}} } \cross \mathbf{\hat{d}}.
\end{equation}

fig. 1. Directed distance from origin to line.

The geometry of the problem is illustrated in fig. 1.

Observe that all the calculation above was superfluous, as observation of the geometry shows that we just wanted the rejection of \( \mathbf{\hat{d}} \) (green) from \( \Bp \) (blue), and could have stated the result directly.

Distance between two lines.

Suppose that we have two lines, specified with a point and direction vector for each line, as illustrated in fig. 2
\begin{equation}\label{eqn:shortestDistanceBetweenLines:20}
\begin{aligned}
L_1&: \Bx(r) = \Bp_1 + r \mathbf{\hat{d}}_1 \\
L_2&: \Bx(s) = \Bp_2 + s \mathbf{\hat{d}}_2 \\
\end{aligned}
\end{equation}

fig. 2. Two lines, not intersecting.

 

The geometry of the problem becomes more clear if we augment this figure, adding a line with the direction \( \mathbf{\hat{d}}_2 \) to \( L_1 \), and adding a line with the direction \( \mathbf{\hat{d}}_1 \) to \( L_2 \), as illustrated in fig. 3, and then visually extending each of those lines to planes that pass through the respective points. We can now rotate our viewpoint so that we look at those planes on edge, which shows that the problem to solve is really just the distance between two parallel planes.

fig 3a. Augmenting the lines with alternate direction vectors to form planes.

fig 3b. Rotation to view planes edge on.

The equations of these planes are just
\begin{equation}\label{eqn:shortestDistanceBetweenLines:160}
\begin{aligned}
P_1&: \Bx(r, s) = \Bp_1 + r \mathbf{\hat{d}}_1 + s \mathbf{\hat{d}}_2 \\
P_2&: \Bx(t, u) = \Bp_2 + t \mathbf{\hat{d}}_2 + u \mathbf{\hat{d}}_1,
\end{aligned}
\end{equation}
or with
\begin{equation}\label{eqn:shortestDistanceBetweenLines:180}
\mathbf{\hat{n}} = \frac{\mathbf{\hat{d}}_1 \cross \mathbf{\hat{d}}_2}{\Norm{\mathbf{\hat{d}}_1 \cross \mathbf{\hat{d}}_2}},
\end{equation}
the normal form for these planes are
\begin{equation}\label{eqn:shortestDistanceBetweenLines:200}
\begin{aligned}
P_1&: \Bx \cdot \mathbf{\hat{n}} = \Bp_1 \cdot \mathbf{\hat{n}} \\
P_2&: \Bx \cdot \mathbf{\hat{n}} = \Bp_2 \cdot \mathbf{\hat{n}}.
\end{aligned}
\end{equation}
Now we can state the distance between the planes trivially, using the results from our previous posts, finding
\begin{equation}\label{eqn:shortestDistanceBetweenLines:220}
d = \Abs{ \Bp_2 \cdot \mathbf{\hat{n}} – \Bp_1 \cdot \mathbf{\hat{n}} },
\end{equation}
or, encoding the triple product in it’s determinant form, the shortest distance between the lines (up to a sign), is
\begin{equation}\label{eqn:shortestDistanceBetweenLines:240}
\boxed{
d = \frac{
\begin{vmatrix}
\Bp_2 – \Bp_1 & \mathbf{\hat{d}}_1 & \mathbf{\hat{d}}_2
\end{vmatrix}
}{
\Norm{ \mathbf{\hat{d}}_1 \cross \mathbf{\hat{d}}_2 }
}.
}
\end{equation}

As a minimization problem.

Trying this as a minimization problem is actually kind of fun, albeit messy. Doing that calculation will give us the directed shortest distance between the lines.
We can form any number of vectors \( \Bm \) connecting the two lines
\begin{equation}\label{eqn:shortestDistanceBetweenLines:260}
\Bp_1 + s \mathbf{\hat{d}}_1 + \Bm = \Bp_2 + t \mathbf{\hat{d}}_2,
\end{equation}
or, with \( \Delta = \Bp_2 – \Bp_1 \), that directed distance is
\begin{equation}\label{eqn:shortestDistanceBetweenLines:280}
\Bm = \Delta + t \mathbf{\hat{d}}_2 – s \mathbf{\hat{d}}_1.
\end{equation}
We seek to minimize the squared length of this vector
\begin{equation}\label{eqn:shortestDistanceBetweenLines:300}
D = \Norm{\Bm}^2 = \Delta^2 + \lr{ t \mathbf{\hat{d}}_2 – s \mathbf{\hat{d}}_1 }^2 + 2 \Delta \cdot \lr{ t \mathbf{\hat{d}}_2 – s \mathbf{\hat{d}}_1 }.
\end{equation}
The minimization constraints are
\begin{equation}\label{eqn:shortestDistanceBetweenLines:320}
\begin{aligned}
0 &= \PD{s}{D} = 2 \lr{ t \mathbf{\hat{d}}_2 – s \mathbf{\hat{d}}_1 } \cdot \lr{ -\mathbf{\hat{d}}_1 } + 2 \Delta \cdot \lr{ – \mathbf{\hat{d}}_1 } \\
0 &= \PD{t}{D} = 2 \lr{ t \mathbf{\hat{d}}_2 – s \mathbf{\hat{d}}_1 } \cdot \lr{ \mathbf{\hat{d}}_2 } + 2 \Delta \cdot \lr{ \mathbf{\hat{d}}_2 }.
\end{aligned}
\end{equation}
With \( \alpha = \mathbf{\hat{d}}_1 \cdot \mathbf{\hat{d}}_2 \), our solution for \( s, t \) is
\begin{equation}\label{eqn:shortestDistanceBetweenLines:340}
\begin{bmatrix}
s \\
t
\end{bmatrix}
=
{
\begin{bmatrix}
1 & -\alpha \\
-\alpha & 1
\end{bmatrix}
}^{-1}
\begin{bmatrix}
\Delta \cdot \mathbf{\hat{d}}_1 \\
-\Delta \cdot \mathbf{\hat{d}}_2 \\
\end{bmatrix},
\end{equation}
so
\begin{equation}\label{eqn:shortestDistanceBetweenLines:360}
\begin{aligned}
t \mathbf{\hat{d}}_2 – s \mathbf{\hat{d}}_1
&=
\begin{bmatrix}
-\mathbf{\hat{d}}_1 & \mathbf{\hat{d}}_2
\end{bmatrix}
\begin{bmatrix}
s \\
t
\end{bmatrix} \\
&=
\inv{1 – \alpha^2}
\begin{bmatrix}
-\mathbf{\hat{d}}_1 & \mathbf{\hat{d}}_2
\end{bmatrix}
\begin{bmatrix}
1 & \alpha \\
\alpha & 1
\end{bmatrix}
\begin{bmatrix}
\Delta \cdot \mathbf{\hat{d}}_1 \\
-\Delta \cdot \mathbf{\hat{d}}_2 \\
\end{bmatrix} \\
&=
\inv{1 – \alpha^2}
\begin{bmatrix}
-\mathbf{\hat{d}}_1 & \mathbf{\hat{d}}_2
\end{bmatrix}
\begin{bmatrix}
\Delta \cdot \mathbf{\hat{d}}_1 – \alpha \Delta \cdot \mathbf{\hat{d}}_2 \\
\alpha \Delta \cdot \mathbf{\hat{d}}_1 -\Delta \cdot \mathbf{\hat{d}}_2 \\
\end{bmatrix} \\
&=
\inv{1 – \alpha^2}
\lr{
-\lr{ \Delta \cdot \mathbf{\hat{d}}_1} \mathbf{\hat{d}}_1 + \alpha \lr{ \Delta \cdot \mathbf{\hat{d}}_2} \mathbf{\hat{d}}_1
+
\alpha \lr{ \Delta \cdot \mathbf{\hat{d}}_1} \mathbf{\hat{d}}_2 – \lr{ \Delta \cdot \mathbf{\hat{d}}_2} \mathbf{\hat{d}}_2
} \\
&=
\inv{1 – \alpha^2}
\lr{
\lr{ \Delta \cdot \mathbf{\hat{d}}_1} \lr{
-\mathbf{\hat{d}}_1 + \alpha \mathbf{\hat{d}}_2
}
+
\lr{ \Delta \cdot \mathbf{\hat{d}}_2} \lr{
-\mathbf{\hat{d}}_2 + \alpha \mathbf{\hat{d}}_1
}
}.
\end{aligned}
\end{equation}
This might look a bit hopeless to simplify, but note that
\begin{equation}\label{eqn:shortestDistanceBetweenLines:380}
\begin{aligned}
\lr{ \mathbf{\hat{d}}_1 \wedge \mathbf{\hat{d}}_2}^2
&=
\lr{ \mathbf{\hat{d}}_1 \wedge \mathbf{\hat{d}}_2} \cdot \lr{ \mathbf{\hat{d}}_1 \wedge \mathbf{\hat{d}}_2} \\
&=
\mathbf{\hat{d}}_1 \cdot \lr{ \mathbf{\hat{d}}_2 \cdot \lr{ \mathbf{\hat{d}}_1 \wedge \mathbf{\hat{d}}_2} } \\
&=
\mathbf{\hat{d}}_1 \cdot \lr{ \alpha \mathbf{\hat{d}}_2 – \mathbf{\hat{d}}_1 } \\
&=
\alpha^2 – 1,
\end{aligned}
\end{equation}
and
\begin{equation}\label{eqn:shortestDistanceBetweenLines:400}
\begin{aligned}
\mathbf{\hat{d}}_2 \cdot \lr{ \mathbf{\hat{d}}_1 \wedge \mathbf{\hat{d}}_2} &= \alpha \mathbf{\hat{d}}_2 – \mathbf{\hat{d}}_1 \\
-\mathbf{\hat{d}}_1 \cdot \lr{ \mathbf{\hat{d}}_1 \wedge \mathbf{\hat{d}}_2} &= -\mathbf{\hat{d}}_2 + \alpha \mathbf{\hat{d}}_1.
\end{aligned}
\end{equation}
Let’s write \( B = \mathbf{\hat{d}}_1 \wedge \mathbf{\hat{d}}_2 \), and plug in our bivector expressions
\begin{equation}\label{eqn:shortestDistanceBetweenLines:420}
\begin{aligned}
t \mathbf{\hat{d}}_2 – s \mathbf{\hat{d}}_1
&=
-\inv{B^2}
\lr{
\lr{ \Delta \cdot \mathbf{\hat{d}}_1} \mathbf{\hat{d}}_2 \cdot B
-\lr{ \Delta \cdot \mathbf{\hat{d}}_2} \mathbf{\hat{d}}_1 \cdot B
} \\
&=
-\inv{B^2}
\lr{
\lr{ \Delta \cdot \mathbf{\hat{d}}_1} \mathbf{\hat{d}}_2
-\lr{ \Delta \cdot \mathbf{\hat{d}}_2} \mathbf{\hat{d}}_1
}
\cdot B \\
&=
-\inv{B^2}
\lr{
\Delta \cdot \lr{ \mathbf{\hat{d}}_1 \wedge \mathbf{\hat{d}}_2}
}
\cdot B \\
&=
-\inv{B^2} \lr{ \Delta \cdot B } \cdot B \\
&=
-\inv{B^2} \gpgradeone{ \lr{ \Delta \cdot B } B } \\
&=
-\inv{B^2} \gpgradeone{ \lr{ \Delta B – \Delta \wedge B } B } \\
&=
-\Delta + \inv{B^2} \lr{ \Delta \wedge B } \cdot B.
\end{aligned}
\end{equation}
The minimum directed distance between the lines is now reduced to just
\begin{equation}\label{eqn:shortestDistanceBetweenLines:440}
\begin{aligned}
\Bm
&= \Delta + t \mathbf{\hat{d}}_2 – s \mathbf{\hat{d}}_1 \\
&= \lr{ \Delta \wedge B } \inv{B}.
\end{aligned}
\end{equation}
Again, had we used the geometry effectively, illustrated in fig. 4, we could have skipped directly to this result. This is the rejection of the plane \( B \) from \( \Delta \), that is, rejection of both \( \mathbf{\hat{d}}_1, \mathbf{\hat{d}}_2 \) from the difference \( \Bp_2 – \Bp_1 \), leaving just the perpendicular shortest connector between the lines.

fig. 4. Projection onto the normal to the parallel planes.

We can also conceptualize this as computing the trivector volume (parallelepiped with edges \( \Bp_2 – \Bp_1, \mathbf{\hat{d}}_1, \mathbf{\hat{d}}_2 \)), and then dividing out the bivector (parallelogram with edges \(\mathbf{\hat{d}}_1, \mathbf{\hat{d}}_2 \)), to find the vector (height) of the parallelepiped.

Observe that rejecting from the plane, is equivalent to projecting onto the normal, so for \(\mathbb{R}^3\) we may translate this to conventional vector algebra, as a projection
\begin{equation}\label{eqn:shortestDistanceBetweenLines:500}
\Bm = \lr{\Delta \cdot \mathbf{\hat{n}}} \mathbf{\hat{n}},
\end{equation}
where \( \mathbf{\hat{n}} = \lr{ \mathbf{\hat{d}}_1 \cross \mathbf{\hat{d}}_2 }/\Norm{\mathbf{\hat{d}}_1 \cross \mathbf{\hat{d}}_2 } \).

If we want the magnitude of this vector, it’s just
\begin{equation}\label{eqn:shortestDistanceBetweenLines:480}
\begin{aligned}
\Norm{\Bm}^2
&=
\inv{B^4} \lr{ \lr{ \Delta \wedge B } B } \lr{ B \lr{ B \wedge \Delta } } \\
&=
\inv{B^2} \lr{ \Delta \wedge B }^2,
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:shortestDistanceBetweenLines:460}
\boxed{
\Norm{\Bm} = \frac{ \Norm{ \lr{\Bp_2 – \Bp_1} \wedge \mathbf{\hat{d}}_1 \wedge \mathbf{\hat{d}}_2 } }{ \Norm{\mathbf{\hat{d}}_1 \wedge \mathbf{\hat{d}}_2} },
}
\end{equation}
which, for \(\mathbb{R}^3\), is equivalent to the triple product result we found above.

Radial vector representation, momentum, and angular momentum.

September 8, 2023 math and physics play , , , , , ,

[Click here for a PDF version of this post], and here for a video version of this post.

 

Motivation.

In my last couple GA YouTube videos, circular and spherical coordinates were examined.

This post is a text representation of a new video that follows up on those two videos.

We found the form of the unit vector derivatives in both cases.

\begin{equation}\label{eqn:radialderivatives:20}
\Bx = r \mathbf{\hat{r}},
\end{equation}
leaving the angular dependence of \( \mathbf{\hat{r}} \) unspecified. We want to find both \( \Bv = \Bx’ \) and \( \mathbf{\hat{r}}’\).

Derivatives.

Lemma 1.1: Radial length derivative.

The derivative of a spherical length \( r \) can be expressed as
\begin{equation*}
\frac{dr}{dt} = \mathbf{\hat{r}} \cdot \frac{d\Bx}{dt}.
\end{equation*}

Start proof:

We write \( r^2 = \Bx \cdot \Bx \), and take derivatives of both sides, to find
\begin{equation}\label{eqn:radialderivatives:60}
2 r \frac{dr}{dt} = 2 \Bx \cdot \frac{d\Bx}{dt},
\end{equation}
or
\begin{equation}\label{eqn:radialderivatives:80}
\frac{dr}{dt} = \frac{\Bx}{r} \cdot \frac{d\Bx}{dt} = \mathbf{\hat{r}} \cdot \frac{d\Bx}{dt}.
\end{equation}

End proof.

Application of the chain rule to \ref{eqn:radialderivatives:20} is straightforward
\begin{equation}\label{eqn:radialderivatives:100}
\Bx’ = r’ \mathbf{\hat{r}} + r \mathbf{\hat{r}}’,
\end{equation}
but we don’t know the form for \( \mathbf{\hat{r}}’ \). We could proceed with a niave expansion of
\begin{equation}\label{eqn:radialderivatives:120}
\frac{d}{dt} \lr{ \frac{\Bx}{r} },
\end{equation}
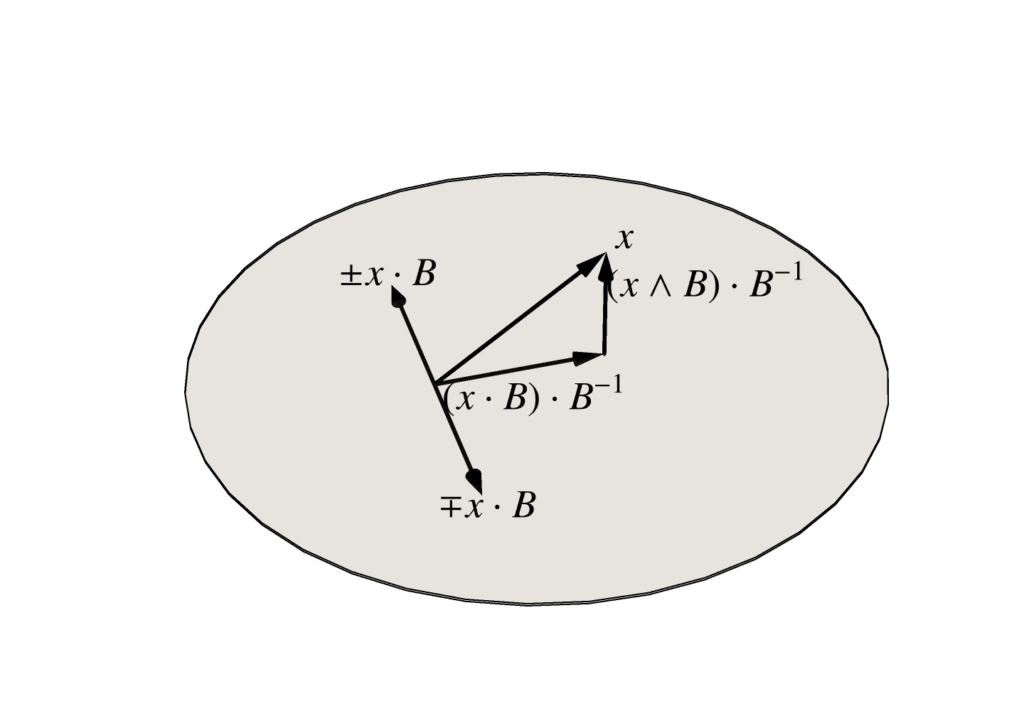
but we can be sneaky, and perform a projective and rejective split of \( \Bx’ \) with respect to \( \mathbf{\hat{r}} \). That is
\begin{equation}\label{eqn:radialderivatives:140}
\begin{aligned}
\Bx’
&= \mathbf{\hat{r}} \mathbf{\hat{r}} \Bx’ \\
&= \mathbf{\hat{r}} \lr{ \mathbf{\hat{r}} \Bx’ } \\
&= \mathbf{\hat{r}} \lr{ \mathbf{\hat{r}} \cdot \Bx’ + \mathbf{\hat{r}} \wedge \Bx’} \\
&= \mathbf{\hat{r}} \lr{ r’ + \mathbf{\hat{r}} \wedge \Bx’}.
\end{aligned}
\end{equation}
We used our lemma in the last step above, and after distribution, find
\begin{equation}\label{eqn:radialderivatives:160}
\Bx’ = r’ \mathbf{\hat{r}} + \mathbf{\hat{r}} \lr{ \mathbf{\hat{r}} \wedge \Bx’ }.
\end{equation}
Comparing to \ref{eqn:radialderivatives:100}, we see that
\begin{equation}\label{eqn:radialderivatives:180}
r \mathbf{\hat{r}}’ = \mathbf{\hat{r}} \lr{ \mathbf{\hat{r}} \wedge \Bx’ }.
\end{equation}
We see that the radial unit vector derivative is proportional to the rejection of \( \mathbf{\hat{r}} \) from \( \Bx’ \)
\begin{equation}\label{eqn:radialderivatives:200}
\mathbf{\hat{r}}’ = \inv{r} \mathrm{Rej}_{\mathbf{\hat{r}}}(\Bx’) = \inv{r^3} \Bx \lr{ \Bx \wedge \Bx’ }.
\end{equation}
The vector \( \mathbf{\hat{r}}’ \) is perpendicular to \( \mathbf{\hat{r}} \) for any parameterization of it’s orientation, or in symbols
\begin{equation}\label{eqn:radialderivatives:220}
\mathbf{\hat{r}} \cdot \mathbf{\hat{r}}’ = 0.
\end{equation}
We saw this for the circular and spherical parameterizations, and see now that this also holds more generally.

Angular momentum.

Let’s now write out the momentum \( \Bp = m \Bv \) for a point particle with mass \( m \), and determine the kinetic energy \( m \Bv^2/2 = \Bp^2/2m \) for that particle.

The momentum is
\begin{equation}\label{eqn:radialderivatives:320}
\begin{aligned}
\Bp
&= m r’ \mathbf{\hat{r}} + m \mathbf{\hat{r}} \lr{ \mathbf{\hat{r}} \wedge \Bv } \\
&= m r’ \mathbf{\hat{r}} + \inv{r} \mathbf{\hat{r}} \lr{ \Br \wedge \Bp }.
\end{aligned}
\end{equation}
Observe that \( p_r = m r’ \) is the radial component of the momentum. It is natural to introduce a bivector valued angular momentum operator
\begin{equation}\label{eqn:radialderivatives:340}
L = \Br \wedge \Bp,
\end{equation}
splitting the momentum into a component that is strictly radial and a component that lies purely on the surface of a spherical surface in momentum space. That is
\begin{equation}\label{eqn:radialderivatives:360}
\Bp = p_r \mathbf{\hat{r}} + \inv{r} \mathbf{\hat{r}} L.
\end{equation}
Making use of the fact that \( \mathbf{\hat{r}} \) and \( \mathrm{Rej}_{\mathbf{\hat{r}}}(\Bx’) \) are perpendicular (so there are no cross terms when we square the momentum), the
kinetic energy is
\begin{equation}\label{eqn:radialderivatives:380}
\begin{aligned}
\inv{2m} \Bp^2
&= \inv{2m} \lr{ p_r \mathbf{\hat{r}} + \inv{r} \mathbf{\hat{r}} L }^2 \\
&= \inv{2m} p_r^2 + \inv{2 m r^2 } \mathbf{\hat{r}} L \mathbf{\hat{r}} L \\
&= \inv{2m} p_r^2 – \inv{2 m r^2 } \mathbf{\hat{r}} L^2 \mathbf{\hat{r}} \\
&= \inv{2m} p_r^2 – \inv{2 m r^2 } L^2 \mathbf{\hat{r}}^2,
\end{aligned}
\end{equation}
where we’ve used the anticommutative nature of \( \mathbf{\hat{r}} \) and \( L \) (i.e.: a sign swap is needed to swap them), and used the fact that \( L^2 \) is a scalar, allowing us to commute \( \mathbf{\hat{r}} \) with \( L^2 \). This leaves us with
\begin{equation}\label{eqn:radialderivatives:400}
E = \inv{2m} \Bp^2 = \inv{2m} p_r^2 – \inv{2 m r^2 } L^2.
\end{equation}
Observe that both the radial momentum term and the angular momentum term are both strictly postive, since \( L \) is a bivector and \( L^2 \le 0 \).

Problems.

Problem:

Find \ref{eqn:radialderivatives:200} without being sneaky.

Answer

\begin{equation}\label{eqn:radialderivatives:280}
\begin{aligned}
\mathbf{\hat{r}}’
&= \frac{d}{dt} \lr{ \frac{\Bx}{r} } \\
&= \inv{r} \Bx’ – \inv{r^2} \Bx r’ \\
&= \inv{r} \Bx’ – \inv{r} \mathbf{\hat{r}} r’ \\
&= \inv{r} \lr{ \Bx’ – \mathbf{\hat{r}} r’ } \\
&= \inv{r} \lr{ \mathbf{\hat{r}} \mathbf{\hat{r}} \Bx’ – \mathbf{\hat{r}} r’ } \\
&= \inv{r} \mathbf{\hat{r}} \lr{ \mathbf{\hat{r}} \Bx’ – r’ } \\
&= \inv{r} \mathbf{\hat{r}} \lr{ \mathbf{\hat{r}} \Bx’ – \mathbf{\hat{r}} \cdot \Bx’ } \\
&= \inv{r} \mathbf{\hat{r}} \lr{ \mathbf{\hat{r}} \wedge \Bx’ }.
\end{aligned}
\end{equation}

Problem:

Show that \ref{eqn:radialderivatives:200} can be expressed as a triple vector cross product
\begin{equation}\label{eqn:radialderivatives:230}
\mathbf{\hat{r}}’ = \inv{r^3} \lr{ \Bx \cross \Bx’ } \cross \Bx,
\end{equation}

Answer

While this may be familiar from elementary calculus, such as in [1], we can show follows easily from our GA result
\begin{equation}\label{eqn:radialderivatives:300}
\begin{aligned}
\mathbf{\hat{r}}’
&= \inv{r} \mathbf{\hat{r}} \lr{ \mathbf{\hat{r}} \wedge \Bx’ } \\
&= \inv{r} \gpgradeone{ \mathbf{\hat{r}} \lr{ \mathbf{\hat{r}} \wedge \Bx’ } } \\
&= \inv{r} \gpgradeone{ \mathbf{\hat{r}} I \lr{ \mathbf{\hat{r}} \cross \Bx’ } } \\
&= \inv{r} \gpgradeone{ I \lr{ \mathbf{\hat{r}} \cdot \lr{ \mathbf{\hat{r}} \cross \Bx’ } + \mathbf{\hat{r}} \wedge \lr{ \mathbf{\hat{r}} \cross \Bx’ } } } \\
&= \inv{r} \gpgradeone{ I^2 \mathbf{\hat{r}} \cross \lr{ \mathbf{\hat{r}} \cross \Bx’ } } \\
&= \inv{r} \lr{ \mathbf{\hat{r}} \cross \Bx’ } \cross \mathbf{\hat{r}}.
\end{aligned}
\end{equation}

References

[1] S.L. Salas and E. Hille. Calculus: one and several variables. Wiley New York, 1990.

New video: Velocity and angular momentum with geometric algebra

September 7, 2023 math and physics play , , , , ,

 

In this video, we compute velocity in a radial representation \( \mathbf{x} = r \mathbf{\hat{r}} \).

We use a scalar radial coordinate \( r \), and leave all the angular dependence implicitly encoded in a radial unit vector \( \mathbf{\hat{r}} \).

We find the geometric algebra structure of the \( \mathbf{\hat{r}}’ \) in two different ways, to find

\( \mathbf{\hat{r}}’ = \frac{\mathbf{\hat{r}}}{r} \left( \mathbf{\hat{r}} \wedge \mathbf{\hat{x}}’ \right), \)

then derive the conventional triple vector cross product equivalent for reference:

\( \mathbf{\hat{r}}’ = \left( \mathbf{\hat{r}} \times \mathbf{\hat{x}}’ \right) \times \frac{\mathbf{\hat{r}}}{r}. \)

We then compute kinetic energy in this representation, and show how a bivector-valued angular momentum \( L = \mathbf{x} \wedge \mathbf{p} \), falls naturally from that computation, where we have

\( \frac{m}{2} \mathbf{v}^2 = \frac{1}{2 m} {(m r’)}^2 – \frac{1}{2 m r^2 } L^2. \)

Prerequisites: calculus (derivatives and chain rule), and geometric algebra basics (vector multiplication, commutation relationships for vectors and bivectors in a plane, wedge and cross product equivalencies, …)

Errata: at around 4:12 I used \( \mathbf{r} \) instead of \( \mathbf{x} \), then kept doing so every time after that when the value for \( L \) was stated.

As well as being posted to Google’s censorship-tube, this video can also be found on odysee.

Lorentz transformations in Space Time Algebra (STA)

December 12, 2020 math and physics play , , , , , , , , , , , , , , , , , ,

[If mathjax doesn’t display properly for you, click here for a PDF of this post]

Motivation.

One of the remarkable features of geometric algebra are the complex exponential sandwiches that can be used to encode rotations in any dimension, or rotation like operations like Lorentz transformations in Minkowski spaces. In this post, we show some examples that unpack the geometric algebra expressions for Lorentz transformations operations of this sort. In particular, we will look at the exponential sandwich operations for spatial rotations and Lorentz boosts in the Dirac algebra, known as Space Time Algebra (STA) in geometric algebra circles, and demonstrate that these sandwiches do have the desired effects.

Lorentz transformations.

Theorem 1.1: Lorentz transformation.

The transformation
\begin{equation}\label{eqn:lorentzTransform:580}
x \rightarrow e^{B} x e^{-B} = x’,
\end{equation}
where \( B = a \wedge b \), is an STA 2-blade for any two linearly independent four-vectors \( a, b \), is a norm preserving, that is
\begin{equation}\label{eqn:lorentzTransform:600}
x^2 = {x’}^2.
\end{equation}

Start proof:

The proof is disturbingly trivial in this geometric algebra form
\begin{equation}\label{eqn:lorentzTransform:40}
\begin{aligned}
{x’}^2
&=
e^{B} x e^{-B} e^{B} x e^{-B} \\
&=
e^{B} x x e^{-B} \\
&=
x^2 e^{B} e^{-B} \\
&=
x^2.
\end{aligned}
\end{equation}

End proof.

In particular, observe that we did not need to construct the usual infinitesimal representations of rotation and boost transformation matrices or tensors in order to demonstrate that we have spacetime invariance for the transformations. The rough idea of such a transformation is that the exponential commutes with components of the four-vector that lie off the spacetime plane specified by the bivector \( B \), and anticommutes with components of the four-vector that lie in the plane. The end result is that the sandwich operation simplifies to
\begin{equation}\label{eqn:lorentzTransform:60}
x’ = x_\parallel e^{-B} + x_\perp,
\end{equation}
where \( x = x_\perp + x_\parallel \) and \( x_\perp \cdot B = 0 \), and \( x_\parallel \wedge B = 0 \). In particular, using \( x = x B B^{-1} = \lr{ x \cdot B + x \wedge B } B^{-1} \), we find that
\begin{equation}\label{eqn:lorentzTransform:80}
\begin{aligned}
x_\parallel &= \lr{ x \cdot B } B^{-1} \\
x_\perp &= \lr{ x \wedge B } B^{-1}.
\end{aligned}
\end{equation}
When \( B \) is a spacetime plane \( B = b \wedge \gamma_0 \), then this exponential has a hyperbolic nature, and we end up with a Lorentz boost. When \( B \) is a spatial bivector, we end up with a single complex exponential, encoding our plane old 3D rotation. More general \( B \)’s that encode composite boosts and rotations are also possible, but \( B \) must be invertible (it should have no lightlike factors.) The rough geometry of these projections is illustrated in fig 1, where the spacetime plane is represented by \( B \).

Projection and rejection geometry.

fig 1. Projection and rejection geometry.

 

What is not so obvious is how to pick \( B \)’s that correspond to specific rotation axes or boost directions. Let’s consider each of those cases in turn.

Theorem 1.2: Boost.

The boost along a direction vector \( \vcap \) and rapidity \( \alpha \) is given by
\begin{equation}\label{eqn:lorentzTransform:620}
x’ = e^{-\vcap \alpha/2} x e^{\vcap \alpha/2},
\end{equation}
where \( \vcap = \gamma_{k0} \cos\theta^k \) is an STA bivector representing a spatial direction with direction cosines \( \cos\theta^k \).

Start proof:

We want to demonstrate that this is equivalent to the usual boost formulation. We can start with decomposition of the four-vector \( x \) into components that lie in and off of the spacetime plane \( \vcap \).
\begin{equation}\label{eqn:lorentzTransform:100}
\begin{aligned}
x
&= \lr{ x^0 + \Bx } \gamma_0 \\
&= \lr{ x^0 + \Bx \vcap^2 } \gamma_0 \\
&= \lr{ x^0 + \lr{ \Bx \cdot \vcap} \vcap + \lr{ \Bx \wedge \vcap} \vcap } \gamma_0,
\end{aligned}
\end{equation}
where \( \Bx = x \wedge \gamma_0 \). The first two components lie in the boost plane, whereas the last is the spatial component of the vector that lies perpendicular to the boost plane. Observe that \( \vcap \) anticommutes with the dot product term and commutes with he wedge product term, so we have
\begin{equation}\label{eqn:lorentzTransform:120}
\begin{aligned}
x’
&=
\lr{ x^0 + \lr{ \Bx \cdot \vcap } \vcap } \gamma_0
e^{\vcap \alpha/2 }
e^{\vcap \alpha/2 }
+
\lr{ \Bx \wedge \vcap } \vcap \gamma_0
e^{-\vcap \alpha/2 }
e^{\vcap \alpha/2 } \\
&=
\lr{ x^0 + \lr{ \Bx \cdot \vcap } \vcap } \gamma_0
e^{\vcap \alpha }
+
\lr{ \Bx \wedge \vcap } \vcap \gamma_0.
\end{aligned}
\end{equation}
Noting that \( \vcap^2 = 1 \), we may expand the exponential in hyperbolic functions, and find that the boosted portion of the vector expands as
\begin{equation}\label{eqn:lorentzTransform:260}
\begin{aligned}
\lr{ x^0 + \lr{ \Bx \cdot \vcap} \vcap } \gamma_0 e^{\vcap \alpha}
&=
\lr{ x^0 + \lr{ \Bx \cdot \vcap} \vcap } \gamma_0 \lr{ \cosh\alpha + \vcap \sinh \alpha} \\
&=
\lr{ x^0 + \lr{ \Bx \cdot \vcap} \vcap } \lr{ \cosh\alpha – \vcap \sinh \alpha} \gamma_0 \\
&=
\lr{ x^0 \cosh\alpha – \lr{ \Bx \cdot \vcap} \sinh \alpha} \gamma_0
+
\lr{ -x^0 \sinh \alpha + \lr{ \Bx \cdot \vcap} \cosh \alpha } \vcap \gamma_0.
\end{aligned}
\end{equation}
We are left with
\begin{equation}\label{eqn:lorentzTransform:320}
\begin{aligned}
x’
&=
\lr{ x^0 \cosh\alpha – \lr{ \Bx \cdot \vcap} \sinh \alpha} \gamma_0
+
\lr{ \lr{ \Bx \cdot \vcap} \cosh \alpha -x^0 \sinh \alpha } \vcap \gamma_0
+
\lr{ \Bx \wedge \vcap} \vcap \gamma_0 \\
&=
\begin{bmatrix}
\gamma_0 & \vcap \gamma_0
\end{bmatrix}
\begin{bmatrix}
\cosh\alpha & – \sinh\alpha \\
-\sinh\alpha & \cosh\alpha
\end{bmatrix}
\begin{bmatrix}
x^0 \\
\Bx \cdot \vcap
\end{bmatrix}
+
\lr{ \Bx \wedge \vcap} \vcap \gamma_0,
\end{aligned}
\end{equation}
which has the desired Lorentz boost structure. Of course, this is usually seen with \( \vcap = \gamma_{10} \) so that the components in the coordinate column vector are \( (ct, x) \).

End proof.

Theorem 1.3: Spatial rotation.

Given two linearly independent spatial bivectors \( \Ba = a^k \gamma_{k0}, \Bb = b^k \gamma_{k0} \), a rotation of \(\theta\) radians in the plane of \( \Ba, \Bb \) from \( \Ba \) towards \( \Bb \), is given by
\begin{equation}\label{eqn:lorentzTransform:640}
x’ = e^{-i\theta} x e^{i\theta},
\end{equation}
where \( i = (\Ba \wedge \Bb)/\Abs{\Ba \wedge \Bb} \), is a unit (spatial) bivector.

Start proof:

Without loss of generality, we may pick \( i = \acap \bcap \), where \( \acap^2 = \bcap^2 = 1 \), and \( \acap \cdot \bcap = 0 \). With such an orthonormal basis for the plane, we can decompose our four vector into portions that lie in and off the plane
\begin{equation}\label{eqn:lorentzTransform:400}
\begin{aligned}
x
&= \lr{ x^0 + \Bx } \gamma_0 \\
&= \lr{ x^0 + \Bx i i^{-1} } \gamma_0 \\
&= \lr{ x^0 + \lr{ \Bx \cdot i } i^{-1} + \lr{ \Bx \wedge i } i^{-1} } \gamma_0.
\end{aligned}
\end{equation}
The projective term lies in the plane of rotation, whereas the timelike and spatial rejection term are perpendicular. That is
\begin{equation}\label{eqn:lorentzTransform:420}
\begin{aligned}
x_\parallel &= \lr{ \Bx \cdot i } i^{-1} \gamma_0 \\
x_\perp &= \lr{ x^0 + \lr{ \Bx \wedge i } i^{-1} } \gamma_0,
\end{aligned}
\end{equation}
where \( x_\parallel \wedge i = 0 \), and \( x_\perp \cdot i = 0 \). The plane pseudoscalar \( i \) anticommutes with \( x_\parallel \), and commutes with \( x_\perp \), so
\begin{equation}\label{eqn:lorentzTransform:440}
\begin{aligned}
x’
&= e^{-i\theta/2} \lr{ x_\parallel + x_\perp } e^{i\theta/2} \\
&= x_\parallel e^{i\theta} + x_\perp.
\end{aligned}
\end{equation}
However
\begin{equation}\label{eqn:lorentzTransform:460}
\begin{aligned}
\lr{ \Bx \cdot i } i^{-1}
&=
\lr{ \Bx \cdot \lr{ \acap \wedge \bcap } } \bcap \acap \\
&=
\lr{\Bx \cdot \acap} \bcap \bcap \acap
-\lr{\Bx \cdot \bcap} \acap \bcap \acap \\
&=
\lr{\Bx \cdot \acap} \acap
+\lr{\Bx \cdot \bcap} \bcap,
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:lorentzTransform:480}
\begin{aligned}
x_\parallel e^{i\theta}
&=
\lr{
\lr{\Bx \cdot \acap} \acap
+
\lr{\Bx \cdot \bcap} \bcap
}
\gamma_0
\lr{
\cos\theta + \acap \bcap \sin\theta
} \\
&=
\acap \lr{
\lr{\Bx \cdot \acap} \cos\theta
–
\lr{\Bx \cdot \bcap} \sin\theta
}
\gamma_0
+
\bcap \lr{
\lr{\Bx \cdot \acap} \sin\theta
+
\lr{\Bx \cdot \bcap} \cos\theta
}
\gamma_0,
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:lorentzTransform:500}
x’
=
\begin{bmatrix}
\acap & \bcap
\end{bmatrix}
\begin{bmatrix}
\cos\theta & – \sin\theta \\
\sin\theta & \cos\theta
\end{bmatrix}
\begin{bmatrix}
\Bx \cdot \acap \\
\Bx \cdot \bcap \\
\end{bmatrix}
\gamma_0
+
\lr{ x \wedge i} i^{-1} \gamma_0.
\end{equation}
Observe that this rejection term can be explicitly expanded to
\begin{equation}\label{eqn:lorentzTransform:520}
\lr{ \Bx \wedge i} i^{-1} \gamma_0 =
x –
\lr{ \Bx \cdot \acap } \acap \gamma_0
–
\lr{ \Bx \cdot \acap } \acap \gamma_0.
\end{equation}
This is the timelike component of the vector, plus the spatial component that is normal to the plane. This exponential sandwich transformation rotates only the portion of the vector that lies in the plane, and leaves the rest (timelike and normal) untouched.

End proof.

Problems.

Problem: Verify components relative to boost direction.

In the proof of thm. 1.2, the vector \( x \) was expanded in terms of the spacetime split. An alternate approach, is to expand as
\begin{equation}\label{eqn:lorentzTransform:340}
\begin{aligned}
x
&= x \vcap^2 \\
&= \lr{ x \cdot \vcap + x \wedge \vcap } \vcap \\
&= \lr{ x \cdot \vcap } \vcap + \lr{ x \wedge \vcap } \vcap.
\end{aligned}
\end{equation}
Show that
\begin{equation}\label{eqn:lorentzTransform:360}
\lr{ x \cdot \vcap } \vcap
=
\lr{ x^0 + \lr{ \Bx \cdot \vcap} \vcap } \gamma_0,
\end{equation}
and
\begin{equation}\label{eqn:lorentzTransform:380}
\lr{ x \wedge \vcap } \vcap
=
\lr{ \Bx \wedge \vcap} \vcap \gamma_0.
\end{equation}

Answer

Let \( x = x^\mu \gamma_\mu \), so that
\begin{equation}\label{eqn:lorentzTransform:160}
\begin{aligned}
x \cdot \vcap
&=
\gpgradeone{ x^\mu \gamma_\mu \cos\theta^b \gamma_{b 0} } \\
&=
x^\mu \cos\theta^b \gpgradeone{ \gamma_\mu \gamma_{b 0} }
.
\end{aligned}
\end{equation}
The \( \mu = 0 \) component of this grade selection is
\begin{equation}\label{eqn:lorentzTransform:180}
\gpgradeone{ \gamma_0 \gamma_{b 0} }
=
-\gamma_b,
\end{equation}
and for \( \mu = a \ne 0 \), we have
\begin{equation}\label{eqn:lorentzTransform:200}
\gpgradeone{ \gamma_a \gamma_{b 0} }
=
-\delta_{a b} \gamma_0,
\end{equation}
so we have
\begin{equation}\label{eqn:lorentzTransform:220}
\begin{aligned}
x \cdot \vcap
&=
x^0 \cos\theta^b (-\gamma_b)
+
x^a \cos\theta^b (-\delta_{ab} \gamma_0 ) \\
&=
-x^0 \vcap \gamma_0
–
x^b \cos\theta^b \gamma_0 \\
&=
– \lr{ x^0 \vcap + \Bx \cdot \vcap } \gamma_0,
\end{aligned}
\end{equation}
where \( \Bx = x \wedge \gamma_0 \) is the spatial portion of the four vector \( x \) relative to the stationary observer frame. Since \( \vcap \) anticommutes with \( \gamma_0 \), the component of \( x \) in the spacetime plane \( \vcap \) is
\begin{equation}\label{eqn:lorentzTransform:240}
\lr{ x \cdot \vcap } \vcap =
\lr{ x^0 + \lr{ \Bx \cdot \vcap} \vcap } \gamma_0,
\end{equation}
as expected.

For the rejection term, we have
\begin{equation}\label{eqn:lorentzTransform:280}
x \wedge \vcap
=
x^\mu \cos\theta^s \gpgradethree{ \gamma_\mu \gamma_{s 0} }.
\end{equation}
The \( \mu = 0 \) term clearly contributes nothing, leaving us with:
\begin{equation}\label{eqn:lorentzTransform:300}
\begin{aligned}
\lr{ x \wedge \vcap } \vcap
&=
\lr{ x \wedge \vcap } \cdot \vcap \\
&=
x^r \cos\theta^s \cos\theta^t \lr{ \lr{ \gamma_r \wedge \gamma_{s}} \gamma_0 } \cdot \lr{ \gamma_{t0} } \\
&=
x^r \cos\theta^s \cos\theta^t \gpgradeone{
\lr{ \gamma_r \wedge \gamma_{s} } \gamma_0 \gamma_{t0}
} \\
&=
-x^r \cos\theta^s \cos\theta^t \lr{ \gamma_r \wedge \gamma_{s}} \cdot \gamma_t \\
&=
-x^r \cos\theta^s \cos\theta^t \lr{ -\gamma_r \delta_{st} + \gamma_s \delta_{rt} } \\
&=
x^r \cos\theta^t \cos\theta^t \gamma_r
–
x^t \cos\theta^s \cos\theta^t \gamma_s \\
&=
\Bx \gamma_0
– (\Bx \cdot \vcap) \vcap \gamma_0 \\
&=
\lr{ \Bx \wedge \vcap} \vcap \gamma_0,
\end{aligned}
\end{equation}
as expected. Is there a clever way to demonstrate this without resorting to coordinates?

Problem: Rotation transformation components.

Given a unit spatial bivector \( i = \acap \bcap \), where \( \acap \cdot \bcap = 0 \) and \( i^2 = -1 \), show that
\begin{equation}\label{eqn:lorentzTransform:540}
\lr{ x \cdot i } i^{-1}
=
\lr{ \Bx \cdot i } i^{-1} \gamma_0
=
\lr{\Bx \cdot \acap } \acap \gamma_0
+
\lr{\Bx \cdot \bcap } \bcap \gamma_0,
\end{equation}
and
\begin{equation}\label{eqn:lorentzTransform:560}
\lr{ x \wedge i } i^{-1}
=
\lr{ \Bx \wedge i } i^{-1} \gamma_0
=
x –
\lr{\Bx \cdot \acap } \acap \gamma_0
–
\lr{\Bx \cdot \bcap } \bcap \gamma_0.
\end{equation}
Also show that \( i \) anticommutes with \( \lr{ x \cdot i } i^{-1} \) and commutes with \( \lr{ x \wedge i } i^{-1} \).

Answer

This problem is left for the reader, as I don’t feel like typing out my solution.

The first part of this problem can be done in the tedious coordinate approach used above, but hopefully there is a better way.

For the last (commutation) part of the problem, here is a hint. Let \( x \wedge i = n i \), where \( n \cdot i = 0 \). The result then follows easily.

Geometric algebra notes collection split into two volumes

November 10, 2015 math and physics play , , , , , , , , , , , , ,

I’ve now split my (way too big) Exploring physics with Geometric Algebra into two volumes:

Each of these is now a much more manageable size, which should facilitate removing the redundancies in these notes, and making them more properly book like.

Also note I’ve also previously moved “Exploring Geometric Algebra” content related to:

  • Lagrangian’s
  • Hamiltonian’s
  • Noether’s theorem

into my classical mechanics collection (449 pages).