spacetime plane

Relativistic multivector surface integrals

December 31, 2020 math and physics play , , , , , , ,

[Click here for a PDF of this post]

Background.

This post is a continuation of:

Surface integrals.

[If mathjax doesn’t display properly for you, click here for a PDF of this post]

We’ve now covered line integrals and the fundamental theorem for line integrals, so it’s now time to move on to surface integrals.

Definition 1.1: Surface integral.

Given a two variable parameterization \( x = x(u,v) \), we write \( d^2\Bx = \Bx_u \wedge \Bx_v du dv \), and call
\begin{equation*}
\int F d^2\Bx\, G,
\end{equation*}
a surface integral, where \( F,G \) are arbitrary multivector functions.

Like our multivector line integral, this is intrinsically multivector valued, with a product of \( F \) with arbitrary grades, a bivector \( d^2 \Bx \), and \( G \), also potentially with arbitrary grades. Let’s consider an example.

Problem: Surface area integral example.

Given the hyperbolic surface parameterization \( x(\rho,\alpha) = \rho \gamma_0 e^{-\vcap \alpha} \), where \( \vcap = \gamma_{20} \) evaluate the indefinite integral
\begin{equation}\label{eqn:relativisticSurface:40}
\int \gamma_1 e^{\gamma_{21}\alpha} d^2 \Bx\, \gamma_2.
\end{equation}

Answer

We have \( \Bx_\rho = \gamma_0 e^{-\vcap \alpha} \) and \( \Bx_\alpha = \rho\gamma_{2} e^{-\vcap \alpha} \), so
\begin{equation}\label{eqn:relativisticSurface:60}
\begin{aligned}
d^2 \Bx
&=
(\Bx_\rho \wedge \Bx_\alpha) d\rho d\alpha \\
&=
\gpgradetwo{
\gamma_{0} e^{-\vcap \alpha} \rho\gamma_{2} e^{-\vcap \alpha}
}
d\rho d\alpha \\
&=
\rho \gamma_{02} d\rho d\alpha,
\end{aligned}
\end{equation}
so the integral is
\begin{equation}\label{eqn:relativisticSurface:80}
\begin{aligned}
\int \rho \gamma_1 e^{\gamma_{21}\alpha} \gamma_{022} d\rho d\alpha
&=
-\inv{2} \rho^2 \int \gamma_1 e^{\gamma_{21}\alpha} \gamma_{0} d\alpha \\
&=
\frac{\gamma_{01}}{2} \rho^2 \int e^{\gamma_{21}\alpha} d\alpha \\
&=
\frac{\gamma_{01}}{2} \rho^2 \gamma^{12} e^{\gamma_{21}\alpha} \\
&=
\frac{\rho^2 \gamma_{20}}{2} e^{\gamma_{21}\alpha}.
\end{aligned}
\end{equation}
Because \( F \) and \( G \) were both vectors, the resulting integral could only have been a multivector with grades 0,2,4. As it happens, there were no scalar nor pseudoscalar grades in the end result, and we ended up with the spacetime plane between \( \gamma_0 \), and \( \gamma_2 e^{\gamma_{21}\alpha} \), which are rotations of \(\gamma_2\) in the x,y plane. This is illustrated in fig. 1 (omitting scale and sign factors.)

fig. 1. Spacetime plane.

Fundamental theorem for surfaces.

For line integrals we saw that \( d\Bx \cdot \grad = \gpgradezero{ d\Bx \partial } \), and obtained the fundamental theorem for multivector line integrals by omitting the grade selection and using the multivector operator \( d\Bx \partial \) in the integrand directly. We have the same situation for surface integrals. In particular, we know that the \(\mathbb{R}^3\) Stokes theorem can be expressed in terms of \( d^2 \Bx \cdot \spacegrad \)

Problem: GA form of 3D Stokes’ theorem integrand.

Given an \(\mathbb{R}^3\) vector field \( \Bf \), show that
\begin{equation}\label{eqn:relativisticSurface:180}
\int dA \ncap \cdot \lr{ \spacegrad \cross \Bf }
=
-\int \lr{d^2\Bx \cdot \spacegrad } \cdot \Bf.
\end{equation}

Answer

Let \( d^2 \Bx = I \ncap dA \), implicitly fixing the relative orientation of the bivector area element compared to the chosen surface normal direction.
\begin{equation}\label{eqn:relativisticSurface:200}
\begin{aligned}
\int \lr{d^2\Bx \cdot \spacegrad } \cdot \Bf
&=
\int dA \gpgradeone{I \ncap \spacegrad } \cdot \Bf \\
&=
\int dA \lr{ I \lr{ \ncap \wedge \spacegrad} } \cdot \Bf \\
&=
\int dA \gpgradezero{ I^2 \lr{ \ncap \cross \spacegrad} \Bf } \\
&=
-\int dA \lr{ \ncap \cross \spacegrad} \cdot \Bf \\
&=
-\int dA \ncap \cdot \lr{ \spacegrad \cross \Bf }.
\end{aligned}
\end{equation}

The moral of the story is that the conventional dual form of the \(\mathbb{R}^3\) Stokes’ theorem can be written directly by projecting the gradient onto the surface area element. Geometrically, this projection operation has a rotational effect as well, since for bivector \( B \), and vector \( x \), the bivector-vector dot product \( B \cdot x \) is the component of \( x \) that lies in the plane \( B \wedge x = 0 \), but also rotated 90 degrees.

For multivector integration, we do not want an integral operator that includes such dot products. In the line integral case, we were able to achieve the same projective operation by using vector derivative instead of a dot product, and can do the same for the surface integral case. In particular

Theorem 1.1: Projection of gradient onto the tangent space.

Given a curvilinear representation of the gradient with respect to parameters \( u^0, u^1, u^2, u^3 \)
\begin{equation*}
\grad = \sum_\mu \Bx^\mu \PD{u^\mu}{},
\end{equation*}
the surface projection onto the tangent space associated with any two of those parameters, satisfies
\begin{equation*}
d^2 \Bx \cdot \grad = \gpgradeone{ d^2 \Bx \partial }.
\end{equation*}

Start proof:

Without loss of generality, we may pick \( u^0, u^1 \) as the parameters associated with the tangent space. The area element for the surface is
\begin{equation}\label{eqn:relativisticSurface:100}
d^2 \Bx = \Bx_0 \wedge \Bx_1 \,
du^0 du^1.
\end{equation}
Dotting this with the gradient gives
\begin{equation}\label{eqn:relativisticSurface:120}
\begin{aligned}
d^2 \Bx \cdot \grad
&=
du^0 du^1
\lr{ \Bx_0 \wedge \Bx_1 } \cdot \Bx^\mu \PD{u^\mu}{} \\
&=
du^0 du^1
\lr{
\Bx_0
\lr{\Bx_1 \cdot \Bx^\mu }
–
\Bx_1
\lr{\Bx_0 \cdot \Bx^\mu }
}
\PD{u^\mu}{} \\
&=
du^0 du^1
\lr{
\Bx_0 \PD{u^1}{}
–
\Bx_0 \PD{u^1}{}
}.
\end{aligned}
\end{equation}
On the other hand, the vector derivative for this surface is
\begin{equation}\label{eqn:relativisticSurface:140}
\partial
=
\Bx^0 \PD{u^0}{}
+
\Bx^1 \PD{u^1}{},
\end{equation}
so
\begin{equation}\label{eqn:relativisticSurface:160}
\begin{aligned}
\gpgradeone{d^2 \Bx \partial}
&=
du^0 du^1\,
\lr{ \Bx_0 \wedge \Bx_1 } \cdot
\lr{
\Bx^0 \PD{u^0}{}
+
\Bx^1 \PD{u^1}{}
} \\
&=
du^0 du^1
\lr{
\Bx_0 \PD{u^1}{}
–
\Bx_1 \PD{u^0}{}
}.
\end{aligned}
\end{equation}

End proof.

We now want to formulate the geometric algebra form of the fundamental theorem for surface integrals.

Theorem 1.2: Fundamental theorem for surface integrals.

Given multivector functions \( F, G \), and surface area element \( d^2 \Bx = \lr{ \Bx_u \wedge \Bx_v }\, du dv \), associated with a two parameter curve \( x(u,v) \), then
\begin{equation*}
\int_S F d^2\Bx \lrpartial G = \int_{\partial S} F d^1\Bx G,
\end{equation*}
where \( S \) is the integration surface, and \( \partial S \) designates its boundary, and the line integral on the RHS is really short hand for
\begin{equation*}
\int
\evalbar{ \lr{ F (-d\Bx_v) G } }{\Delta u}
+
\int
\evalbar{ \lr{ F (d\Bx_u) G } }{\Delta v},
\end{equation*}
which is a line integral that traverses the boundary of the surface with the opposite orientation to the circulation of the area element.

Start proof:

The vector derivative for this surface is
\begin{equation}\label{eqn:relativisticSurface:220}
\partial =
\Bx^u \PD{u}{}
+
\Bx^v \PD{v}{},
\end{equation}
so
\begin{equation}\label{eqn:relativisticSurface:240}
F d^2\Bx \lrpartial G
=
\PD{u}{} \lr{ F d^2\Bx\, \Bx^u G }
+
\PD{v}{} \lr{ F d^2\Bx\, \Bx^v G },
\end{equation}
where \( d^2\Bx\, \Bx^u \) is held constant with respect to \( u \), and \( d^2\Bx\, \Bx^v \) is held constant with respect to \( v \) (since the partials of the vector derivative act on \( F, G \), but not on the area element, nor on the reciprocal vectors of \( \lrpartial \) itself.) Note that
\begin{equation}\label{eqn:relativisticSurface:260}
d^2\Bx \wedge \Bx^u
=
du dv\, \lr{ \Bx_u \wedge \Bx_v } \wedge \Bx^u = 0,
\end{equation}
since \( \Bx^u \in sectionpan \setlr{ \Bx_u\, \Bx_v } \), so
\begin{equation}\label{eqn:relativisticSurface:280}
\begin{aligned}
d^2\Bx\, \Bx^u
&=
d^2\Bx \cdot \Bx^u
+
d^2\Bx \wedge \Bx^u \\
&=
d^2\Bx \cdot \Bx^u \\
&=
du dv\, \lr{ \Bx_u \wedge \Bx_v } \cdot \Bx^u \\
&=
-du dv\, \Bx_v.
\end{aligned}
\end{equation}
Similarly
\begin{equation}\label{eqn:relativisticSurface:300}
\begin{aligned}
d^2\Bx\, \Bx^v
&=
d^2\Bx \cdot \Bx^v \\
&=
du dv\, \lr{ \Bx_u \wedge \Bx_v } \cdot \Bx^v \\
&=
du dv\, \Bx_u.
\end{aligned}
\end{equation}
This leaves us with
\begin{equation}\label{eqn:relativisticSurface:320}
F d^2\Bx \lrpartial G
=
-du dv\,
\PD{u}{} \lr{ F \Bx_v G }
+
du dv\,
\PD{v}{} \lr{ F \Bx_u G },
\end{equation}
where \( \Bx_v, \Bx_u \) are held constant with respect to \( u,v \) respectively. Fortuitously, this constant condition can be dropped, since the antisymmetry of the wedge in the area element results in perfect cancellation. If these line elements are not held constant then
\begin{equation}\label{eqn:relativisticSurface:340}
\PD{u}{} \lr{ F \Bx_v G }
–
\PD{v}{} \lr{ F \Bx_u G }
=
F \lr{
\PD{v}{\Bx_u}
–
\PD{u}{\Bx_v}
} G
+
\lr{
\PD{u}{F} \Bx_v G
+
F \Bx_v \PD{u}{G}
}
+
\lr{
\PD{v}{F} \Bx_u G
+
F \Bx_u \PD{v}{G}
}
,
\end{equation}
but the mixed partial contribution is zero
\begin{equation}\label{eqn:relativisticSurface:360}
\begin{aligned}
\PD{v}{\Bx_u}
–
\PD{u}{\Bx_v}
&=
\PD{v}{} \PD{u}{x}
–
\PD{u}{} \PD{v}{x} \\
&=
0,
\end{aligned}
\end{equation}
by equality of mixed partials. We have two perfect differentials, and can evaluate each of these integrals
\begin{equation}\label{eqn:relativisticSurface:380}
\begin{aligned}
\int F d^2\Bx \lrpartial G
&=
-\int
du dv\,
\PD{u}{} \lr{ F \Bx_v G }
+
\int
du dv\,
\PD{v}{} \lr{ F \Bx_u G } \\
&=
-\int
dv\,
\evalbar{ \lr{ F \Bx_v G } }{\Delta u}
+
\int
du\,
\evalbar{ \lr{ F \Bx_u G } }{\Delta v} \\
&=
\int
\evalbar{ \lr{ F (-d\Bx_v) G } }{\Delta u}
+
\int
\evalbar{ \lr{ F (d\Bx_u) G } }{\Delta v}.
\end{aligned}
\end{equation}
We use the shorthand \( d^1 \Bx = d\Bx_u – d\Bx_v \) to write
\begin{equation}\label{eqn:relativisticSurface:400}
\int_S F d^2\Bx \lrpartial G = \int_{\partial S} F d^1\Bx G,
\end{equation}
with the understanding that this is really instructions to evaluate the line integrals in the last step of \ref{eqn:relativisticSurface:380}.

End proof.

Problem: Integration in the t,y plane.

Let \( x(t,y) = c t \gamma_0 + y \gamma_2 \). Write out both sides of the fundamental theorem explicitly.

Answer

Let’s designate the tangent basis vectors as
\begin{equation}\label{eqn:relativisticSurface:420}
\Bx_0 = \PD{t}{x} = c \gamma_0,
\end{equation}
and
\begin{equation}\label{eqn:relativisticSurface:440}
\Bx_2 = \PD{y}{x} = \gamma_2,
\end{equation}
so the vector derivative is
\begin{equation}\label{eqn:relativisticSurface:460}
\partial
= \inv{c} \gamma^0 \PD{t}{}
+ \gamma^2 \PD{y}{},
\end{equation}
and the area element is
\begin{equation}\label{eqn:relativisticSurface:480}
d^2 \Bx = c \gamma_0 \gamma_2.
\end{equation}
The fundamental theorem of surface integrals is just a statement that
\begin{equation}\label{eqn:relativisticSurface:500}
\int_{t_0}^{t_1} c dt
\int_{y_0}^{y_1} dy
F \gamma_0 \gamma_2 \lr{
\inv{c} \gamma^0 \PD{t}{}
+ \gamma^2 \PD{y}{}
} G
=
\int F \lr{ c \gamma_0 dt – \gamma_2 dy } G,
\end{equation}
where the RHS, when stated explicitly, really means
\begin{equation}\label{eqn:relativisticSurface:520}
\begin{aligned}
\int &F \lr{ c \gamma_0 dt – \gamma_2 dy } G
=
\int_{t_0}^{t_1} c dt \lr{ F(t,y_1) \gamma_0 G(t, y_1) – F(t,y_0) \gamma_0 G(t, y_0) } \\
&\qquad –
\int_{y_0}^{y_1} dy \lr{ F(t_1,y) \gamma_2 G(t_1, y) – F(t_0,y) \gamma_0 G(t_0, y) }.
\end{aligned}
\end{equation}
In this particular case, since \( \Bx_0 = c \gamma_0, \Bx_2 = \gamma_2 \) are both constant functions that depend on neither \( t \) nor \( y \), it is easy to derive the full expansion of \ref{eqn:relativisticSurface:520} directly from the LHS of \ref{eqn:relativisticSurface:500}.

Problem: A cylindrical hyperbolic surface.

Generalizing the example surface integral from \ref{eqn:relativisticSurface:40}, let
\begin{equation}\label{eqn:relativisticSurface:540}
x(\rho, \alpha) = \rho e^{-\vcap \alpha/2} x(0,1) e^{\vcap \alpha/2},
\end{equation}
where \( \rho \) is a scalar, and \( \vcap = \cos\theta_k\gamma_{k0} \) is a unit spatial bivector, and \( \cos\theta_k \) are direction cosines of that vector. This is a composite transformation, where the \( \alpha \) variation boosts the \( x(0,1) \) four-vector, and the \( \rho \) parameter contracts or increases the magnitude of this vector, resulting in \( x \) spanning a hyperbolic region of spacetime.

Compute the tangent and reciprocal basis, the area element for the surface, and explicitly state both sides of the fundamental theorem.

Answer

For the tangent basis vectors we have
\begin{equation}\label{eqn:relativisticSurface:560}
\Bx_\rho = \PD{\rho}{x} =
e^{-\vcap \alpha/2} x(0,1) e^{\vcap \alpha/2} = \frac{x}{\rho},
\end{equation}
and
\begin{equation}\label{eqn:relativisticSurface:580}
\Bx_\alpha = \PD{\alpha}{x} =
\lr{-\vcap/2} x
+
x \lr{ \vcap/2 }
=
x \cdot \vcap.
\end{equation}
These vectors \( \Bx_\rho, \Bx_\alpha \) are orthogonal, as \( x \cdot \vcap \) is the projection of \( x \) onto the spacetime plane \( x \wedge \vcap = 0 \), but rotated so that \( x \cdot \lr{ x \cdot \vcap } = 0 \). Because of this orthogonality, the vector derivative for this tangent space is
\begin{equation}\label{eqn:relativisticSurface:600}
\partial =
\inv{x \cdot \vcap} \PD{\alpha}{}
+
\frac{\rho}{x}
\PD{\rho}{}
.
\end{equation}
The area element is
\begin{equation}\label{eqn:relativisticSurface:620}
\begin{aligned}
d^2 \Bx
&=
d\rho d\alpha\,
\frac{x}{\rho} \wedge \lr{ x \cdot \vcap } \\
&=
\inv{\rho} d\rho d\alpha\,
x \lr{ x \cdot \vcap }
.
\end{aligned}
\end{equation}
The full statement of the fundamental theorem for this surface is
\begin{equation}\label{eqn:relativisticSurface:640}
\int_S
d\rho d\alpha\,
F
\lr{
\inv{\rho} x \lr{ x \cdot \vcap }
}
\lr{
\inv{x \cdot \vcap} \PD{\alpha}{}
+
\frac{\rho}{x}
\PD{\rho}{}
}
G
=
\int_{\partial S}
F \lr{ d\rho \frac{x}{\rho} – d\alpha \lr{ x \cdot \vcap } } G.
\end{equation}
As in the previous example, due to the orthogonality of the tangent basis vectors, it’s easy to show find the RHS directly from the LHS.

Problem: Simple example with non-orthogonal tangent space basis vectors.

Let \( x(u,v) = u a + v b \), where \( u,v \) are scalar parameters, and \( a, b \) are non-null and non-colinear constant four-vectors. Write out the fundamental theorem for surfaces with respect to this parameterization.

Answer

The tangent basis vectors are just \( \Bx_u = a, \Bx_v = b \), with reciprocals
\begin{equation}\label{eqn:relativisticSurface:660}
\Bx^u = \Bx_v \cdot \inv{ \Bx_u \wedge \Bx_v } = b \cdot \inv{ a \wedge b },
\end{equation}
and
\begin{equation}\label{eqn:relativisticSurface:680}
\Bx^v = -\Bx_u \cdot \inv{ \Bx_u \wedge \Bx_v } = -a \cdot \inv{ a \wedge b }.
\end{equation}
The fundamental theorem, with respect to this surface, when written out explicitly takes the form
\begin{equation}\label{eqn:relativisticSurface:700}
\int F \, du dv\, \lr{ a \wedge b } \inv{ a \wedge b } \cdot \lr{ a \PD{u}{} – b \PD{v}{} } G
=
\int F \lr{ a du – b dv } G.
\end{equation}
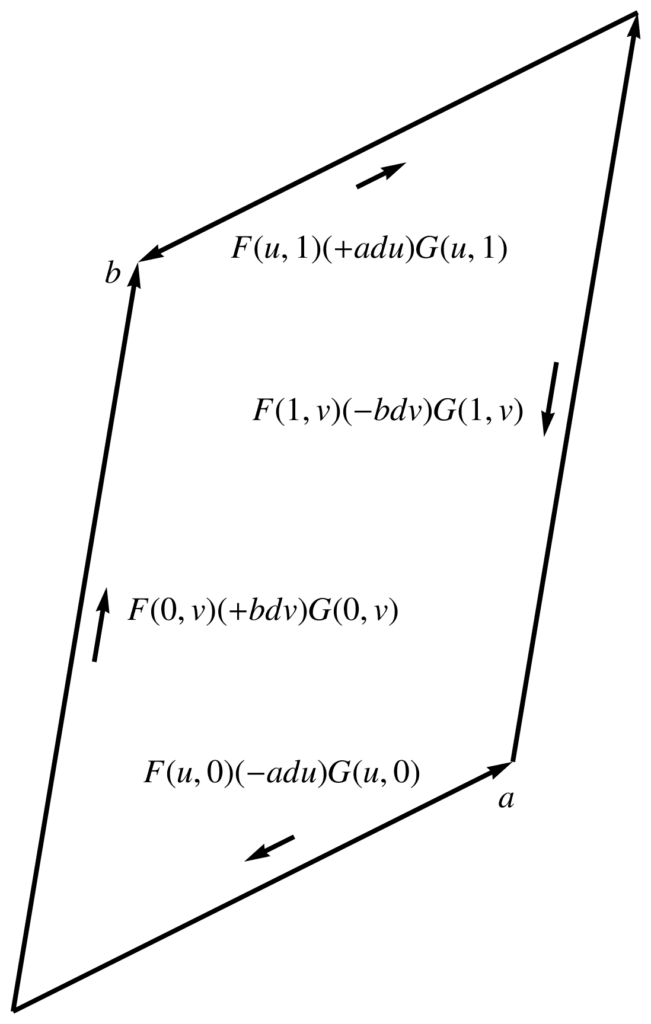
This is a good example to illustrate the geometry of the line integral circulation.
Suppose that we are integrating over \( u \in [0,1], v \in [0,1] \). In this case, the line integral really means
\begin{equation}\label{eqn:relativisticSurface:720}
\begin{aligned}
\int &F \lr{ a du – b dv } G
=
+
\int F(u,1) (+a du) G(u,1)
+
\int F(u,0) (-a du) G(u,0) \\
&\quad+
\int F(1,v) (-b dv) G(1,v)
+
\int F(0,v) (+b dv) G(0,v),
\end{aligned}
\end{equation}
which is a path around the spacetime parallelogram spanned by \( u, v \), as illustrated in fig. 1, which illustrates the orientation of the bivector area element with the arrows around the exterior of the parallelogram: \( 0 \rightarrow a \rightarrow a + b \rightarrow b \rightarrow 0 \).

fig. 2. Line integral orientation.

Lorentz transformations in Space Time Algebra (STA)

December 12, 2020 math and physics play , , , , , , , , , , , , , , , , , ,

[If mathjax doesn’t display properly for you, click here for a PDF of this post]

Motivation.

One of the remarkable features of geometric algebra are the complex exponential sandwiches that can be used to encode rotations in any dimension, or rotation like operations like Lorentz transformations in Minkowski spaces. In this post, we show some examples that unpack the geometric algebra expressions for Lorentz transformations operations of this sort. In particular, we will look at the exponential sandwich operations for spatial rotations and Lorentz boosts in the Dirac algebra, known as Space Time Algebra (STA) in geometric algebra circles, and demonstrate that these sandwiches do have the desired effects.

Lorentz transformations.

Theorem 1.1: Lorentz transformation.

The transformation
\begin{equation}\label{eqn:lorentzTransform:580}
x \rightarrow e^{B} x e^{-B} = x’,
\end{equation}
where \( B = a \wedge b \), is an STA 2-blade for any two linearly independent four-vectors \( a, b \), is a norm preserving, that is
\begin{equation}\label{eqn:lorentzTransform:600}
x^2 = {x’}^2.
\end{equation}

Start proof:

The proof is disturbingly trivial in this geometric algebra form
\begin{equation}\label{eqn:lorentzTransform:40}
\begin{aligned}
{x’}^2
&=
e^{B} x e^{-B} e^{B} x e^{-B} \\
&=
e^{B} x x e^{-B} \\
&=
x^2 e^{B} e^{-B} \\
&=
x^2.
\end{aligned}
\end{equation}

End proof.

In particular, observe that we did not need to construct the usual infinitesimal representations of rotation and boost transformation matrices or tensors in order to demonstrate that we have spacetime invariance for the transformations. The rough idea of such a transformation is that the exponential commutes with components of the four-vector that lie off the spacetime plane specified by the bivector \( B \), and anticommutes with components of the four-vector that lie in the plane. The end result is that the sandwich operation simplifies to
\begin{equation}\label{eqn:lorentzTransform:60}
x’ = x_\parallel e^{-B} + x_\perp,
\end{equation}
where \( x = x_\perp + x_\parallel \) and \( x_\perp \cdot B = 0 \), and \( x_\parallel \wedge B = 0 \). In particular, using \( x = x B B^{-1} = \lr{ x \cdot B + x \wedge B } B^{-1} \), we find that
\begin{equation}\label{eqn:lorentzTransform:80}
\begin{aligned}
x_\parallel &= \lr{ x \cdot B } B^{-1} \\
x_\perp &= \lr{ x \wedge B } B^{-1}.
\end{aligned}
\end{equation}
When \( B \) is a spacetime plane \( B = b \wedge \gamma_0 \), then this exponential has a hyperbolic nature, and we end up with a Lorentz boost. When \( B \) is a spatial bivector, we end up with a single complex exponential, encoding our plane old 3D rotation. More general \( B \)’s that encode composite boosts and rotations are also possible, but \( B \) must be invertible (it should have no lightlike factors.) The rough geometry of these projections is illustrated in fig 1, where the spacetime plane is represented by \( B \).

Projection and rejection geometry.

fig 1. Projection and rejection geometry.

 

What is not so obvious is how to pick \( B \)’s that correspond to specific rotation axes or boost directions. Let’s consider each of those cases in turn.

Theorem 1.2: Boost.

The boost along a direction vector \( \vcap \) and rapidity \( \alpha \) is given by
\begin{equation}\label{eqn:lorentzTransform:620}
x’ = e^{-\vcap \alpha/2} x e^{\vcap \alpha/2},
\end{equation}
where \( \vcap = \gamma_{k0} \cos\theta^k \) is an STA bivector representing a spatial direction with direction cosines \( \cos\theta^k \).

Start proof:

We want to demonstrate that this is equivalent to the usual boost formulation. We can start with decomposition of the four-vector \( x \) into components that lie in and off of the spacetime plane \( \vcap \).
\begin{equation}\label{eqn:lorentzTransform:100}
\begin{aligned}
x
&= \lr{ x^0 + \Bx } \gamma_0 \\
&= \lr{ x^0 + \Bx \vcap^2 } \gamma_0 \\
&= \lr{ x^0 + \lr{ \Bx \cdot \vcap} \vcap + \lr{ \Bx \wedge \vcap} \vcap } \gamma_0,
\end{aligned}
\end{equation}
where \( \Bx = x \wedge \gamma_0 \). The first two components lie in the boost plane, whereas the last is the spatial component of the vector that lies perpendicular to the boost plane. Observe that \( \vcap \) anticommutes with the dot product term and commutes with he wedge product term, so we have
\begin{equation}\label{eqn:lorentzTransform:120}
\begin{aligned}
x’
&=
\lr{ x^0 + \lr{ \Bx \cdot \vcap } \vcap } \gamma_0
e^{\vcap \alpha/2 }
e^{\vcap \alpha/2 }
+
\lr{ \Bx \wedge \vcap } \vcap \gamma_0
e^{-\vcap \alpha/2 }
e^{\vcap \alpha/2 } \\
&=
\lr{ x^0 + \lr{ \Bx \cdot \vcap } \vcap } \gamma_0
e^{\vcap \alpha }
+
\lr{ \Bx \wedge \vcap } \vcap \gamma_0.
\end{aligned}
\end{equation}
Noting that \( \vcap^2 = 1 \), we may expand the exponential in hyperbolic functions, and find that the boosted portion of the vector expands as
\begin{equation}\label{eqn:lorentzTransform:260}
\begin{aligned}
\lr{ x^0 + \lr{ \Bx \cdot \vcap} \vcap } \gamma_0 e^{\vcap \alpha}
&=
\lr{ x^0 + \lr{ \Bx \cdot \vcap} \vcap } \gamma_0 \lr{ \cosh\alpha + \vcap \sinh \alpha} \\
&=
\lr{ x^0 + \lr{ \Bx \cdot \vcap} \vcap } \lr{ \cosh\alpha – \vcap \sinh \alpha} \gamma_0 \\
&=
\lr{ x^0 \cosh\alpha – \lr{ \Bx \cdot \vcap} \sinh \alpha} \gamma_0
+
\lr{ -x^0 \sinh \alpha + \lr{ \Bx \cdot \vcap} \cosh \alpha } \vcap \gamma_0.
\end{aligned}
\end{equation}
We are left with
\begin{equation}\label{eqn:lorentzTransform:320}
\begin{aligned}
x’
&=
\lr{ x^0 \cosh\alpha – \lr{ \Bx \cdot \vcap} \sinh \alpha} \gamma_0
+
\lr{ \lr{ \Bx \cdot \vcap} \cosh \alpha -x^0 \sinh \alpha } \vcap \gamma_0
+
\lr{ \Bx \wedge \vcap} \vcap \gamma_0 \\
&=
\begin{bmatrix}
\gamma_0 & \vcap \gamma_0
\end{bmatrix}
\begin{bmatrix}
\cosh\alpha & – \sinh\alpha \\
-\sinh\alpha & \cosh\alpha
\end{bmatrix}
\begin{bmatrix}
x^0 \\
\Bx \cdot \vcap
\end{bmatrix}
+
\lr{ \Bx \wedge \vcap} \vcap \gamma_0,
\end{aligned}
\end{equation}
which has the desired Lorentz boost structure. Of course, this is usually seen with \( \vcap = \gamma_{10} \) so that the components in the coordinate column vector are \( (ct, x) \).

End proof.

Theorem 1.3: Spatial rotation.

Given two linearly independent spatial bivectors \( \Ba = a^k \gamma_{k0}, \Bb = b^k \gamma_{k0} \), a rotation of \(\theta\) radians in the plane of \( \Ba, \Bb \) from \( \Ba \) towards \( \Bb \), is given by
\begin{equation}\label{eqn:lorentzTransform:640}
x’ = e^{-i\theta} x e^{i\theta},
\end{equation}
where \( i = (\Ba \wedge \Bb)/\Abs{\Ba \wedge \Bb} \), is a unit (spatial) bivector.

Start proof:

Without loss of generality, we may pick \( i = \acap \bcap \), where \( \acap^2 = \bcap^2 = 1 \), and \( \acap \cdot \bcap = 0 \). With such an orthonormal basis for the plane, we can decompose our four vector into portions that lie in and off the plane
\begin{equation}\label{eqn:lorentzTransform:400}
\begin{aligned}
x
&= \lr{ x^0 + \Bx } \gamma_0 \\
&= \lr{ x^0 + \Bx i i^{-1} } \gamma_0 \\
&= \lr{ x^0 + \lr{ \Bx \cdot i } i^{-1} + \lr{ \Bx \wedge i } i^{-1} } \gamma_0.
\end{aligned}
\end{equation}
The projective term lies in the plane of rotation, whereas the timelike and spatial rejection term are perpendicular. That is
\begin{equation}\label{eqn:lorentzTransform:420}
\begin{aligned}
x_\parallel &= \lr{ \Bx \cdot i } i^{-1} \gamma_0 \\
x_\perp &= \lr{ x^0 + \lr{ \Bx \wedge i } i^{-1} } \gamma_0,
\end{aligned}
\end{equation}
where \( x_\parallel \wedge i = 0 \), and \( x_\perp \cdot i = 0 \). The plane pseudoscalar \( i \) anticommutes with \( x_\parallel \), and commutes with \( x_\perp \), so
\begin{equation}\label{eqn:lorentzTransform:440}
\begin{aligned}
x’
&= e^{-i\theta/2} \lr{ x_\parallel + x_\perp } e^{i\theta/2} \\
&= x_\parallel e^{i\theta} + x_\perp.
\end{aligned}
\end{equation}
However
\begin{equation}\label{eqn:lorentzTransform:460}
\begin{aligned}
\lr{ \Bx \cdot i } i^{-1}
&=
\lr{ \Bx \cdot \lr{ \acap \wedge \bcap } } \bcap \acap \\
&=
\lr{\Bx \cdot \acap} \bcap \bcap \acap
-\lr{\Bx \cdot \bcap} \acap \bcap \acap \\
&=
\lr{\Bx \cdot \acap} \acap
+\lr{\Bx \cdot \bcap} \bcap,
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:lorentzTransform:480}
\begin{aligned}
x_\parallel e^{i\theta}
&=
\lr{
\lr{\Bx \cdot \acap} \acap
+
\lr{\Bx \cdot \bcap} \bcap
}
\gamma_0
\lr{
\cos\theta + \acap \bcap \sin\theta
} \\
&=
\acap \lr{
\lr{\Bx \cdot \acap} \cos\theta
–
\lr{\Bx \cdot \bcap} \sin\theta
}
\gamma_0
+
\bcap \lr{
\lr{\Bx \cdot \acap} \sin\theta
+
\lr{\Bx \cdot \bcap} \cos\theta
}
\gamma_0,
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:lorentzTransform:500}
x’
=
\begin{bmatrix}
\acap & \bcap
\end{bmatrix}
\begin{bmatrix}
\cos\theta & – \sin\theta \\
\sin\theta & \cos\theta
\end{bmatrix}
\begin{bmatrix}
\Bx \cdot \acap \\
\Bx \cdot \bcap \\
\end{bmatrix}
\gamma_0
+
\lr{ x \wedge i} i^{-1} \gamma_0.
\end{equation}
Observe that this rejection term can be explicitly expanded to
\begin{equation}\label{eqn:lorentzTransform:520}
\lr{ \Bx \wedge i} i^{-1} \gamma_0 =
x –
\lr{ \Bx \cdot \acap } \acap \gamma_0
–
\lr{ \Bx \cdot \acap } \acap \gamma_0.
\end{equation}
This is the timelike component of the vector, plus the spatial component that is normal to the plane. This exponential sandwich transformation rotates only the portion of the vector that lies in the plane, and leaves the rest (timelike and normal) untouched.

End proof.

Problems.

Problem: Verify components relative to boost direction.

In the proof of thm. 1.2, the vector \( x \) was expanded in terms of the spacetime split. An alternate approach, is to expand as
\begin{equation}\label{eqn:lorentzTransform:340}
\begin{aligned}
x
&= x \vcap^2 \\
&= \lr{ x \cdot \vcap + x \wedge \vcap } \vcap \\
&= \lr{ x \cdot \vcap } \vcap + \lr{ x \wedge \vcap } \vcap.
\end{aligned}
\end{equation}
Show that
\begin{equation}\label{eqn:lorentzTransform:360}
\lr{ x \cdot \vcap } \vcap
=
\lr{ x^0 + \lr{ \Bx \cdot \vcap} \vcap } \gamma_0,
\end{equation}
and
\begin{equation}\label{eqn:lorentzTransform:380}
\lr{ x \wedge \vcap } \vcap
=
\lr{ \Bx \wedge \vcap} \vcap \gamma_0.
\end{equation}

Answer

Let \( x = x^\mu \gamma_\mu \), so that
\begin{equation}\label{eqn:lorentzTransform:160}
\begin{aligned}
x \cdot \vcap
&=
\gpgradeone{ x^\mu \gamma_\mu \cos\theta^b \gamma_{b 0} } \\
&=
x^\mu \cos\theta^b \gpgradeone{ \gamma_\mu \gamma_{b 0} }
.
\end{aligned}
\end{equation}
The \( \mu = 0 \) component of this grade selection is
\begin{equation}\label{eqn:lorentzTransform:180}
\gpgradeone{ \gamma_0 \gamma_{b 0} }
=
-\gamma_b,
\end{equation}
and for \( \mu = a \ne 0 \), we have
\begin{equation}\label{eqn:lorentzTransform:200}
\gpgradeone{ \gamma_a \gamma_{b 0} }
=
-\delta_{a b} \gamma_0,
\end{equation}
so we have
\begin{equation}\label{eqn:lorentzTransform:220}
\begin{aligned}
x \cdot \vcap
&=
x^0 \cos\theta^b (-\gamma_b)
+
x^a \cos\theta^b (-\delta_{ab} \gamma_0 ) \\
&=
-x^0 \vcap \gamma_0
–
x^b \cos\theta^b \gamma_0 \\
&=
– \lr{ x^0 \vcap + \Bx \cdot \vcap } \gamma_0,
\end{aligned}
\end{equation}
where \( \Bx = x \wedge \gamma_0 \) is the spatial portion of the four vector \( x \) relative to the stationary observer frame. Since \( \vcap \) anticommutes with \( \gamma_0 \), the component of \( x \) in the spacetime plane \( \vcap \) is
\begin{equation}\label{eqn:lorentzTransform:240}
\lr{ x \cdot \vcap } \vcap =
\lr{ x^0 + \lr{ \Bx \cdot \vcap} \vcap } \gamma_0,
\end{equation}
as expected.

For the rejection term, we have
\begin{equation}\label{eqn:lorentzTransform:280}
x \wedge \vcap
=
x^\mu \cos\theta^s \gpgradethree{ \gamma_\mu \gamma_{s 0} }.
\end{equation}
The \( \mu = 0 \) term clearly contributes nothing, leaving us with:
\begin{equation}\label{eqn:lorentzTransform:300}
\begin{aligned}
\lr{ x \wedge \vcap } \vcap
&=
\lr{ x \wedge \vcap } \cdot \vcap \\
&=
x^r \cos\theta^s \cos\theta^t \lr{ \lr{ \gamma_r \wedge \gamma_{s}} \gamma_0 } \cdot \lr{ \gamma_{t0} } \\
&=
x^r \cos\theta^s \cos\theta^t \gpgradeone{
\lr{ \gamma_r \wedge \gamma_{s} } \gamma_0 \gamma_{t0}
} \\
&=
-x^r \cos\theta^s \cos\theta^t \lr{ \gamma_r \wedge \gamma_{s}} \cdot \gamma_t \\
&=
-x^r \cos\theta^s \cos\theta^t \lr{ -\gamma_r \delta_{st} + \gamma_s \delta_{rt} } \\
&=
x^r \cos\theta^t \cos\theta^t \gamma_r
–
x^t \cos\theta^s \cos\theta^t \gamma_s \\
&=
\Bx \gamma_0
– (\Bx \cdot \vcap) \vcap \gamma_0 \\
&=
\lr{ \Bx \wedge \vcap} \vcap \gamma_0,
\end{aligned}
\end{equation}
as expected. Is there a clever way to demonstrate this without resorting to coordinates?

Problem: Rotation transformation components.

Given a unit spatial bivector \( i = \acap \bcap \), where \( \acap \cdot \bcap = 0 \) and \( i^2 = -1 \), show that
\begin{equation}\label{eqn:lorentzTransform:540}
\lr{ x \cdot i } i^{-1}
=
\lr{ \Bx \cdot i } i^{-1} \gamma_0
=
\lr{\Bx \cdot \acap } \acap \gamma_0
+
\lr{\Bx \cdot \bcap } \bcap \gamma_0,
\end{equation}
and
\begin{equation}\label{eqn:lorentzTransform:560}
\lr{ x \wedge i } i^{-1}
=
\lr{ \Bx \wedge i } i^{-1} \gamma_0
=
x –
\lr{\Bx \cdot \acap } \acap \gamma_0
–
\lr{\Bx \cdot \bcap } \bcap \gamma_0.
\end{equation}
Also show that \( i \) anticommutes with \( \lr{ x \cdot i } i^{-1} \) and commutes with \( \lr{ x \wedge i } i^{-1} \).

Answer

This problem is left for the reader, as I don’t feel like typing out my solution.

The first part of this problem can be done in the tedious coordinate approach used above, but hopefully there is a better way.

For the last (commutation) part of the problem, here is a hint. Let \( x \wedge i = n i \), where \( n \cdot i = 0 \). The result then follows easily.