[Click here for a PDF version of this post]

Here’s another real integral problem from [1] (31(f)). Find
\begin{equation}\label{eqn:weightedSinc:20}
I = \int_0^\infty \frac{\sin x dx}{x\lr{ x^2 + a^2 }}.
\end{equation}
Both Mathematica and the text state that the answer is
\begin{equation}\label{eqn:weightedSinc:40}
I = \frac{\pi}{2 a^2} \lr{ 1 – e^{-a}}.
\end{equation}

My initial attempt to evaluate this using contour integral techniques gets the wrong answer. I’m going to post both my wrong solution method, and why the initial method was wrong.

Then I’ll follow up with the corrected method. The mistake, and it’s identification, is probably more interesting than the solution.

The contour.

Before delving into the residue calculations, it’s first helpful to note that the integrand is an even function, so we may transform it first into an integral over the entire real axis:
\begin{equation}\label{eqn:weightedSinc:60}
I = \inv{2} \int_{-\infty}^\infty \frac{\sin x dx}{x\lr{ x^2 + a^2 }}.
\end{equation}
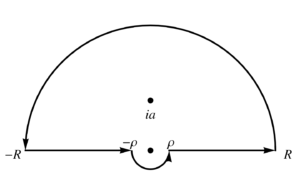
The obvious choice for the contour is illustrated in fig. 1, where \( R \rightarrow \infty \), and \( \rho \rightarrow 0 \).

fig. 1. Contour with two semicircles.

We have to figure out if the circular contour integrals are zero, in the limit. Let’s start with the small contour, with \( z = \rho e^{i \theta} \)
\begin{equation}\label{eqn:weightedSinc:80}
\begin{aligned}
I_\rho
&= \inv{2} \oint \frac{\sin z dz}{z \lr{ z^2 + a^2 }} \\
&= \inv{2} \int_\pi^{2 \pi} \frac{\sin\lr{ \rho e^{i\theta} } \rho i e^{i \theta} d\theta}{\rho e^{i\theta} \lr{ \rho^2 e^{2 i \theta} + a^2 }} \\
&\approx \inv{2} \int_\pi^{2 \pi} \frac{\rho e^{i\theta} d\theta}{\lr{ \rho^2 e^{2 i \theta} + a^2 }} \\
&= \frac{\rho}{2} \int_\pi^{2 \pi} \frac{e^{i\theta} d\theta}{\lr{ \rho^2 e^{2 i \theta} + a^2 }} \\
&\rightarrow \frac{\rho}{2 a^2} \int_\pi^{2 \pi} e^{i\theta} d\theta \\
&\rightarrow 0.
\end{aligned}
\end{equation}

The wrong way.

To complete the problem, I did a similar argument showing that the limit along the infinite semicircle was zero, and then proceeded to evaluate the residues. Let’s see what we get if this is done. We are trying to evaluate

\begin{equation}\label{eqn:weightedSinc:100}
I = \inv{2} \oint \frac{\sin z dz}{z \lr{ z + ia } \lr{ z – ia } },
\end{equation}
where we have a “half-enclosed” pole at \( z = 0 \), and fully enclosed pole at \( z = i a \). The residues are

\begin{equation}\label{eqn:weightedSinc:120}
\begin{aligned}
I
&= \inv{2} \lr{ 2 \pi i } \lr{ \evalbar{ \frac{\sin z}{z \lr{ z + ia } } }{z = i a} + \evalbar{ \inv{2} \frac{\sin z}{\lr{ z^2 + a^2 }} }{z = 0} } \\
&= \inv{2} \lr{ 2 \pi i } \frac{e^{i^2 a} – e^{-i^2 a}}{2i \lr{ ia } \lr{ 2 ia } } \\
&= \frac{ \pi }{4 a^2} \lr{e^{a} – e^{-a}}.
\end{aligned}
\end{equation}

This has a similar structure to the actual answer, but is wrong. I couldn’t find any obvious mistake in the residue calculation, so I was scratching my head for a while about what I did wrong. This confusion was only compounded by figuring out a different way to evaluate this, which did yield the right answer.

The right way.

The key to getting the right answer is to notice that
\begin{equation}\label{eqn:weightedSinc:65}
\inv{2} \int_{-\infty}^\infty \frac{\cos x dx}{x\lr{ x^2 + a^2 }} = 0,
\end{equation}
so we can, instead compute
\begin{equation}\label{eqn:weightedSinc:70}
I = \inv{2} \textrm{Im} \int_{-\infty}^\infty \frac{e^{ix} dx}{x\lr{ x^2 + a^2 }}.
\end{equation}
It’s easy to repeat the argument that after the \( x \rightarrow z \) substitution, this is also zero on the small semicircle, in the \( \rho \rightarrow 0 \) limit. On the large semicircle, the integrand is now in the perfect form to apply Jordan’s lemma. Recall that lemma was:

Lemma 1.1: Jordan’s Lemma.

We have \( \alpha = 1 \), which is greater than zero, and the rest of the integrand is \( O(R^{-3}) \), so it’s zero. Now we can just compute the residues

\begin{equation}\label{eqn:weightedSinc:140}
\begin{aligned}
\inv{2} \oint \frac{e^{iz} dz}{z\lr{ z^2 + a^2 }}
&=
\lr{ \pi i } \lr{ \evalbar{ \frac{e^{iz}}{z \lr{ z + i a }} }{z = i a} + \inv{2} \evalbar{ \frac{e^{iz}}{z^2 + a^2 }}{z = 0} } \\
&=
\lr{ \pi i } \lr{ \frac{e^{-a}}{ia \lr{ 2 i a }} + \inv{2} \frac{1}{a^2}} \\
&=
\frac{\pi i}{2 a^2} \lr{ 1 – e^{-a} }.
\end{aligned}
\end{equation}
Taking the imaginary part of this integral, we have the solution.

What went wrong?

I don’t think there is anything wrong with the residue calculation for “the wrong way”, but it was not correct to argue that the integral along the infinite semicircular arc was zero in that case.

I’d made that argument in the following fashion, looking for the limit of
\begin{equation}\label{eqn:weightedSinc:160}
\begin{aligned}
\int \frac{\sin z}{z \lr{ z^2 + a^2 } } dz
=
\int \frac{e^{iz}}{2 i z \lr{ z^2 + a^2 } } dz –
\int \frac{e^{-iz}}{2 i z \lr{ z^2 + a^2 } } dz
\end{aligned}
\end{equation}
We can apply Jordan’s lemma to the first integral, but not the second. To see why specifically, consider an explicit \( z = R e^{i \theta } \) parameterization of that integral
\begin{equation}\label{eqn:weightedSinc:180}
\begin{aligned}
\Abs{\int \frac{e^{-iz}}{2 i z \lr{ z^2 + a^2 } } dz}
&=
\inv{2} \Abs{ \int_0^\pi \frac{e^{-i R e^{i\theta} }}{R e^{i\theta} \lr{ R^2 e^{2 i \theta} + a^2 } } i R e^{i \theta} d\theta } \\
&=
\inv{2} \Abs{ \int_0^\pi \frac{e^{-i R e^{i\theta} }}{\lr{ R^2 e^{2 i \theta} + a^2 } } d\theta } \\
&=
\inv{2} \Abs{ \int_0^\pi \frac{ e^{-i R \cos\theta} e^{R \sin\theta} }{\lr{ R^2 e^{2 i \theta} + a^2 } } d\theta }.
\end{aligned}
\end{equation}
Not only is this not zero, it’s very obviously infinite for \( R \rightarrow \infty \), as the real exponential will dominate (at least for some angles.) In particular, note that along the imaginary axis, say \( z = i u\), we have \( \sin z = i \sinh u \), which blows up as \( u \rightarrow \infty \). That sine is not well behaved, so we have to use the imaginary part trick, to convert it to an exponential that will submit properly to Jordan’s lemma.

The moral of the story is that if we incorrectly identify that a portion of the contour integral is zero, when it isn’t, the rest of the results that follow are garbage.

References

[1] F.W. Byron and R.W. Fuller. Mathematics of Classical and Quantum Physics. Dover Publications, 1992.