angular momentum

Angular momentum bivector in cylindrical and spherical bases.

September 15, 2022 math and physics play , , , , , , ,

[Click here for a PDF version of this post]

Motivation

In a discord thread on the bivector group (a geometric algebra group chat), MoneyKills posts about trouble he has calculating the correct expression for the angular momentum bivector or it’s dual.

This blog post is a more long winded answer than my bivector response and includes this calculation using both cylindrical and spherical coordinates.

Cylindrical coordinates.

The position vector for any point on a plane can be expressed as
\begin{equation}\label{eqn:amomentum:20}
\Br = r \rcap,
\end{equation}
where \( \rcap = \rcap(\phi) \) encodes all the angular dependence of the position vector, and \( r \) is the length along that direction to our point, as illustrated in fig. 1.

fig. 1. Cylindrical coordinates position vector.

The radial unit vector has a compact GA representation
\begin{equation}\label{eqn:amomentum:40}
\rcap = \Be_1 e^{i\phi},
\end{equation}
where \( i = \Be_1 \Be_2 \).

The velocity (or momentum) will have both \( \rcap \) and \( \phicap \) dependence. By chain rule, that velocity is
\begin{equation}\label{eqn:amomentum:60}
\Bv = \dot{r} \rcap + r \dot{\rcap},
\end{equation}
where
\begin{equation}\label{eqn:amomentum:80}
\begin{aligned}
\dot{\rcap}
&= \Be_1 i e^{i\phi} \dot{\phi} \\
&= \Be_2 e^{i\phi} \dot{\phi} \\
&= \phicap \dot{\phi}.
\end{aligned}
\end{equation}
It is left to the reader to show that the vector designated \( \phicap \), is a unit vector and perpendicular to \( \rcap \) (Hint: compute the grade-0 selection of the product of the two to show that they are perpendicular.)

We can now compute the momentum, which is
\begin{equation}\label{eqn:amomentum:100}
\Bp = m \Bv = m \lr{ \dot{r} \rcap + r \dot{\phi} \phicap },
\end{equation}
and the angular momentum bivector
\begin{equation}\label{eqn:amomentum:120}
\begin{aligned}
L
&= \Br \wedge \Bp \\
&= m \lr{ r \rcap } \wedge \lr{ \dot{r} \rcap + r \dot{\phi} \phicap } \\
&= m r^2 \dot{\phi} \rcap \phicap.
\end{aligned}
\end{equation}

This has the \( m r^2 \dot{\phi} \) magnitude that the OP was seeking.

Spherical coordinates.

In spherical coordinates, our position vector is
\begin{equation}\label{eqn:amomentum:140}
\Br = r \lr{ \Be_1 \sin\theta \cos\phi + \Be_2 \sin\theta \sin\phi + \Be_3 \cos\theta },
\end{equation}
as sketched in fig. 2.

fig. 2. Spherical coordinates.

We can factor this into a more compact representation
\begin{equation}\label{eqn:amomentum:160}
\begin{aligned}
\Br
&= r \lr{ \sin\theta \Be_1 (\cos\phi + \Be_{12} \sin\phi ) + \Be_3 \cos\theta } \\
&= r \lr{ \sin\theta \Be_1 e^{\Be_{12} \phi } + \Be_3 \cos\theta } \\
&= r \Be_3 \lr{ \cos\theta + \sin\theta \Be_3 \Be_1 e^{\Be_{12} \phi } }.
\end{aligned}
\end{equation}

It is useful to name two of the bivector terms above, first, we write \( i \) for the azimuthal plane bivector sketched in fig. 3.

Spherical coordinates, azimuthal plane.

\begin{equation}\label{eqn:amomentum:180}
i = \Be_{12},
\end{equation}
and introduce a bivector \( j \) that encodes the \( \Be_3, \rcap \) plane as sketched in fig. 4.

Spherical coordinates, “j-plane”.

\begin{equation}\label{eqn:amomentum:200}
j = \Be_{31} e^{i \phi}.
\end{equation}

Having done so, we now have a compact representation for our position vector
\begin{equation}\label{eqn:amomentum:220}
\begin{aligned}
\Br
&= r \Be_3 \lr{ \cos\theta + j \sin\theta } \\
&= r \Be_3 e^{j \theta}.
\end{aligned}
\end{equation}

This provides us with a nice compact representation of the radial unit vector
\begin{equation}\label{eqn:amomentum:240}
\rcap = \Be_3 e^{j \theta}.
\end{equation}

Just as was the case in cylindrical coordinates, our azimuthal plane unit vector is
\begin{equation}\label{eqn:amomentum:280}
\phicap = \Be_2 e^{i\phi}.
\end{equation}

Now we want to compute the velocity vector. As was the case in cylindrical coordinates, we have
\begin{equation}\label{eqn:amomentum:300}
\Bv = \dot{r} \rcap + r \dot{\rcap},
\end{equation}
but now we need the spherical representation for the \( \rcap \) derivative, which is
\begin{equation}\label{eqn:amomentum:320}
\begin{aligned}
\dot{\rcap}
&=
\PD{\theta}{\rcap} \dot{\theta} + \PD{\phi}{\rcap} \dot{\phi} \\
&=
\Be_3 e^{j\theta} j \dot{\theta} + \Be_3 \sin\theta \PD{\phi}{j} \dot{\phi} \\
&=
\rcap j \dot{\theta} + \Be_3 \sin\theta j i \dot{\phi}.
\end{aligned}
\end{equation}
We can reduce the second multivector term without too much work
\begin{equation}\label{eqn:amomentum:340}
\begin{aligned}
\Be_3 j i
&=
\Be_3 \Be_{31} e^{i\phi} i \\
&=
\Be_3 \Be_{31} i e^{i\phi} \\
&=
\Be_{33112} e^{i\phi} \\
&=
\Be_{2} e^{i\phi} \\
&= \phicap,
\end{aligned}
\end{equation}
so we have
\begin{equation}\label{eqn:amomentum:360}
\dot{\rcap}
=
\rcap j \dot{\theta} + \sin\theta \phicap \dot{\phi}.
\end{equation}

The velocity is
\begin{equation}\label{eqn:amomentum:380}
\Bv = \dot{r} \rcap + r \lr{ \rcap j \dot{\theta} + \sin\theta \phicap \dot{\phi} }.
\end{equation}

Now we can finally compute the angular momentum bivector, which is
\begin{equation}\label{eqn:amomentum:400}
\begin{aligned}
L &=
\Br \wedge \Bp \\
&=
m r \rcap \wedge \lr{ \dot{r} \rcap + r \lr{ \rcap j \dot{\theta} + \sin\theta \phicap \dot{\phi} } } \\
&=
m r^2 \rcap \wedge \lr{ \rcap j \dot{\theta} + \sin\theta \phicap \dot{\phi} } \\
&=
m r^2 \gpgradetwo{ \rcap \lr{ \rcap j \dot{\theta} + \sin\theta \phicap \dot{\phi} } },
\end{aligned}
\end{equation}
which is just
\begin{equation}\label{eqn:amomentum:420}
L =
m r^2 \lr{ j \dot{\theta} + \sin\theta \rcap \phicap \dot{\phi} }.
\end{equation}

I was slightly surprised by this result, as I naively expected the cylindrical coordinate result. We have a \( m r^2 \rcap \phicap \dot{\phi} \) term, as was the case in cylindrical coordinates, but scaled down with a \( \sin\theta \) factor. However, this result does make sense. Consider for example, some fixed circular motion with \( \theta = \mathrm{constant} \), as sketched in fig. 5.

fig. 5. Circular motion for constant theta

The radius of this circle is actually \( r \sin\theta \), so the total angular momentum for that motion is scaled down to \( m r^2 \sin\theta \dot{\phi} \), smaller than the maximum circular angular momentum of \( m r^2 \dot{\phi} \) which occurs in the \( \theta = \pi/2 \) azimuthal plane. Similarly, if we have circular motion in the “j-plane”, sketched in fig. 6.

fig. 6. Circular motion for constant phi.

where \( \phi = \mathrm{constant} \), then our angular momentum is \( L = m r^2 j \dot{\theta} \).

PHY2403H Quantum Field Theory. Lecture 9: Unbroken and spontaneously broken symmetries, Higgs Lagrangian, scale invariance, Lorentz invariance, angular momentum quantization. Taught by Prof. Erich Poppitz

October 11, 2018 phy2403 , , , , , , , , , , , , , , ,

[Click here for a PDF of this post with nicer formatting (and a Mathematica listing that I didn’t include in this blog post’s latex export)]

DISCLAIMER: Very rough notes from class, with some additional side notes.

These are notes for the UofT course PHY2403H, Quantum Field Theory I, taught by Prof. Erich Poppitz fall 2018.

Last time

We followed a sequence of operations

  1. Noether’s theorem
  2. \( \rightarrow \) conserved currents
  3. \( \rightarrow \) charges (classical)
  4. \( \rightarrow \) “correspondence principle”
  5. \( \rightarrow \hatQ \)
  • Hermitian operators
  • “generators of symmetry”
    \begin{equation}\label{eqn:qftLecture9:20}
    \hatU(\alpha) = e^{i \alpha \hatQ}
    \end{equation}
    We found
    \begin{equation}\label{eqn:qftLecture9:40}
    \hatU(\alpha) \phihat \hatU^\dagger(\alpha) = \phihat + i \alpha \antisymmetric{\hatQ}{\phihat} + \cdots
    \end{equation}

Example: internal symmetries:

(non-spacetime), such as \( O(N)\) or \( U(1) \).

In QFT internal symmetries can have different “\underline{modes of realization}”.

    [I]

  1. “Wigner mode”. These are also called “unbroken symmetries”.
    \begin{equation}\label{eqn:qftLecture9:60}
    \hatQ \ket{0} = 0
    \end{equation}
    i.e. \( \hatU(\alpha) \ket{0} = 0 \).
    Ground state invariant. Formally \( :\hatQ: \) annihilates \( \ket{0} \).
    \( \antisymmetric{\hatQ}{\hatH} = 0 \) implies that all eigenstates are eigenstates of \( \hatQ \) in \( U(1) \). Example from HW 1
    \begin{equation}\label{eqn:qftLecture9:80}
    \hatQ = \text{“charge” under \( U(1) \)}.
    \end{equation}
    All states have definite charge, just live in QU.
  2. “Nambu-Goldstone mode” (Landau-ginsburg). This is also called a “spontaneously broken symmetry”\footnote{
    First encounter example (HWII, \( SU(2) \times SU(2) \rightarrow SU(2) \)). Here a \( U(1) \) spontaneous broken symmetry.}.
    \( H \) or \( L \) is invariant under symmetry, but ground state is not.

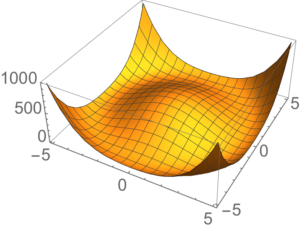
fig. 1. Mexican hat potential.

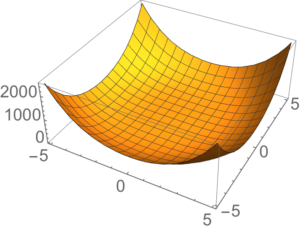
fig. 2. Degenerate Mexican hat potential ( v = 0)

Example:
\begin{equation}\label{eqn:qftLecture9:100}
\LL = \partial_\mu \phi^\conj \partial^\mu \phi – V(\Abs{\phi}),
\end{equation}
where
\begin{equation}\label{eqn:qftLecture9:120}
V(\Abs{\phi}) = m^2 \phi^\conj \phi + \frac{\lambda}{4} \lr{ \phi^\conj \phi }^2.
\end{equation}
When \( m^2 > 0 \) we have a Wigner mode, but when \( m^2 < 0 \) we have an issue: \( \phi = 0 \) is not a minimum of potential.
When \( m^2 < 0 \) we write
\begin{equation}\label{eqn:qftLecture9:140}
\begin{aligned}
V(\phi)
&= – m^2 \phi^\conj \phi + \frac{\lambda}{4} \lr{ \phi^\conj \phi}^2 \\
&= \frac{\lambda}{4} \lr{
\lr{ \phi^\conj \phi}^2 – \frac{4}{\lambda} m^2 } \\
&= \frac{\lambda}{4} \lr{
\phi^\conj \phi – \frac{2}{\lambda} m^2 }^2 – \frac{4 m^4}{\lambda^2},
\end{aligned}
\end{equation}
or simply
\begin{equation}\label{eqn:qftLecture9:780}
V(\phi)
=
\frac{\lambda}{4} \lr{ \phi^\conj \phi – v^2 }^2 + \text{const}.
\end{equation}
The potential (called the Mexican hat potential) is illustrated in fig. 1 for non-zero \( v \), and in
fig. 2 for \( v = 0 \).
We choose to expand around some point on the minimum ring (it doesn’t matter which one).
When there is no potential, we call the field massless (i.e. if we are in the minimum ring).
We expand as
\begin{equation}\label{eqn:qftLecture9:160}
\phi(x) = v \lr{ 1 + \frac{\rho(x)}{v} } e^{i \alpha(x)/v },
\end{equation}
so
\begin{equation}\label{eqn:qftLecture9:180}
\begin{aligned}
\frac{\lambda}{4}
\lr{\phi^\conj \phi – v^2}^2
&=
\lr{
v^2 \lr{ 1 + \frac{\rho(x)}{v} }^2
– v^2
}^2 \\
&=
\frac{\lambda}{4}
v^4 \lr{ \lr{ 1 + \frac{\rho(x)}{v} }^2 – 1 } \\
&=
\frac{\lambda}{4}
v^4
\lr{
\frac{2 \rho}{v} + \frac{\rho^2}{v^2}
}^2.
\end{aligned}
\end{equation}

\begin{equation}\label{eqn:qftLecture9:200}
\partial_\mu \phi =
\lr{
v \lr{ 1 + \frac{\rho(x)}{v} } \frac{i}{v} \partial_\mu \alpha
+ \partial_\mu \rho
} e^{i \alpha}
\end{equation}

so
\begin{equation}\label{eqn:qftLecture9:220}
\begin{aligned}
\LL
&= \Abs{\partial \phi^\conj}^2 – \frac{\lambda}{4} \lr{ \Abs{\phi^\conj}^2 – v^2 }^2 \\
&=
\partial_\mu \rho \partial^\mu \rho + \partial_\mu \alpha \partial^\mu \alpha \lr{ 1 + \frac{\rho}{v} }
–
\frac{\lambda v^4}{4} \frac{ 4\rho^2}{v^2} + O(\rho^3) \\
&=
\partial_\mu \rho \partial^\mu \rho
– \lambda v^2\rho^2
+
\partial_\mu \alpha \partial^\mu \alpha \lr{ 1 + \frac{\rho}{v} }.
\end{aligned}
\end{equation}
We have two fields, \( \rho \) : a massive scalar field, the “Higgs”, and a massless field \( \alpha \) (the Goldstone Boson).

\( U(1) \) symmetry acts on \( \phi(x) \rightarrow e^{i \omega } \phi(x) \) i.t.o \( \alpha(x) \rightarrow \alpha(x) + v \omega \).
\( U(1) \) global symmetry (broken) acts on the Goldstone field \( \alpha(x) \) by a constant shift. (\(U(1)\) is still a symmetry of the Lagrangian.)

The current of the \( U(1) \) symmetry is:
\begin{equation}\label{eqn:qftLecture9:240}
j_\mu = \partial_\mu \alpha \lr{ 1 + \text{higher dimensional \( \rho \) terms} }.
\end{equation}

When we quantize
\begin{equation}\label{eqn:qftLecture9:260}
\alpha(x) =
\int \frac{d^3p}{(2\pi)^3 \sqrt{ 2 \omega_p }} e^{i \omega_p t – i \Bp \cdot \Bx} \hat{a}_\Bp^\dagger +
\int \frac{d^3p}{(2\pi)^3 \sqrt{ 2 \omega_p }} e^{-i \omega_p t + i \Bp \cdot \Bx} \hat{a}_\Bp
\end{equation}
\begin{equation}\label{eqn:qftLecture9:280}
j^\mu(x) = \partial^\mu \alpha(x) =
\int \frac{d^3p}{(2\pi)^3 \sqrt{ 2 \omega_p }} \lr{ i \omega_\Bp – i \Bp } e^{i \omega_p t – i \Bp \cdot \Bx} \hat{a}_\Bp^\dagger +
\int \frac{d^3p}{(2\pi)^3 \sqrt{ 2 \omega_p }} \lr{ -i \omega_\Bp + i \Bp } e^{-i \omega_p t + i \Bp \cdot \Bx} \hat{a}_\Bp.
\end{equation}

\begin{equation}\label{eqn:qftLecture9:300}
j^\mu(x) \ket{0} \ne 0,
\end{equation}
instead it creates a single particle state.

Examples of symmetries

In particle physics, examples of Wigner vs Nambu-Goldstone, ignoring gravity the only exact internal symmetry in the standard module is
\( (B\# – L\#) \), believed to be a \( U(1) \) symmetry in Wigner mode.

Here \(B\#\) is the Baryon number, and \( L\# \) is the Lepton number. Examples:

  • \( B(p) = 1 \), proton.
  • \( B(q) = 1/3 \), quark
  • \( B(e) = 1 \), electron
  • \( B(n) = 1 \), neutron.
  • \( L(p) = 1 \), proton.
  • \( L(q) = 0 \), quark.
  • \( L(e) = 0 \), electron.

The major use of global internal symmetries in the standard model is as “approximate” ones. They become symmetries when one neglects some effect( “terms in \( \LL \)”).
There are other approximate symmetries (use of group theory to find the Balmer series).

Example from HW2:

QCD in limit
\begin{equation}\label{eqn:qftLecture9:320}
m_u = m_d = 0.
\end{equation}
\( m_u m_d \ll m_p \) (the products of the up-quark mass and the down-quark mass are much less than a composite one (name?)).
\( SU(2)_L \times SU(2)_R \rightarrow SU(2)_V \)

EWSB (Electro-Weak-Symmetry-Breaking) sector

When the couplings \( g_2, g_1 = 0 \). (\( g_2 \in SU(2), g_1 \in U(1) \)).

Scale invariance

\begin{equation}\label{eqn:qftLecture9:340}
\begin{aligned}
x &\rightarrow e^{\lambda} x \\
\phi &\rightarrow e^{-\lambda} \phi \\
A_\mu &\rightarrow e^{-\lambda} A_\mu
\end{aligned}
\end{equation}
Any unitary theory which is scale invariant is also \underline{conformal} invariant. Conformal invariance means that angles are preserved.
The point here is that there is more than scale invariance.

We have classical internal global continuous symmetries.
These can be either

  1. “unbroken” (Wigner mode)
    \begin{equation}\label{eqn:qftLecture9:360}
    \hatQ\ket{0} = 0.
    \end{equation}
  2. “spontaneously broken”
    \begin{equation}\label{eqn:qftLecture9:380}
    j^\mu(x) \ket{0} \ne 0
    \end{equation}
    (creates Goldstone modes).
  3. “anomalous”. Classical symmetries are not a symmetry of QFT.
    Examples:

    • Scale symmetry (to be studied in QFT II), although this is not truly internal.
    • In QCD again when \( \omega_\Bq = 0 \), a \( U(1\) symmetry (chiral symmetry) becomes exact, and cannot be preserved in QFT.
    • In the standard model (E.W sector), the Baryon number and Lepton numbers are not symmetries, but their difference \( B\# – L\# \) is a symmetry.

Lorentz invariance.

We’d like to study the action of Lorentz symmetries on quantum states. We are going to “go by the book”, finding symmetries, currents, quantize, find generators, and so forth.

Under a Lorentz transformation
\begin{equation}\label{eqn:qftLecture9:400}
x^\mu \rightarrow {x’}^\mu = {\Lambda^\mu}_\nu x^\nu,
\end{equation}
We are going to consider infinitesimal Lorentz transformations
\begin{equation}\label{eqn:qftLecture9:420}
{\Lambda^\mu}_\nu \approx
{\delta^\mu}_\nu + {\omega^\mu}_\nu
,
\end{equation}
where \( {\omega^\mu}_\nu \) is small.
A Lorentz transformation \( \Lambda \) must satisfy \( \Lambda^\T G \Lambda = G \), or
\begin{equation}\label{eqn:qftLecture9:800}
g_{\mu\nu} = {{\Lambda}^\alpha}_\mu g_{\alpha \beta} {{\Lambda}^\beta}_\nu,
\end{equation}
into which we insert the infinitesimal transformation representation
\begin{equation}\label{eqn:qftLecture9:820}
\begin{aligned}
0
&=
– g_{\mu\nu} +
\lr{ {\delta^\alpha}_\mu + {\omega^\alpha}_\mu }
g_{\alpha \beta}
\lr{ {\delta^\beta}_\nu + {\omega^\beta}_\nu } \\
&=
– g_{\mu\nu} +
\lr{
g_{\mu \beta}
+
\omega_{\beta\mu}
}
\lr{ {\delta^\beta}_\nu + {\omega^\beta}_\nu } \\
&=
– g_{\mu\nu} +
g_{\mu \nu}
+
\omega_{\nu\mu}
+
\omega_{\mu\nu}
+
\omega_{\beta\mu}
{\omega^\beta}_\nu.
\end{aligned}
\end{equation}
The quadratic term can be ignored, leaving just
\begin{equation}\label{eqn:qftLecture9:840}
0 =
\omega_{\nu\mu}
+
\omega_{\mu\nu},
\end{equation}
or
\begin{equation}\label{eqn:qftLecture9:860}
\omega_{\nu\mu} = – \omega_{\mu\nu}.
\end{equation}
Note that \( \omega \) is a completely antisymmetric tensor, and like \( F_{\mu\nu} \) this has only 6 elements.
This means that the
infinitesimal transformation of the coordinates is
\begin{equation}\label{eqn:qftLecture9:440}
x^\mu \rightarrow {x’}^\mu \approx x^\mu + \omega^{\mu\nu} x_\nu,
\end{equation}
the field transforms as
\begin{equation}\label{eqn:qftLecture9:460}
\phi(x) \rightarrow \phi'(x’) = \phi(x)
\end{equation}
or
\begin{equation}\label{eqn:qftLecture9:760}
\phi'(x^\mu + \omega^{\mu\nu} x_\nu) =
\phi'(x) + \omega^{\mu\nu} x_\nu \partial_\mu\phi(x) = \phi(x),
\end{equation}
so
\begin{equation}\label{eqn:qftLecture9:480}
\delta \phi = \phi'(x) – \phi(x) =
-\omega^{\mu\nu} x_\nu \partial_\mu \phi.
\end{equation}

Since \( \LL \) is a scalar
\begin{equation}\label{eqn:qftLecture9:500}
\begin{aligned}
\delta \LL
&=
-\omega^{\mu\nu} x_\nu \partial_\mu \LL \\
&=
–
\partial_\mu \lr{
\omega^{\mu\nu} x_\nu \LL
}
+
(\partial_\mu x_\nu) \omega^{\mu\nu} \LL \\
&=
\partial_\mu \lr{
–
\omega^{\mu\nu} x_\nu \LL
},
\end{aligned}
\end{equation}
since \( \partial_\nu x_\mu = g_{\nu\mu} \) is symmetric, and \( \omega \) is antisymmetric.
Our current is
\begin{equation}\label{eqn:qftLecture9:520}
J^\mu_\omega
=
–
\omega^{\mu\nu} x_\mu \LL
.
\end{equation}
Our Noether current is
\begin{equation}\label{eqn:qftLecture9:540}
\begin{aligned}
j^\nu_{\omega^{\mu\rho}}
&= \PD{\phi_{,\nu}}{\LL} \delta \phi – J^\mu_\omega \\
&=
\partial^\nu \phi\lr{ – \omega^{\mu\rho} x_\rho \partial_\mu \phi } + \omega^{\nu \rho} x_\rho \LL \\
&=
\omega^{\mu\rho}
\lr{
\partial^\nu \phi\lr{ – x_\rho \partial_\mu \phi } + {\delta^{\nu}}_\mu x_\rho \LL
} \\
&=
\omega^{\mu\rho} x_\rho
\lr{
-\partial^\nu \phi \partial_\mu \phi + {\delta^{\nu}}_\mu \LL
}
\end{aligned}
\end{equation}
We identify
\begin{equation}\label{eqn:qftLecture9:560}
–
{T^\nu}_\mu =
-\partial^\nu \phi \partial_\mu \phi + {\delta^{\nu}}_\mu \LL,
\end{equation}
so the current is
\begin{equation}\label{eqn:qftLecture9:580}
\begin{aligned}
j^\nu_{\omega_{\mu\rho}}
&=
-\omega^{\mu\rho} x_\rho
{T^\nu}_\mu \\
&=
-\omega_{\mu\rho} x^\rho
T^{\nu\mu}
.
\end{aligned}
\end{equation}
Define
\begin{equation}\label{eqn:qftLecture9:600}
j^{\nu\mu\rho} = \inv{2} \lr{ x^\rho T^{\nu\mu} – x^{\mu} T^{\nu\rho} },
\end{equation}
which retains the antisymmetry in \( \mu \rho \) yet still drops the parameter \( \omega^{\mu\rho} \).
To check that this makes sense, we can contract
\( j^{\nu\mu\rho} \) with \( \omega_{\rho\mu} \)
\begin{equation}\label{eqn:qftLecture9:880}
\begin{aligned}
j^{\nu\mu\rho} \omega_{\rho\mu}
&= -\inv{2} \lr{ x^\rho T^{\nu\mu} – x^{\mu} T^{\nu\rho} }
\omega_{\mu\rho} \\
&=
-\inv{2} x^\rho T^{\nu\mu}
\omega_{\mu\rho}
– \inv{2} x^{\mu} T^{\nu\rho}
\omega_{\rho\mu} \\
&=
-\inv{2} x^\rho T^{\nu\mu}
\omega_{\mu\rho}
– \inv{2} x^{\rho} T^{\nu\mu}
\omega_{\mu\rho} \\
&=
– x^{\rho} T^{\nu\mu}
\omega_{\mu\rho},
\end{aligned}
\end{equation}
which matches \ref{eqn:qftLecture9:580} as desired.

Example. Rotations \( \mu\rho = ij \)

\begin{equation}\label{eqn:qftLecture9:620}
\begin{aligned}
J^{0 i j} \epsilon_{ijk}
&=
\inv{2} \lr{ x^i T^{0j} – x^{j} T^{0i} } \epsilon_{ijk} \\
&=
x^i T^{0j} \epsilon_{ijk}.
\end{aligned}
\end{equation}
Observe that this has the structure of \( (\Bx \cross \Bp)_k \), where \( \Bp \) is the momentum density of the field.
Let
\begin{equation}\label{eqn:qftLecture9:640}
L_k \equiv Q_k = \int d^3 x J^{0ij} \epsilon_{ijk}.
\end{equation}
We can now quantize and build a generator
\begin{equation}\label{eqn:qftLecture9:660}
\begin{aligned}
\hatU(\Balpha)
&= e^{i \Balpha \cdot \hat{\BL}} \\
&= \exp\lr{i \alpha_k
\int d^3 x x^i \hat{T}^{0j} \epsilon_{ijk}
}
\end{aligned}
\end{equation}
From \ref{eqn:qftLecture9:560} we can quantize with \( T^{0j} = \partial^0 \phi \partial^j \phi \rightarrow \hat{\pi} \lr{\spacegrad \phihat}_j\), or
\begin{equation}\label{eqn:qftLecture9:900}
\begin{aligned}
\hatU(\Balpha)
&=
\exp\lr{i \alpha_k
\int d^3 x x^i \hat{\pi} (\spacegrad \phihat)_j \epsilon_{ijk}
} \\
&=
\exp\lr{i \Balpha \cdot
\int d^3 x \hat{\pi} \spacegrad \phihat \cross \Bx
}
\end{aligned}
\end{equation}
(up to a sign in the exponent which doesn’t matter)
\begin{equation}\label{eqn:qftLecture9:680}
\begin{aligned}
\phihat(\By) \rightarrow \hatU(\alpha) \phihat(\By) \hatU^\dagger(\alpha)
&\approx
\phihat(\By) +
i \Balpha \cdot
\antisymmetric{
\int d^3 x \hat{\pi}(\Bx) \spacegrad \phihat(\Bx) \cross \Bx
}
{
\phihat(\By)
} \\
&=
\phihat(\By) +
i \Balpha \cdot
\int d^3 x
(-i) \delta^3(\Bx – \By)
\spacegrad \phihat(\Bx) \cross \Bx \\
&=
\phihat(\By) +
\Balpha \cdot \lr{ \spacegrad \phihat(\By ) \cross \By}
\end{aligned}
\end{equation}
Explicitly, in coordinates, this is
\begin{equation}\label{eqn:qftLecture9:700}
\begin{aligned}
\phihat(\By)
&\rightarrow
\phihat(\By) +
\alpha^i
\lr{
\partial^j \phihat(\By) y^k \epsilon_{jki}
} \\
&=
\phihat(\By) –
\epsilon_{ikj} \alpha^i y^k \partial^j \phihat \\
&=
\phihat( y^j – \epsilon^{ikj} \alpha^i y^k ).
\end{aligned}
\end{equation}
This is a rotation. To illustrate, pick \( \Balpha = (0, 0, \alpha) \), so \( y^j \rightarrow y^j – \epsilon^{ikj} \alpha y^k \delta_{i3} = y^j – \epsilon^{3kj} \alpha y^k \), or
\begin{equation}\label{eqn:qftLecture9:n}
\begin{aligned}
y^1 &\rightarrow y^1 – \epsilon^{3k1} \alpha y^k = y^1 + \alpha y^2 \\
y^2 &\rightarrow y^2 – \epsilon^{3k2} \alpha y^k = y^2 – \alpha y^1 \\
y^3 &\rightarrow y^3 – \epsilon^{3k3} \alpha y^k = y^3,
\end{aligned}
\end{equation}
or in matrix form
\begin{equation}\label{eqn:qftLecture9:720}
\begin{bmatrix}
y^1 \\
y^2 \\
y^3 \\
\end{bmatrix}
\rightarrow
\begin{bmatrix}
1 & \alpha & 0 \\
-\alpha & 1 & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
y^1 \\
y^2 \\
y^3 \\
\end{bmatrix}.
\end{equation}

Totally asymmetric potential

December 16, 2015 phy1520 , , ,

[Click here for a PDF of this post with nicer formatting]

Q: [1] pr 4.11

(a) Given a time reversal invariant Hamiltonian, show that for any energy eigenket

\begin{equation}\label{eqn:totallyAsymmetricPotential:20}
\expectation{\BL} = 0.
\end{equation}

(b) If the wave function of such a state is expanded as

\begin{equation}\label{eqn:totallyAsymmetricPotential:40}
\sum_{l,m} F_{l m} Y_{l m}(\theta, \phi),
\end{equation}

what are the phase restrictions on \( F_{lm} \)?

A: part (a)

For a time reversal invariant Hamiltonian \( H \) we have

\begin{equation}\label{eqn:totallyAsymmetricPotential:60}
H \Theta = \Theta H.
\end{equation}

If \( \ket{\psi} \) is an energy eigenstate with eigenvalue \( E \), we have

\begin{equation}\label{eqn:totallyAsymmetricPotential:80}
\begin{aligned}
H \Theta \ket{\psi}
&= \Theta H \ket{\psi} \\
&= \lambda \Theta \ket{\psi},
\end{aligned}
\end{equation}

so \( \Theta \ket{\psi} \) is also an eigenvalue of \( H \), so can only differ from \( \ket{\psi} \) by a phase factor. That is

\begin{equation}\label{eqn:totallyAsymmetricPotential:100}
\begin{aligned}
\ket{\psi’}
&=
\Theta \ket{\psi} \\
&= e^{i\delta} \ket{\psi}.
\end{aligned}
\end{equation}

Now consider the expectation of \( \BL \) with respect to a time reversed state

\begin{equation}\label{eqn:totallyAsymmetricPotential:120}
\begin{aligned}
\bra{ \psi’} \BL \ket{\psi’}
&=
\bra{ \psi} \Theta^{-1} \BL \Theta \ket{\psi} \\
&=
\bra{ \psi} (-\BL) \ket{\psi},
\end{aligned}
\end{equation}

however, we also have

\begin{equation}\label{eqn:totallyAsymmetricPotential:140}
\begin{aligned}
\bra{ \psi’} \BL \ket{\psi’}
&=
\lr{ \bra{ \psi} e^{-i\delta} } \BL \lr{ e^{i\delta} \ket{\psi} } \\
&=
\bra{\psi} \BL \ket{\psi},
\end{aligned}
\end{equation}

so we have \( \bra{\psi} \BL \ket{\psi} = -\bra{\psi} \BL \ket{\psi} \) which is only possible if \( \expectation{\BL} = \bra{\psi} \BL \ket{\psi} = 0\).

A: part (b)

Consider the expansion of the wave function of a time reversed energy eigenstate

\begin{equation}\label{eqn:totallyAsymmetricPotential:160}
\begin{aligned}
\bra{\Bx} \Theta \ket{\psi}
&=
\bra{\Bx} e^{i\delta} \ket{\psi} \\
&=
e^{i\delta} \braket{\Bx}{\psi},
\end{aligned}
\end{equation}

and then consider the same state expanded in the position basis

\begin{equation}\label{eqn:totallyAsymmetricPotential:180}
\begin{aligned}
\bra{\Bx} \Theta \ket{\psi}
&=
\bra{\Bx} \Theta \int d^3 \Bx’ \lr{ \ket{\Bx’}\bra{\Bx’} } \ket{\psi} \\
&=
\bra{\Bx} \Theta \int d^3 \Bx’ \lr{ \braket{\Bx’}{\psi} } \ket{\Bx’} \\
&=
\bra{\Bx} \int d^3 \Bx’ \lr{ \braket{\Bx’}{\psi} }^\conj \Theta \ket{\Bx’} \\
&=
\bra{\Bx} \int d^3 \Bx’ \lr{ \braket{\Bx’}{\psi} }^\conj \ket{\Bx’} \\
&=
\int d^3 \Bx’ \lr{ \braket{\Bx’}{\psi} }^\conj \braket{\Bx}{\Bx’} \\
&=
\int d^3 \Bx’ \braket{\psi}{\Bx’} \delta(\Bx- \Bx’) \\
&=
\braket{\psi}{\Bx}.
\end{aligned}
\end{equation}

This demonstrates a relationship between the wave function and its complex conjugate

\begin{equation}\label{eqn:totallyAsymmetricPotential:200}
\braket{\Bx}{\psi} = e^{-i\delta} \braket{\psi}{\Bx}.
\end{equation}

Now expand the wave function in the spherical harmonic basis

\begin{equation}\label{eqn:totallyAsymmetricPotential:220}
\begin{aligned}
\braket{\Bx}{\psi}
&=
\int d\Omega \braket{\Bx}{\ncap}\braket{\ncap}{\psi} \\
&=
\sum_{lm} F_{lm}(r) Y_{lm}(\theta, \phi) \\
&=
e^{-i\delta}
\lr{
\sum_{lm} F_{lm}(r) Y_{lm}(\theta, \phi) }^\conj \\
&=
e^{-i\delta}
\sum_{lm} \lr{ F_{lm}(r)}^\conj Y_{lm}^\conj(\theta, \phi) \\
&=
e^{-i\delta}
\sum_{lm} \lr{ F_{lm}(r)}^\conj (-1)^m Y_{l,-m}(\theta, \phi) \\
&=
e^{-i\delta}
\sum_{lm} \lr{ F_{l,-m}(r)}^\conj (-1)^m Y_{l,m}(\theta, \phi),
\end{aligned}
\end{equation}

so the \( F_{lm} \) functions are constrained by

\begin{equation}\label{eqn:totallyAsymmetricPotential:240}
F_{lm}(r) = e^{-i\delta} \lr{ F_{l,-m}(r)}^\conj (-1)^m.
\end{equation}

References

[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.

Angular momentum expectation values

December 14, 2015 phy1520 ,

[Click here for a PDF of this post with nicer formatting]

Q: [1] pr 3.18

Compute the expectation values for the first and second powers of the angular momentum operators with respect to states \( \ket{lm} \).

A:

We can write the expectation values for the \( L_z \) powers immediately

\begin{equation}\label{eqn:angularMomentumExpectation:20}
\expectation{L_z}
= m \Hbar,
\end{equation}

and

\begin{equation}\label{eqn:angularMomentumExpectation:40}
\expectation{L_z^2} = (m \Hbar)^2.
\end{equation}

For the x and y components first express the operators in terms of the ladder operators.

\begin{equation}\label{eqn:angularMomentumExpectation:60}
\begin{aligned}
L_{+} &= L_x + i L_y \\
L_{-} &= L_x – i L_y.
\end{aligned}
\end{equation}

Rearranging gives

\begin{equation}\label{eqn:angularMomentumExpectation:80}
\begin{aligned}
L_x &= \inv{2} \lr{ L_{+} + L_{-} } \\
L_y &= \inv{2i} \lr{ L_{+} – L_{-} }.
\end{aligned}
\end{equation}

The first order expectations \( \expectation{L_x}, \expectation{L_y} \) are both zero since \( \expectation{L_{+}} = \expectation{L_{-}} \). For the second order expectation values we have

\begin{equation}\label{eqn:angularMomentumExpectation:100}
\begin{aligned}
L_x^2
&= \inv{4} \lr{ L_{+} + L_{-} } \lr{ L_{+} + L_{-} } \\
&= \inv{4} \lr{ L_{+} L_{+} + L_{-} L_{-} + L_{+} L_{-} + L_{-} L_{+} } \\
&= \inv{4} \lr{ L_{+} L_{+} + L_{-} L_{-} + 2 (L_x^2 + L_y^2) } \\
&= \inv{4} \lr{ L_{+} L_{+} + L_{-} L_{-} + 2 (\BL^2 – L_z^2) },
\end{aligned}
\end{equation}

and
\begin{equation}\label{eqn:angularMomentumExpectation:120}
\begin{aligned}
L_y^2
&= -\inv{4} \lr{ L_{+} – L_{-} } \lr{ L_{+} – L_{-} } \\
&= -\inv{4} \lr{ L_{+} L_{+} + L_{-} L_{-} – L_{+} L_{-} – L_{-} L_{+} } \\
&= -\inv{4} \lr{ L_{+} L_{+} + L_{-} L_{-} – 2 (L_x^2 + L_y^2) } \\
&= -\inv{4} \lr{ L_{+} L_{+} + L_{-} L_{-} – 2 (\BL^2 – L_z^2) }.
\end{aligned}
\end{equation}

Any expectation value \( \bra{lm} L_{+} L_{+} \ket{lm} \) or \( \bra{lm} L_{-} L_{-} \ket{lm} \) will be zero, leaving

\begin{equation}\label{eqn:angularMomentumExpectation:140}
\begin{aligned}
\expectation{L_x^2}
&=
\expectation{L_y^2} \\
&=
\inv{4} \expectation{2 (\BL^2 – L_z^2) } \\
&=
\inv{2} \lr{ \Hbar^2 l(l+1) – (\Hbar m)^2 }.
\end{aligned}
\end{equation}

Observe that we have
\begin{equation}\label{eqn:angularMomentumExpectation:160}
\expectation{L_x^2}
+
\expectation{L_y^2}
+
\expectation{L_z^2}
=
\Hbar^2 l(l+1)
=
\expectation{\BL^2},
\end{equation}

which is the quantum mechanical analogue of the classical scalar equation \( \BL^2 = L_x^2 + L_y^2 + L_z^2 \).

References

[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.

L_z and L^2 eigenvalues and probabilities for a given wave function

December 13, 2015 phy1520 , , , , ,

[Click here for a PDF of this post with nicer formatting]

Q: [1] 3.17

Given a wave function

\begin{equation}\label{eqn:LsquaredLzProblem:20}
\psi(r,\theta, \phi) = f(r) \lr{ x + y + 3 z },
\end{equation}

  • (a) Determine if this wave function is an eigenfunction of \( \BL^2 \), and the value of \( l \) if it is an eigenfunction.

  • (b) Determine the probabilities for the particle to be found in any given \( \ket{l, m} \) state,
  • (c) If it is known that \( \psi \) is an energy eigenfunction with energy \( E \) indicate how we can find \( V(r) \).

A: (a)

Using
\begin{equation}\label{eqn:LsquaredLzProblem:40}
\BL^2
=
-\Hbar^2 \lr{ \inv{\sin^2\theta} \partial_{\phi\phi} + \inv{\sin\theta} \partial_\theta \lr{ \sin\theta \partial_\theta} },
\end{equation}

and

\begin{equation}\label{eqn:LsquaredLzProblem:60}
\begin{aligned}
x &= r \sin\theta \cos\phi \\
y &= r \sin\theta \sin\phi \\
z &= r \cos\theta
\end{aligned}
\end{equation}

it’s a quick computation to show that

\begin{equation}\label{eqn:LsquaredLzProblem:80}
\BL^2 \psi = 2 \Hbar^2 \psi = 1(1 + 1) \Hbar^2 \psi,
\end{equation}

so this function is an eigenket of \( \BL^2 \) with an eigenvalue of \( 2 \Hbar^2 \), which corresponds to \( l = 1 \), a p-orbital state.

(b)

Recall that the angular representation of \( L_z \) is

\begin{equation}\label{eqn:LsquaredLzProblem:100}
L_z = -i \Hbar \PD{\phi},
\end{equation}

so we have

\begin{equation}\label{eqn:LsquaredLzProblem:120}
\begin{aligned}
L_z x &= i \Hbar y \\
L_z y &= – i \Hbar x \\
L_z z &= 0,
\end{aligned}
\end{equation}

The \( L_z \) action on \( \psi \) is

\begin{equation}\label{eqn:LsquaredLzProblem:140}
L_z \psi = -i \Hbar r f(r) \lr{ – y + x }.
\end{equation}

This wave function is not an eigenket of \( L_z \). Expressed in terms of the \( L_z \) basis states \( e^{i m \phi} \), this wave function is

\begin{equation}\label{eqn:LsquaredLzProblem:160}
\begin{aligned}
\psi
&= r f(r) \lr{ \sin\theta \lr{ \cos\phi + \sin\phi} + \cos\theta } \\
&= r f(r) \lr{ \frac{\sin\theta}{2} \lr{ e^{i \phi} \lr{ 1 + \inv{i}} + e^{-i\phi} \lr{ 1 – \inv{i} } } + \cos\theta } \\
&= r f(r) \lr{
\frac{(1-i)\sin\theta}{2} e^{1 i \phi}
+
\frac{(1+i)\sin\theta}{2} e^{- 1 i \phi}
+ \cos\theta e^{0 i \phi}
}
\end{aligned}
\end{equation}

Assuming that \( \psi \) is normalized, the probabilities for measuring \( m = 1,-1,0 \) respectively are

\begin{equation}\label{eqn:LsquaredLzProblem:180}
\begin{aligned}
P_{\pm 1}
&= 2 \pi \rho \Abs{\frac{1\mp i}{2}}^2 \int_0^\pi \sin\theta d\theta \sin^2 \theta \\
&= -2 \pi \rho \int_1^{-1} du (1-u^2) \\
&= 2 \pi \rho \evalrange{ \lr{ u – \frac{u^3}{3} } }{-1}{1} \\
&= 2 \pi \rho \lr{ 2 – \frac{2}{3}} \\
&= \frac{ 8 \pi \rho}{3},
\end{aligned}
\end{equation}

and

\begin{equation}\label{eqn:LsquaredLzProblem:200}
P_{0} = 2 \pi \rho \int_0^\pi \sin\theta \cos\theta = 0,
\end{equation}

where

\begin{equation}\label{eqn:LsquaredLzProblem:220}
\rho = \int_0^\infty r^4 \Abs{f(r)}^2 dr.
\end{equation}

Because the probabilities must sum to 1, this means the \( m = \pm 1 \) states are equiprobable with \( P_{\pm} = 1/2 \), fixing \( \rho = 3/16\pi \), even without knowing \( f(r) \).

(c)

The operator \( r^2 \Bp^2 \) can be decomposed into a \( \BL^2 \) component and some other portions, from which we can write

\begin{equation}\label{eqn:LsquaredLzProblem:240}
\begin{aligned}
H \psi
&= \lr{ \frac{\Bp^2}{2m} + V(r) } \psi \\
&=
\lr{
– \frac{\Hbar^2}{2m} \lr{ \partial_{rr} + \frac{2}{r} \partial_r – \inv{\Hbar^2 r^2} \BL^2 } + V(r) } \psi.
\end{aligned}
\end{equation}

(See: [1] eq. 6.21)

In this case where \( \BL^2 \psi = 2 \Hbar^2 \psi \) we can rearrange for \( V(r) \)

\begin{equation}\label{eqn:LsquaredLzProblem:260}
\begin{aligned}
V(r)
&= E + \inv{\psi} \frac{\Hbar^2}{2m} \lr{ \partial_{rr} + \frac{2}{r} \partial_r – \frac{2}{r^2} } \psi \\
&= E + \inv{f(r)} \frac{\Hbar^2}{2m} \lr{ \partial_{rr} + \frac{2}{r} \partial_r – \frac{2}{r^2} } f(r).
\end{aligned}
\end{equation}

References

[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.

%d bloggers like this: