[Click here for a PDF of this post with nicer formatting]
Total internal reflection
From Snell’s second law we have
\begin{equation}\label{eqn:brewsters:20}
\theta_t = \arcsin\lr{ \frac{n_i}{n_t} \sin\theta_i }.
\end{equation}
This is plotted in fig. 3.
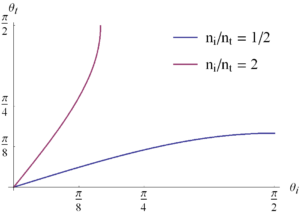
fig. 3. Transmission angle vs incident angle.
For the \( n_i > n_t \) case, for example, like shining from glass into air, there is a critical incident angle beyond which there is no real value of \( \theta_t \). That critical incident angle occurs when \( \theta_t = \pi/2 \), which is
\begin{equation}\label{eqn:brewsters:40}
\sin\theta_{ic} = \frac{n_t}{n_i} \sin(\pi/2).
\end{equation}
With
\begin{equation}\label{eqn:brewsters:340}
n = n_t/n_i
\end{equation}
the critical angle is
\begin{equation}\label{eqn:brewsters:60}
\theta_{ic} = \arcsin n.
\end{equation}
Note that Snell’s law can also be expressed in terms of this critical angle, allowing for the solution of the transmission angle in a convenient way
\begin{equation}\label{eqn:brewsters:360}
\begin{aligned}
\sin\theta_i
&= \frac{n_t}{n_i} \sin\theta_t \\
&= n \sin\theta_t \\
&= \sin\theta_{ic} \sin\theta_t,
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:brewsters:380}
\sin\theta_t = \frac{\sin\theta_i}{\sin\theta_{ic}}.
\end{equation}
Still for \( n_i > n_t \), at angles past \( \theta_{ic} \), the transmitted wave angle becomes complex as outlined in [2], namely
\begin{equation}\label{eqn:brewsters:400}
\begin{aligned}
\cos^2\theta_t
&=
1 – \sin^2 \theta_t \\
&=
1 –
\frac{\sin^2\theta_i}{\sin^2\theta_{ic}} \\
&=
-\lr{
\frac{\sin^2\theta_i}{\sin^2\theta_{ic}}
-1
},
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:brewsters:420}
\cos\theta_t =
j \sqrt{
\frac{\sin^2\theta_i}{\sin^2\theta_{ic}}
-1
}.
\end{equation}
Following the convention that puts the normal propagation direction along z, and the interface along x, the wave vector direction is
\begin{equation}\label{eqn:brewsters:440}
\begin{aligned}
\kcap_t
&= \Be_3 e^{ \Be_{31} \theta_t } \\
&= \Be_3 \cos\theta_t + \Be_1 \sin\theta_t.
\end{aligned}
\end{equation}
The phase factor for the transmitted field is
\begin{equation}\label{eqn:brewsters:460}
\begin{aligned}
\exp\lr{ j \omega t \pm j \Bk_t \cdot \Bx }
&=
\exp\lr{ j \omega t \pm j k \kcap_t \cdot \Bx } \\
&=
\exp\lr{ j \omega t \pm j k \lr{ z \cos\theta_t + x \sin\theta_t } } \\
&=
\exp\lr{
j \omega t
\pm j k \lr{ z j \sqrt{ \frac{\sin^2\theta_i}{\sin^2\theta_{ic}} -1 } + x \frac{\sin\theta_i}{\sin\theta_{ic}} }
} \\
&=
\exp\lr{
j \omega t \pm k
\lr{
j x \frac{\sin\theta_i}{\sin\theta_{ic}}
– z \sqrt{ \frac{\sin^2\theta_i}{\sin^2\theta_{ic}} -1 }
}
}.
\end{aligned}
\end{equation}
The propagation is channelled along the x axis, but the propagation into the second medium decays exponentially (or unphysically grows exponentially), only getting into the surface a small amount.
What is the average power transmission into the medium? We are interested in the time average of the normal component of the Poynting vector \( \BS \cdot \ncap \).
\begin{equation}\label{eqn:brewsters:480}
\begin{aligned}
\BS
&= \inv{2} \BE \cross \BH^\conj \\
&= \inv{2} \BE \cross \lr{ \inv{\eta} \kcap_t \cross \BE^\conj } \\
&= -\inv{2 \eta} \BE \cdot \lr{ \kcap_t \wedge \BE^\conj } \\
&= -\inv{2 \eta} \lr{
(\BE \cdot \kcap_t) \BE^\conj
–
\kcap_t \BE \cdot \BE^\conj
} \\
&=
\inv{2 \eta}
\kcap_t \Abs{\BE}^2.
\end{aligned}
\end{equation}
\begin{equation}\label{eqn:brewsters:500}
\begin{aligned}
\kcap_t \cdot \ncap
&= \lr{ \Be_3 \cos\theta_t + \Be_1 \sin\theta_t } \cdot \Be_3 \\
&= \cos\theta_t \\
&=
j \sqrt{
\frac{\sin^2\theta_i}{\sin^2\theta_{ic}}
-1
}.
\end{aligned}
\end{equation}
Note that this is purely imaginary. The time average real power transmission is
\begin{equation}\label{eqn:brewsters:520}
\begin{aligned}
\expectation{\BS \cdot \ncap}
&=
\textrm{Re} \lr{
j \sqrt{
\frac{\sin^2\theta_i}{\sin^2\theta_{ic}}
-1
}
\frac{1}{2 \eta} \Abs{\BE}^2
} \\
&= 0.
\end{aligned}
\end{equation}
There is no power transmission into the second medium at or past the critical angle for total internal reflection.
Brewster’s angle
Brewster’s angle is the angle for which there the amplitude of the reflected component of the field is zero. Recall that when the electric field is parallel(perpendicular) to the plane of incidence, the reflection amplitude ([1] eq. 4.38)
\begin{equation}\label{eqn:brewsters:80}
r_\parallel
=
\frac
{
\frac{ n_t }{\mu_t} \cos \theta_i
-\frac{ n_i }{\mu_i} \cos \theta_t
}
{
\frac{ n_t }{\mu_t} \cos \theta_i
+\frac{ n_i }{\mu_i} \cos \theta_t
}
\end{equation}
\begin{equation}\label{eqn:brewsters:100}
r_\perp
=
\frac
{
\frac{ n_i }{\mu_i} \cos \theta_i
-\frac{ n_t }{\mu_t} \cos \theta_t
}
{
\frac{ n_i }{\mu_i} \cos \theta_i
+\frac{ n_t }{\mu_t} \cos \theta_t
}
\end{equation}
There are limited conditions for which \( r_\perp \) is zero, at least for \( \mu_i = \mu_t \). Using Snell’s second law \( n_i \sin\theta_i = n_t \sin\theta_t \), that zero is found at
\begin{equation}\label{eqn:brewsters:120}
\begin{aligned}
n_i \cos \theta_i
&= n_t \cos \theta_t \\
&= n_t \sqrt{ 1 – \sin^2 \theta_t } \\
&= n_t \sqrt{ 1 – \frac{n_i^2}{n_t^2} \sin^2 \theta_i },
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:brewsters:140}
\frac{n_i^2}{n_t^2} \cos^2 \theta_i = 1 – \frac{n_i^2}{n_t^2} \sin^2 \theta_i,
\end{equation}
or
\begin{equation}\label{eqn:brewsters:160}
\frac{n_i^2}{n_t^2} \lr{ \cos^2 \theta_i + \sin^2 \theta_i } = 1.
\end{equation}
This has solutions only when \( n_i = \pm n_t \). The \( n_i = n_t \) case is of no interest, since that is just propagation, so naturally there is no reflection. The \( n_i = -n_t \) case is possible with the transmission into a negative index of refraction material that is matched in absolute magnitude with the index of refraction in the incident medium.
There are richer solutions for the \( r_\parallel \) zero. Again considering \( \mu_1 = \mu_2 \) those occur when
\begin{equation}\label{eqn:brewsters:180}
\begin{aligned}
n_t \cos \theta_i
&= n_i \cos \theta_t \\
&= n_i \sqrt{ 1 – \frac{n_i^2}{n_t^2} \sin^2 \theta_i } \\
&= n_i \sqrt{ 1 – \frac{n_i^2}{n_t^2} \sin^2 \theta_i }
\end{aligned}
\end{equation}
Let \( n = n_t/n_i \), and square both sides. This gives
\begin{equation}\label{eqn:brewsters:200}
\begin{aligned}
n^2 \cos^2 \theta_i
&= 1 – \inv{n^2} \sin^2 \theta_i \\
&= 1 – \inv{n^2} (1 – \cos^2 \theta_i),
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:brewsters:220}
\cos^2 \theta_i \lr{ n^2 + \inv{n^2}} = 1 – \inv{n^2},
\end{equation}
or
\begin{equation}\label{eqn:brewsters:240}
\begin{aligned}
\cos^2 \theta_i
&= \frac{1 – \inv{n^2}}{ n^2 – \inv{n^2} } \\
&= \frac{n^2 – 1}{ n^4 – 1 } \\
&= \frac{n^2 – 1}{ (n^2 – 1)(n^2 + 1) } \\
&= \frac{1}{ n^2 + 1 }.
\end{aligned}
\end{equation}
We also have
\begin{equation}\label{eqn:brewsters:260}
\begin{aligned}
\sin^2 \theta_i
&=
1 – \frac{1}{ n^2 + 1 } \\
&=
\frac{n^2}{ n^2 + 1 },
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:brewsters:280}
\tan^2 \theta_i = n^2,
\end{equation}
and
\begin{equation}\label{eqn:brewsters:300}
\tan \theta_{iB} = \pm n,
\end{equation}
For normal media where \( n_i > 0, n_t > 0 \), only the positive solution is physically relevant, which is
\begin{equation}\label{eqn:brewsters:320}
\boxed{
\theta_{iB} = \arctan\lr{ \frac{n_t}{n_i} }.
}
\end{equation}
References
[1] E. Hecht. Optics. 1998.
[2] JD Jackson. Classical Electrodynamics. John Wiley and Sons, 2nd edition, 1975.
Like this:
Like Loading...