[Click here for a PDF of this post with nicer formatting]
Prof. Eleftheriades desribed a Chebychev antenna array design method that looks different than the one of the text [1].
Portions of that procedure are like that of the text. For example, if a side lobe level of \( 20 \log_{10} R \) is desired, a scaling factor
\begin{equation}\label{eqn:chebychevSecondMethod:20}
x_0 = \cosh\lr{ \inv{m} \cosh^{-1} R },
\end{equation}
is used. Given \( N \) elements in the array, a Chebychev polynomial of degree \( m = N – 1 \) is used. That is
\begin{equation}\label{eqn:chebychevSecondMethod:40}
T_m(x) = \cos\lr{ m \cos^{-1} x }.
\end{equation}
Observe that the roots \( x_n’ \) of this polynomial lie where
\begin{equation}\label{eqn:chebychevSecondMethod:60}
m \cos^{-1} x_n’ = \frac{\pi}{2} \pm \pi n,
\end{equation}
or
\begin{equation}\label{eqn:chebychevSecondMethod:80}
x_n’ = \cos\lr{ \frac{\pi}{2 m} \lr{ 2 n \pm 1 } },
\end{equation}
The class notes use the negative sign, and number \( n = 1,2, \cdots, m \). It is noted that the roots are symmetric with \( x_1′ = – x_m’ \), which can be seen by direct expansion
\begin{equation}\label{eqn:chebychevSecondMethod:100}
\begin{aligned}
x_{m-r}’
&= \cos\lr{ \frac{\pi}{2 m} \lr{ 2 (m – r) – 1 } } \\
&= \cos\lr{ \pi – \frac{\pi}{2 m} \lr{ 2 r + 1 } } \\
&= -\cos\lr{ \frac{\pi}{2 m} \lr{ 2 r + 1 } } \\
&= -\cos\lr{ \frac{\pi}{2 m} \lr{ 2 ( r + 1 ) – 1 } } \\
&= -x_{r+1}’.
\end{aligned}
\end{equation}
The next step in the procedure is the identification
\begin{equation}\label{eqn:chebychevSecondMethod:120}
\begin{aligned}
u_n’ &= 2 \cos^{-1} \lr{ \frac{x_n’}{x_0} } \\
z_n &= e^{j u_n’}.
\end{aligned}
\end{equation}
This has a factor of two that does not appear in the Balanis design method. It seems plausible that this factor of two was introduced so that the roots of the array factor \( z_n \) are conjugate pairs. Since \( \cos^{-1} (-z) = \pi – \cos^{-1} z \), this choice leads to such conjugate pairs
\begin{equation}\label{eqn:chebychevSecondMethod:140}
\begin{aligned}
\exp\lr{j u_{m-r}’}
&=
\exp\lr{j 2 \cos^{-1} \lr{ \frac{x_{m-r}’}{x_0} } } \\
&=
\exp\lr{j 2 \cos^{-1} \lr{ -\frac{x_{r+1}’}{x_0} } } \\
&=
\exp\lr{j 2 \lr{ \pi – \cos^{-1} \lr{ \frac{x_{r+1}’}{x_0} } } } \\
&=
\exp\lr{-j u_{r+1}}.
\end{aligned}
\end{equation}
Because of this, the array factor can be written
\begin{equation}\label{eqn:chebychevSecondMethod:180}
\begin{aligned}
\textrm{AF}
&= ( z – z_1 )( z – z_2 ) \cdots ( z – z_{m-1} ) ( z – z_m ) \\
&=
( z – z_1 )( z – z_1^\conj )
( z – z_2 )( z – z_2^\conj )
\cdots \\
&=
\lr{ z^2 – z ( z_1 + z_1^\conj ) + 1 }
\lr{ z^2 – z ( z_2 + z_2^\conj ) + 1 }
\cdots \\
&=
\lr{ z^2 – 2 z \cos\lr{ 2 \cos^{-1} \lr{ \frac{x_1′}{x_0} } } + 1 }
\lr{ z^2 – 2 z \cos\lr{ 2 \cos^{-1} \lr{ \frac{x_2′}{x_0} } } + 1 }
\cdots \\
&=
\lr{ z^2 – 2 z \lr{ 2 \lr{ \frac{x_1′}{x_0} }^2 – 1 } + 1 }
\lr{ z^2 – 2 z \lr{ 2 \lr{ \frac{x_2′}{x_0} }^2 – 1 } + 1 }
\cdots
\end{aligned}
\end{equation}
When \( m \) is even, there will only be such conjugate pairs of roots. When \( m \) is odd, the remainding factor will be
\begin{equation}\label{eqn:chebychevSecondMethod:160}
\begin{aligned}
z – e^{2 j \cos^{-1} \lr{ 0/x_0 } }
&=
z – e^{2 j \pi/2} \\
&=
z – e^{j \pi} \\
&=
z + 1.
\end{aligned}
\end{equation}
However, with this factor of two included, the connection between the final array factor polynomial \ref{eqn:chebychevSecondMethod:180}, and the Chebychev polynomial \( T_m \) is not clear to me. How does this scaling impact the roots?
Example: Expand \( \textrm{AF} \) for \( N = 4 \).
The roots of \( T_3(x) \) are
\begin{equation}\label{eqn:chebychevSecondMethod:200}
x_n’ \in \setlr{0, \pm \frac{\sqrt{3}}{2} },
\end{equation}
so the array factor is
\begin{equation}\label{eqn:chebychevSecondMethod:220}
\begin{aligned}
\textrm{AF}
&=
\lr{ z^2 + z \lr{ 2 – \frac{3}{x_0^2} } + 1 }\lr{ z + 1 } \\
&=
z^3
+ 3 z^2 \lr{ 1 – \frac{1}{x_0^2} }
+ 3 z \lr{ 1 – \frac{1}{x_0^2} }
+ 1.
\end{aligned}
\end{equation}
With \( 20 \log_{10} R = 30 \textrm{dB} \), \( x_0 = 2.1 \), so this is
\begin{equation}\label{eqn:chebychevSecondMethod:240}
\textrm{AF} = z^3 + 2.33089 z^2 + 2.33089 z + 1.
\end{equation}
With
\begin{equation}\label{eqn:chebychevSecondMethod:260}
z = e^{j (u + u_0) } = e^{j k d \cos\theta + j k u_0 },
\end{equation}
the array factor takes the form
\begin{equation}\label{eqn:chebychevSecondMethod:280}
\textrm{AF}
=
e^{j 3 k d \cos\theta + j 3 k u_0 }
+ 2.33089
e^{j 2 k d \cos\theta + j 2 k u_0 }
+ 2.33089
e^{j k d \cos\theta + j k u_0 }
+ 1.
\end{equation}
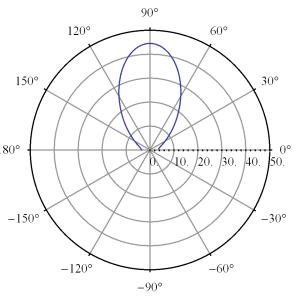
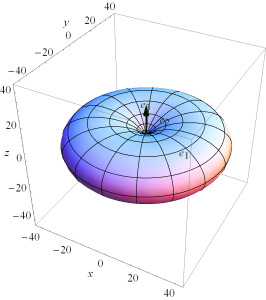
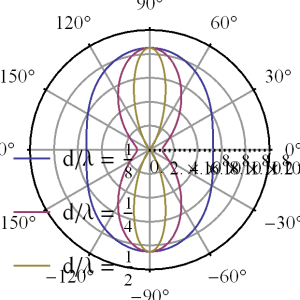
This array function is highly phase dependent, plotted for \( u_0 = 0 \) in fig. 1, and fig. 2.
fig 1. Plot with u_0 = 0, d = lambda/4
fig 2. Spherical plot with u_0 = 0, d = lambda/4
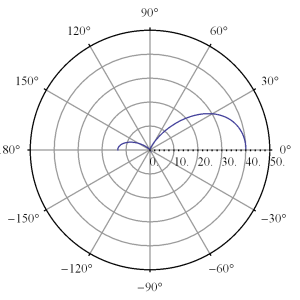
This can be directed along a single direction (z-axis) with higher phase choices as illustrated in fig. 3, and fig. 4.
fig 3. Plot with u_0 = 3.5, d = 0.4 lambda
fig 4. Spherical plot with u_0 = 3.5, d = 0.4 lambda
These can be explored interactively in this Mathematica Manipulate panel.
References
[1] Constantine A Balanis. Antenna theory: analysis and design. John Wiley \& Sons, 3rd edition, 2005.
