[Click here for a PDF of this post with nicer formatting and figures] or [Click here for my notes compilation for this class]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

These are notes for the UofT course ECE1236H, Microwave and Millimeter-Wave
Techniques, taught by Prof. G.V. Eleftheriades, covering [1] chap. 2 content.

Requirements

A transmission line requires two conductors as sketched in fig. 1, which shows a 2-wire line such a telephone line, a coaxial cable as found in cable TV distribution, and a microstrip line as found in cell phone RF interconnects.

../../figures/ece1236/deck4TxlineFig1: fig. 1. Transmission line examples.

A two-wire line becomes a transmission line when the wavelength of operation becomes comparable to the size of the line (or higher spectral component for pulses). In general a transmission line much support (TEM) transverse electromagnetic modes.

Time harmonic solutions on transmission lines

In fig. 2, an electronic representation of a transmission line circuit is sketched.

../../figures/ece1236/deck4TxlineFig2: fig. 2. Transmission line equivalent circuit.

In this circuit all the elements have per-unit length units. With $I = C dV/dt \sim j \omega C V$, $v = I R$, and $V = L dI/dt \sim j \omega L I$, the KVL equation is

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:20} V(z) – V(z + \Delta z) = I(z) \Delta z \lr{ R + j \omega L }, \end{equation}$$

or in the $\Delta z \rightarrow 0$ limit

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:40} \PD{z}{V} = -I(z) \lr{ R + j \omega L }. \end{equation}$$

The KCL equation at the interior node is

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:60} -I(z) + I(z + \Delta z) + \lr{ j \omega C + G} V(z + \Delta z) = 0, \end{equation}$$

or
$$\begin{equation}\label{eqn:uwaves4TransmissionLines:80} \PD{z}{I} = -V(z) \lr{ j \omega C + G}. \end{equation}$$

This pair of equations is known as the telegrapher’s equations

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:100} \boxed{ \begin{aligned} \PD{z}{V} &= -I(z) \lr{ R + j \omega L } \\ \PD{z}{I} &= -V(z) \lr{ j \omega C + G}. \end{aligned} } \end{equation}$$

The second derivatives are

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:120} \begin{aligned} \PDSq{z}{V} &= -\PD{z}{I} \lr{ R + j \omega L } \\ \PDSq{z}{I} &= -\PD{z}{V} \lr{ j \omega C + G}, \end{aligned} \end{equation}$$

which allow the $V, I$ to be decoupled
$$\begin{equation}\label{eqn:uwaves4TransmissionLines:140} \boxed{ \begin{aligned} \PDSq{z}{V} &= V(z) \lr{ j \omega C + G} \lr{ R + j \omega L } \\ \PDSq{z}{I} &= I(z) \lr{ R + j \omega L } \lr{ j \omega C + G}, \end{aligned} } \end{equation}$$

With a complex propagation constant

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:160} \begin{aligned} \gamma &= \alpha + j \beta \\ &= \sqrt{ \lr{ j \omega C + G} \lr{ R + j \omega L } } \\ &= \sqrt{ R G – \omega^2 L C + j \omega ( L G + R C ) }, \end{aligned} \end{equation}$$

the decouple equations have the structure of a wave equation for a lossy line in the frequency domain

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:180} \boxed{ \begin{aligned} \PDSq{z}{V} – \gamma^2 V &= 0 \\ \PDSq{z}{I} – \gamma^2 I &= 0. \end{aligned} } \end{equation}$$

We write the solutions to these equations as

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:200} \begin{aligned} V(z) &= V_0^{+} e^{-\gamma z} + V_0^{-} e^{+\gamma z} \\ I(z) &= I_0^{+} e^{-\gamma z} – I_0^{-} e^{+\gamma z} \\ \end{aligned} \end{equation}$$

Only one of $V$ or $I$ is required since they are dependent through $\ref{eqn:uwaves4TransmissionLines:100}$, as can be seen by taking derivatives

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:220} \begin{aligned} \PD{z}{V} &= \gamma \lr{ -V_0^{+} e^{-\gamma z} + V_0^{-} e^{+\gamma z} } \\ &= -I(z) \lr{ R + j \omega L }, \end{aligned} \end{equation}$$

so
$$\begin{equation}\label{eqn:uwaves4TransmissionLines:240} I(z) = \frac{\gamma}{ R + j \omega L } \lr{ V_0^{+} e^{-\gamma z} – V_0^{-} e^{+\gamma z} }. \end{equation}$$

Introducing the characteristic impedance $Z_0$ of the line

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:260} \begin{aligned} Z_0 &= \frac{R + j \omega L}{\gamma} \\ &= \sqrt{ \frac{R + j \omega L}{G + j \omega C} }, \end{aligned} \end{equation}$$

we have

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:280} \begin{aligned} I(z) &= \inv{Z_0} \lr{ V_0^{+} e^{-\gamma z} – V_0^{-} e^{+\gamma z} } \\ &= I_0^{+} e^{-\gamma z} – I_0^{-} e^{+\gamma z}, \end{aligned} \end{equation}$$

where

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:300} \begin{aligned} I_0^{+} &= \frac{V_0^{+}}{Z_0} \\ I_0^{-} &= \frac{V_0^{-}}{Z_0}. \end{aligned} \end{equation}$$

Mapping TL geometry to per unit length $C$ and $L$ elements

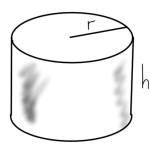
From electrostatics and magnetostatics the per unit length induction and capacitance constants for a co-axial cable can be calculated. For the cylindrical configuration sketched in fig. 3

../../figures/ece1236/deck4TxlineFig3: fig. 3. Coaxial cable.

From Gauss’ law the total charge can be calculated assuming that the ends of the cable can be neglected

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:520} \begin{aligned} Q &= \int \spacegrad \cdot \BD dV \\ &= \oint \BD \cdot d\BA \\ &= \epsilon_0 \epsilon_r E ( 2 \pi r ) l, \end{aligned} \end{equation}$$

This provides the radial electric field magnitude, in terms of the total charge

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:320} E = \frac{Q/l}{\epsilon_0 \epsilon_r ( 2 \pi r ) }, \end{equation}$$

which must be a radial field as sketched in fig. 4.

../../figures/ece1236/deck4TxlineFig4: fig. 4. Radial electric field for coaxial cable.

The potential difference from the inner transmission surface to the outer is

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:340} \begin{aligned} V &= \int_a^b E dr \\ &= \frac{Q/l}{2 \pi \epsilon_0 \epsilon_r } \int_a^b \frac{dr}{r} \\ &= \frac{Q/l}{2 \pi \epsilon_0 \epsilon_r } \ln \frac{b}{a}. \end{aligned} \end{equation}$$

Therefore the capacitance per unit length is

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:360} C = \frac{Q/l}{V} = \frac{2 \pi \epsilon_0 \epsilon_r }{ \ln \frac{b}{a} } . \end{equation}$$

The inductance per unit length can be calculated form Ampere’s law

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:380} \begin{aligned} \int \lr{ \spacegrad \cross \BH } \cdot d\BS &= \int \BJ \cdot d\BS + \PD{t}{} \int \BD \cdot d\Bl \\ &= \int \BJ \cdot d\BS \\ &= I \\ &= \oint \BH \cdot d\Bl \\ &= H ( 2 \pi r ) \\ &= \frac{B}{\mu_0} ( 2 \pi r ) \end{aligned} \end{equation}$$

The flux is

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:400} \begin{aligned} \Phi &= \int \BB \cdot d\BA \\ &= \frac{\mu_0 I}{ 2 \pi } \int_A \inv{r} d dr \\ &= \frac{\mu_0 I}{ 2 \pi } \int_a^b \inv{r} l d dr \\ &= \frac{\mu_0 I l}{ 2 \pi } \ln \frac{b}{a}. \end{aligned} \end{equation}$$

The inductance per unit length is

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:420} L = \frac{\Phi/l}{I} = \frac{\mu_0}{ 2 \pi } \ln \frac{b}{a}. \end{equation}$$

For a lossless line where $R = G = 0$, we have $\gamma = \sqrt{ (j \omega L)(j \omega C)} = j \omega \sqrt{L C}$,
so the phase velocity for a (lossless) coaxial cable is

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:440} \begin{aligned} v_\phi &= \frac{\omega}{\beta} \\ &= \frac{\omega}{\textrm{Im}(\gamma)} \\ &= \frac{\omega}{\omega \sqrt{LC})} \\ &= \frac{1}{\sqrt{LC})}. \end{aligned} \end{equation}$$

This gives

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:460} \begin{aligned} v_\phi^2 &= \inv{ L } \inv{C} \\ &= \frac{ 2 \pi }{ \mu_0 \ln \frac{b}{a} } \frac {\ln \frac{b}{a}} {2 \pi \epsilon_0 \epsilon_r } \\ &= \frac{1 }{ \mu_0 \epsilon_0 \epsilon_r } \\ &= \frac{1 }{ \mu_0 \epsilon }. \end{aligned} \end{equation}$$

So

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:480} v_\phi = \inv{\sqrt{\epsilon \mu_0}}, \end{equation}$$

which is the speed of light in the medium ($\epsilon_r$) that fills the co-axial cable.

This is \underline{not} a coincidence. In any two-wire homogeneously filled transmission line, the phase velocity is equal to the speed of light in the unbounded medium that fills the line.

The characteristic impedance (again assuming the lossless $R = G = 0$ case) is

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:500} \begin{aligned} Z_0 &= \sqrt{ \frac{R + j \omega L}{G + j \omega C} } \\ &= \sqrt{ \frac{j \omega L}{j \omega C} } \\ &= \sqrt{ \frac{L}{C} } \\ &= \sqrt{ \frac{\mu_0}{ 2 \pi } \ln \frac{b}{a} \frac{ \ln \frac{b}{a} }{2 \pi \epsilon_0 \epsilon_r } } \\ &= \sqrt{ \frac{\mu_0}{\epsilon} } \frac{ \ln \frac{b}{a} }{ 2 \pi }. \end{aligned} \end{equation}$$

Note that $\eta = \sqrt{\mu_0/\epsilon_0} = 120 \pi \Omega$ is the intrinsic impedance of free space. The values $a, b$ in $\ref{eqn:uwaves4TransmissionLines:500}$ can be used to tune the characteristic impedance of the transmission line.

Lossless line.

The lossless lossless case where $R = G = 0$ was considered above. The results were

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:540} \gamma = j \omega \sqrt{ L C }, \end{equation}$$

so $\alpha = 0$ and $\beta = \omega \sqrt{LC}$, and the phase velocity was

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:560} v_\phi = \inv{\sqrt{LC}}, \end{equation}$$

the characteristic impedance is

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:580} Z_0 = \sqrt{\frac{L}{C}}, \end{equation}$$

and the signals are
$$\begin{equation}\label{eqn:uwaves4TransmissionLines:600} \begin{aligned} V(z) &= V_0^{+} e^{-j \beta z} + V_0^{-} e^{j \beta z} \\ I(z) &= \inv{Z_0} \lr{ V_0^{+} e^{-j \beta z} – V_0^{-} e^{j \beta z} } \end{aligned} \end{equation}$$

In the time domain for an infinite line, we have

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:620} \begin{aligned} v(z, t) &= \textrm{Re}\lr{ V(z) e^{j \omega t} } \\ &= V_0^{+} \textrm{Re}\lr{ e^{-j \beta z} e^{j \omega t} } \\ &= V_0^{+} \cos( \omega t – \beta z ). \end{aligned} \end{equation}$$

In this case the shape and amplitude of the waveform are preserved as sketched in fig. 7.

../../figures/ece1236/deck4TxlineFig7: fig. 7. Lossless line signal preservation.

Low loss line.

Assume $R \ll \omega L$ and $G \ll \omega C$. In this case we have

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:640} \begin{aligned} \gamma &= \sqrt{ (R + j \omega L) ( G + j \omega C ) } \\ &= j \omega \sqrt{L C} \sqrt{ \lr{ 1 + \frac{R}{j\omega L} } \lr{ 1 + \frac{G}{j\omega C} } } \\ &\approx j \omega \sqrt{L C} \lr{ 1 + \frac{R}{2 j\omega L} } \lr{ 1 + \frac{G}{2 j\omega C} } \\ &\approx j \omega \sqrt{L C} \lr{ 1 + \frac{R}{2 j\omega L} + \frac{G}{2 j\omega C} } \\ &= j \omega \sqrt{L C} + j \omega \frac{R \sqrt{C/L}}{2 j\omega} + j \omega \frac{G \sqrt{L/C}}{2 j\omega} \\ &= j \omega \sqrt{L C} + \inv{2} \lr{ R \sqrt{\frac{C}{L}} + G \sqrt{\frac{L}{C}} }, \end{aligned} \end{equation}$$

so
$$\begin{equation}\label{eqn:uwaves4TransmissionLines:660} \begin{aligned} \alpha &= \inv{2} \lr{ R \sqrt{\frac{C}{L}} + G \sqrt{\frac{L}{C}} } \\ \beta &= \omega \sqrt{L C}. \end{aligned} \end{equation}$$

Observe that this value for $\beta$ is the same as the lossless case to first order. We also have

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:680} Z_0 = \sqrt{ \frac{R + j \omega L}{G + j \omega C} } \approx \sqrt{ \frac{L}{C} }, \end{equation}$$

also the same as the lossless case. We must also have $v_\phi = 1/\sqrt{L C}$. To consider a time domain signal note that

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:700} \begin{aligned} V(z) &= V_0^{+} e^{-\gamma z} \\ &= V_0^{+} e^{-\alpha z} e^{-j \beta z}, \end{aligned} \end{equation}$$

so
$$\begin{equation}\label{eqn:uwaves4TransmissionLines:720} \begin{aligned} v(z, t) &= \textrm{Re} \lr{ V(z) e^{j \omega t} } \\ &= \textrm{Re} \lr{ V_0^{+} e^{-\alpha z} e^{-j \beta z} e^{j \omega t} } \\ &= V_0^{+} e^{-\alpha z} \cos( \omega t – \beta z ). \end{aligned} \end{equation}$$

The phase factor can be written

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:740} \omega t – \beta z = \omega \lr{ t – \frac{\beta}{\omega} z } \omega \lr{ t – z/v_\phi }, \end{equation}$$

so the signal still moves with the phase velocity $v_\phi = 1/\sqrt{LC}$, but in a diminishing envelope as sketched in fig. 8.

../../figures/ece1236/deck4TxlineFig8: fig. 8. Time domain envelope for loss loss line.

Notes

• The shape is preserved but the amplitude has an exponential attenuation along the line.
• In this case, since $\beta(\omega)$ is a linear function to first order, we have no dispersion. All of the Fourier components of a pulse travel with the same phase velocity since $v_\phi = \omega/\beta$ is constant. i.e. $v(z, t) = e^{-\alpha z} f( t – z/v_\phi )$. We should expect dispersion when the $R/\omega L$ and $G/\omega C$ start becoming more significant.

Distortionless line.

Motivated by the early telegraphy days, when low loss materials were not available. Therefore lines with a constant attenuation and constant phase velocity (i.e. no dispersion) were required in order to eliminate distortion of the signals. This can be achieved by setting

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:760} \frac{R}{L} = \frac{G}{C}. \end{equation}$$

When that is done we have
$$\begin{equation}\label{eqn:uwaves4TransmissionLines:780} \begin{aligned} \gamma &= \sqrt{ (R + j \omega L) ( G + j \omega C ) } \\ &= j \omega \sqrt{L C} \sqrt{ \lr{ 1 + \frac{R}{j \omega L} } \lr{ 1 + \frac{G}{j \omega C} } } \\ &= j \omega \sqrt{L C} \sqrt{ \lr{ 1 + \frac{R}{j \omega L} } \lr{ 1 + \frac{R}{j \omega L} } } \\ &= j \omega \sqrt{L C} \lr{ 1 + \frac{R}{j \omega L} } \\ &= R \sqrt{\frac{C}{L} } + j \omega \sqrt{L C} \\ &= \sqrt{R G } + j \omega \sqrt{L C}. \end{aligned} \end{equation}$$

We have

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:800} \begin{aligned} \alpha &= \sqrt{R G } \\ \beta &= \omega \sqrt{L C}. \end{aligned} \end{equation}$$

The phase velocity is the same as that of the lossless and low-loss lines

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:820} v_\phi = \frac{\omega}{\beta} = \inv{\sqrt{L C}}. \end{equation}$$

Terminated lossless line.

Consider the load configuration sketched in fig. 9.

../../figures/ece1236/deck4TxlineFig9: fig. 9. Terminated line.

Recall that

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:840} \begin{aligned} V(z) &= V_0^{+} e^{-j \beta z} + V_0^{-} e^{+j \beta z} \\ I(z) &= \frac{V_0^{+}}{Z_0} e^{-j \beta z} – \frac{V_0^{-}}{Z_0} e^{+j \beta z} \\ \end{aligned} \end{equation}$$

At the load ($z = 0$), we have

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:860} \begin{aligned} V(0) &= V_0^{+} + V_0^{-} \\ I(0) &= \inv{Z_0} \lr{ V_0^{+} – V_0^{-} } \end{aligned} \end{equation}$$

So

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:880} \begin{aligned} Z_{\textrm{L}} &= \frac{V(0)}{I(0)} \\ &= Z_0 \frac{ V_0^{+} + V_0^{-} }{ V_0^{+} – V_0^{-} } \\ &= Z_0 \frac{ 1 + \Gamma_{\textrm{L}} }{1 – \Gamma_{\textrm{L}} }, \end{aligned} \end{equation}$$

where

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:900} \Gamma_{\textrm{L}} \equiv \frac{V_0^{-} }{V_0^{+}}, \end{equation}$$

is the reflection coefficient at the load.

The phasors for the signals take the form

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:920} \begin{aligned} V(z) &= V_0^{+} \lr{ e^{-j \beta z} + \Gamma_{\textrm{L}} e^{+j \beta z} } \\ I(z) &= \frac{V_0^{+}}{Z_0} \lr{ e^{-j \beta z} – \Gamma_{\textrm{L}} e^{+j \beta z} }. \end{aligned} \end{equation}$$

Observe that we can rearranging for $\Gamma_{\textrm{L}}$ in terms of the impedances

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:940} \lr{ 1 – \Gamma_{\textrm{L}} } Z_{\textrm{L}} = Z_0 \frac{ 1 + \Gamma_{\textrm{L}} }, \end{equation}$$

or
$$\begin{equation}\label{eqn:uwaves4TransmissionLines:960} \Gamma_{\textrm{L}} \lr{ Z_0 + Z_{\textrm{L}} } = Z_{\textrm{L}} – Z_0, \end{equation}$$

or
$$\begin{equation}\label{eqn:uwaves4TransmissionLines:980} \Gamma_{\textrm{L}} = \frac{Z_{\textrm{L}} – Z_0} { Z_0 + Z_{\textrm{L}} } . \end{equation}$$

Power

The average (time) power on the line is

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:1000} \begin{aligned} P_{ \textrm{av}} &= \inv{2} \textrm{Re}\lr{ V(Z) I^\conj(z) } \\ &= \inv{2} \textrm{Re} \lr{ V_0^{+} \lr{ e^{-j \beta z} + \Gamma_{\textrm{L}} e^{+j \beta z} } \lr{\frac{V_0^{+}}{Z_0}}^\conj \lr{ e^{j \beta z} – \Gamma_{\textrm{L}}^\conj e^{-j \beta z} } } \\ &= \frac{ \Abs{V_0^{+}}^2 }{2 Z_0 } \textrm{Re}\lr{ 1 + \Gamma_{\textrm{L}} e^{2 j \beta z} – \Gamma_{\textrm{L}}^\conj e^{-2 j \beta z} – \Abs{\Gamma_{\textrm{L}}}^2 } \\ &= \frac{ \Abs{V_0^{+}}^2 }{2 Z_0 } \lr{ 1 – \Abs{\Gamma_{\textrm{L}}}^2 }. \end{aligned} \end{equation}$$

where we’ve made use of the fact that $Z_0 = \sqrt{L/C}$ is real for the lossless line, and the fact that a conjugate difference $A – A^\conj = 2 j \textrm{Im}(A)$ is purely imaginary.

This can be written as

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:1020} P_{ \textrm{av}} = P^{+} – P^{-}, \end{equation}$$

where

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:1040} \begin{aligned} P^{+} &= \frac{ \Abs{V_0^{+}}^2 }{2 Z_0 } \\ P^{+} &= \frac{ \Abs{V_0^{+}}^2 }{2 Z_0 } \Abs{\Gamma_{\textrm{L}}}^2. \end{aligned} \end{equation}$$

This difference is the power delivered to the load. This is not z-dependent because we are considering the lossless case. Maximum power is delivered to the load when $\Gamma_{\textrm{L}} = 0$, which occurs when the impedances are matched.

Return loss and insertion loss. Defined.

Return loss (dB) is defined as

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:1060} \begin{aligned} \textrm{RL} &= 10 \log_{10} \frac{P_{\textrm{inc}}}{P_{\textrm{refl}}} \\ &= 10 \log_{10} \inv{\Abs{\Gamma}^2} \\ &= -20 \log_{10} \Abs{\Gamma}. \end{aligned} \end{equation}$$

Insertion loss (dB) is defined as

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:1080} \begin{aligned} \textrm{IL} &= 10 \log_{10} \frac{P_{\textrm{inc}}}{P_{\textrm{trans}}} \\ &= 10 \log_{10} \frac{P^{+}}{P^{+} – P^{-}} \\ &= 10 \log_{10} \inv{1 – \Abs{\Gamma}^2} \\ &= -10 \log_{10} \lr{ 1 – \Abs{\Gamma}^2 }. \end{aligned} \end{equation}$$

Standing wave ratio

Consider again the lossless loaded configuration of fig. 9. Now let $z = – l$, where $l$ is the distance from the load. The phasors at this point on the line are

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:1100} \begin{aligned} V(-l) &= V_0^{+} \lr{ e^{j \beta l} + \Gamma_{\textrm{L}} e^{-j \beta l} } \\ I(-l) &= \frac{V_0^{+}}{Z_0} \lr{ e^{j \beta l} – \Gamma_{\textrm{L}} e^{-j \beta l} } \\ \end{aligned} \end{equation}$$

The absolute voltage at this point is
$$\begin{equation}\label{eqn:uwaves4TransmissionLines:1120} \begin{aligned} \Abs{V(-l)} &= \Abs{V_0^{+}} \Abs{ e^{j \beta l} + \Gamma_{\textrm{L}} e^{-j \beta l} } \\ &= \Abs{V_0^{+}} \Abs{ 1 + \Gamma_{\textrm{L}} e^{-2 j \beta l} } \\ &= \Abs{V_0^{+}} \Abs{ 1 + \Abs{\Gamma_{\textrm{L}}} e^{j \Theta_{\textrm{L}}} e^{-2 j \beta l} }, \end{aligned} \end{equation}$$

where the complex valued $\Gamma_{\textrm{L}}$ is given by $\Gamma_{\textrm{L}} = \Abs{\Gamma_{\textrm{L}}} e^{j \Theta_{\textrm{L}}}$.

This gives
$$\begin{equation}\label{eqn:uwaves4TransmissionLines:1140} \Abs{V(-l)} = \Abs{V_0^{+}} \Abs{ 1 + \Abs{\Gamma_{\textrm{L}}} e^{j(\Theta_{\textrm{L}} -2 \beta l)} }. \end{equation}$$

The voltage magnitude oscillates as one moves along the line. The maximum occurs when $e^{j (\Theta_{\textrm{L}} -2 \beta l)} = 1$

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:1160} V_{\mathrm{max}} = \Abs{V_0^{+}} \Abs{ 1 + \Abs{\Gamma_{\textrm{L}}} }. \end{equation}$$

This occurs when $\Theta_{\textrm{L}} – 2 \beta l = 2 k \pi$ for $k = 0, 1, 2, \cdots$. The minimum occurs when $e^{j (\Theta_{\textrm{L}} -2 \beta l)} = -1$

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:1180} V_{\mathrm{min}} = \Abs{V_0^{+}} \Abs{ 1 – \Abs{\Gamma_{\textrm{L}}} }, \end{equation}$$

which occurs when $\Theta_{\textrm{L}} – 2 \beta l = (2 k – 1 )\pi$ for $k = 1, 2, \cdots$. The standing wave ratio is defined as

$$\begin{equation}\label{eqn:uwaves4TransmissionLines:1200} \textrm{SWR} = \frac{V_{\mathrm{max}}}{V_{\mathrm{min}}} = \frac{ 1 + \Abs{\Gamma_{\textrm{L}}} }{ 1 – \Abs{\Gamma_{\textrm{L}}} }. \end{equation}$$

This is a measure of the mismatch of a line. This is sketched in fig. 10.

../../figures/ece1236/deck4TxlineFig10: fig. 10. SWR extremes.

Notes:

• Since $0 \le \Abs{\Gamma_{\textrm{L}}} \le 1$, we have $1 \le \textrm{SWR} \le \infty$. The lower bound is for a matched line, and open, short, or purely reactive termination leads to the infinities.
• The distance between two successive maxima (or minima) can be determined by setting $\Theta_{\textrm{L}} – 2 \beta l = 2 k \pi$ for two consecutive values of $k$. For $k = 0$, suppose that $V_{\mathrm{max}}$ occurs at $d_1$

  $$\begin{equation}\label{eqn:uwaves4TransmissionLines:1220} \Theta_{\textrm{L}} – 2 \beta d_1 = 2 (0) \pi, \end{equation}$$

  or
  $$\begin{equation}\label{eqn:uwaves4TransmissionLines:1240} d_1 = \frac{\Theta_{\textrm{L}}}{2 \beta}. \end{equation}$$

  For $k = 1$, let the max occur at $d_2$

  $$\begin{equation}\label{eqn:uwaves4TransmissionLines:1260} \Theta_{\textrm{L}} – 2 \beta d_2 = 2 (1) \pi, \end{equation}$$

  or
  $$\begin{equation}\label{eqn:uwaves4TransmissionLines:1280} d_2 = \frac{\Theta_{\textrm{L}} – 2 \pi}{2 \beta}. \end{equation}$$

  The difference is

  $$\begin{equation}\label{eqn:uwaves4TransmissionLines:1300} \begin{aligned} d_1 – d_2 &= \frac{\Theta_{\textrm{L}}}{2 \beta} – \frac{\Theta_{\textrm{L}} – 2 \pi}{2 \beta} \\ &= \frac{\pi}{\beta} \\ &= \frac{\pi}{2 \pi/\lambda} \\ &= \frac{\lambda}{2}. \end{aligned} \end{equation}$$

  The distance between two consecutive maxima (or minima) of the SWR is $\lambda/2$.

Impedance Transformation.

Referring to fig. 11, let’s solve for the impedance at the load where $z = 0$ and at $z = -l$.

../../figures/ece1236/deck4TxlineFig11: fig. 11. Configuration for impedance transformation.

At any point on the line we have

$$\begin{equation}\label{eqn:uwaves4TransmissionLinesCore:1320} V(z) = V_0^{+} e^{-j \beta z} \lr{ 1 + \Gamma_{\textrm{L}} e^{2 j \beta z} }, \end{equation}$$

so at the load and input we have

$$\begin{equation}\label{eqn:uwaves4TransmissionLinesCore:1340} \begin{aligned} V_{\textrm{L}} &= V_0^{+} \lr{ 1 + \Gamma_{\textrm{L}} } \\ V(-l) &= V^{+} \lr{ 1 + \Gamma_{\textrm{L}}(-1) }, \end{aligned} \end{equation}$$

where

$$\begin{equation}\label{eqn:uwaves4TransmissionLinesCore:1360} \begin{aligned} V^{+} &= V_0^{+} e^{ j \beta l } \\ \Gamma_{\textrm{L}}(-1) &= \Gamma_{\textrm{L}} e^{-2 j \beta l} \end{aligned} \end{equation}$$

Similarly

$$\begin{equation}\label{eqn:uwaves4TransmissionLinesCore:1380} I(-l) = \frac{V^{+}}{Z_0} \lr{ 1 – \Gamma_{\textrm{L}}(-1) }. \end{equation}$$

Define an input impedance as
$$\begin{equation}\label{eqn:uwaves4TransmissionLinesCore:1400} \begin{aligned} Z_{\textrm{in}} &= \frac{V(-l)}{I(-l)} \\ &= Z_0 \frac{1 + \Gamma_{\textrm{L}}(-1)}{1 – \Gamma_{\textrm{L}}(-1)} \end{aligned} \end{equation}$$

This is analogous to

$$\begin{equation}\label{eqn:uwaves4TransmissionLinesCore:1420} Z_{\textrm{L}} = Z_0 \frac{1 + \Gamma_{\textrm{L}}}{1 – \Gamma_{\textrm{L}}} \end{equation}$$

From $\ref{eqn:uwaves4TransmissionLines:980}$, we have

$$\begin{equation}\label{eqn:uwaves4TransmissionLinesCore:1440} \begin{aligned} Z_{\textrm{in}} &= Z_0 \frac{Z_0 + Z_{\textrm{L}} + \lr{Z_{\textrm{L}} – Z_0} e^{-2 j \beta l}}{Z_0 + Z_{\textrm{L}} – \lr{Z_{\textrm{L}} – Z_0} e^{-2 j \beta l}} \\ &= Z_0 \frac{\lr{Z_0 + Z_{\textrm{L}}} e^{j\beta l} + \lr{Z_{\textrm{L}} – Z_0} e^{- j \beta l}}{\lr{Z_0 + Z_{\textrm{L}}} e^{j\beta l} – \lr{Z_{\textrm{L}} – Z_0} e^{- j \beta l}} \\ &= Z_0 \frac {Z_{\textrm{L}} \cos( \beta l ) + j Z_0 \sin(\beta l ) } {Z_0 \cos( \beta l ) + j Z_{\textrm{L}} \sin(\beta l ) }, \end{aligned} \end{equation}$$

or
$$\begin{equation}\label{eqn:uwaves4TransmissionLinesCore:1460} \boxed{ Z_{\textrm{in}} = \frac {Z_{\textrm{L}} + j Z_0 \tan(\beta l ) } {Z_0 + j Z_{\textrm{L}} \tan(\beta l ) }. } \end{equation}$$

This can be thought of as providing a reflection coefficient function along the line to the load at any point as sketched in fig. 12.

../../figures/ece1236/deck4TxlineFig12: fig. 12. Impedance transformation reflection on the line.

References

[1] David M Pozar. Microwave engineering. John Wiley \& Sons, 2009.