September 29, 2018 phy2403
Working on a problem from Peskin and Schroeder (and Zee too actually), I’ve hit dead ends in many different ways. The last dead end looks impressive just sitting there on the table where I abandoned it:
… however, after getting results that weren’t expected a number of different ways, I think I finally understand the fundamental assumption that I had wrong. Take >= IV.
September 28, 2018 Incoherent ramblings identity politics, rant, york region district school board
York region district school board is preparing to roll out their “Every Student Counts Survey” for primary grades (to be answered with parental assistance) or by oneself in grade 7-12 that’s packed full of the extreme identity politics that is discussed so widely in podcasts these days.
Here’s a link to a sample copy of the survey for kindergarden to grade 6, and one for higher grades. The one for the little kids is particularly absurd, asking the kids or parents to pick from gender identities of male, female or one of the following 7 additional options:
as constrained by the footnote: “A person’s internal and deeply felt sense of being a man, a woman, both, neither, or having another identity on the gender spectrum. A person’s gender identity may be different from the sex assigned at birth (for example, female, intersex, male).”
These are questions being asked of kids that are potentially still many years away from puberty! Why on earth is there such pressure to have the kids pick from or even try to understand these host of made up categories?
When I was in grade 7 I got teased about being gay because I was too shy to ask a girl on a date (or accept a date, in one instance). Heck, I was a virgin until I was in my early twenties. If this level of gender propaganda was being pushed when I was a kid, I’d have to have started wearing a lipstick and blouses just to fit it. All because I was introverted and shy. My sexual identity had nothing to do with these plethora of current gender categories, but just because I hadn’t clued in that you had to communicate to the opposite sex if you wanted to make any progress towards sexual goals. Time is required to figure this stuff out, and having to choose prematurely, seems, to be blunt, completely stupid.
There’s some other stuff in this survey that is just bizarre. The desire to label is so severe that it appears they are also making up new races:
Latino/Latina/Latinx
Googling Latinx, which I hadn’t heard of, and isn’t defined in any of the “helpful” footnotes, it appears that they are pushing gender politics into race too. Wikipedia says of this: “Latinx (la-teen-ex) is a gender-neutral term sometimes used in lieu of Latino or Latina”.
Here’s some samples of the gobbledegook that this survey is packed full of:
I wonder how much money York region is paying to roll out and process this survey? As well as injecting chaos and insanity into the school system in liew of actual content, it seems like a pointless waste of time and money that will provide little useful information.
If you want to make progress in education, how about stripping out some of the crap. There’s no shortage of that. Let’s not confuse kids with four different pictoral multiplication algorithms, so that they’ll give up and end up using calculators. How about not injecting terminology into math education like “commutative” in grade 5 when you won’t see non-commutative (i.e. matrix) multiplication until university (since linear algebra seems to have been dropped from the high school curriculum for all intents and purposes). Arg!
September 26, 2018 phy2403 annillation operator, Canonical quantization, creation operator, Harmonic oscillator
[Click here for a PDF of this post with nicer formatting]
These are notes for the UofT course PHY2403H, Quantum Field Theory I, taught by Prof. Erich Poppitz fall 2018.
We are engaging in the “canonical” or Hamiltonian method of quantization. It is also possible to quantize using path integrals, but it is hard to prove that operators are unitary doing so. In fact, the mechanism used to show unitarity from path integrals is often to find the Lagrangian and show that there is a Hilbert space (i.e. using canonical quantization). Canonical quantization essentially demands that the fields obey a commutator relation of the following form
\begin{equation}\label{eqn:qftLecture6:20}
\antisymmetric{\pi(\Bx, t)}{\phi(\By, t)} = -i \delta^3(\Bx – \By).
\end{equation}
We assumed that the quantized fields obey the Hamiltonian relations
\begin{equation}\label{eqn:qftLecture6:160}
\begin{aligned}
\ddt{\phi} &= i \antisymmetric{H}{\phi} \\
\ddt{\pi} &= i \antisymmetric{H}{\pi}.
\end{aligned}
\end{equation}
We were working with the Hamiltonian density
\begin{equation}\label{eqn:qftLecture6:40}
\mathcal{H} =
\inv{2} (\pi(\Bx, t))^2
+
\inv{2} (\spacegrad \phi(\Bx, t))^2
+
\frac{m^2}{2} \phi^2
+
\frac{\lambda}{4} \phi^4,
\end{equation}
which included a mass term \( m \) and a potential term (\(\lambda\)). We will expand all quantities in Taylor series in \( \lambda \) assuming they have a structure such as
\begin{equation}\label{eqn:qftLecture6:180}
\begin{aligned}
f(\lambda) =
c_0 \lambda^0
+ c_1 \lambda^1
+ c_2 \lambda^2
+ c_3 \lambda^3
+ \cdots
\end{aligned}
\end{equation}
We will stop this \underline{perturbation theory} approach at \( O(\lambda^2) \), and will ignore functions such as \( e^{-1/\lambda} \).
Within perturbation theory, to leaving order, set \( \lambda = 0 \), so that \( \phi \) obeys the Klein-Gordon equation (if \( m = 0 \) we have just a d’Lambertian (wave equation)).
We can write our field as a Fourier transform
\begin{equation}\label{eqn:qftLecture6:60}
\phi(\Bx, t) = \int \frac{d^3 p}{(2\pi)^3} e^{i \Bp \cdot \Bx} \tilde{\phi}(\Bp, t),
\end{equation}
and due to a Hermitian assumption (i.e. real field) this implies
\begin{equation}\label{eqn:qftLecture6:80}
\tilde{\phi}^\conj(\Bp, t) = \tilde{\phi}(-\Bp, t).
\end{equation}
We found that the Klein-Gordon equation implied that the momentum space representation obey Harmonic oscillator equations
\begin{equation}\label{eqn:qftLecture6:100}
\begin{aligned}
\ddot{\tilde{\phi}}(\Bp, t) &= – \omega_\Bp \tilde{\phi}(\Bp, t) \\
\omega_\Bp &= \sqrt{\Bp^2 + m^2}.
\end{aligned}
\end{equation}
We may represent the solution to this equation as
\begin{equation}\label{eqn:qftLecture6:120}
\tilde{\phi}(\Bq, t) = \inv{\sqrt{2 \omega_\Bq}} \lr{
e^{-i \omega_\Bq t} a_\Bq
+
e^{i \omega_\Bq t} b_\Bq^\conj
}.
\end{equation}
This is a general solution, but imposing \( a_\Bq = b_{-\Bq} \) ensures \ref{eqn:qftLecture6:80} is satisfied.
This leaves us with
\begin{equation}\label{eqn:qftLecture6:140}
\tilde{\phi}(\Bq, t) = \inv{\sqrt{2 \omega_\Bq}} \lr{
e^{-i \omega_\Bq t} a_\Bq
+
e^{i \omega_\Bq t} a_{-\Bq}^\conj
}.
\end{equation}
We want to show that iff
\begin{equation}\label{eqn:qftLecture6:200}
\antisymmetric{a_\Bq}{a^\dagger_\Bp} = \lr{ 2 \pi }^3 \delta^3(\Bp – \Bq),
\end{equation}
then
\begin{equation}\label{eqn:qftLecture6:220}
\antisymmetric{\pi(\By, t)}{\phi(\Bx, t)} = -i \delta^3(\Bx – \By)
\end{equation}
where everything else commutes (i.e. \(
\antisymmetric{a_\Bp}{a_\Bq} =
\antisymmetric{a_\Bp^\dagger}{a_\Bq^\dagger} = 0 \)).
We will only show one direction, but you can go the other way too.
\begin{equation}\label{eqn:qftLecture6:240}
\phi(\Bx, t)
=
\int \frac{d^3 p}{(2\pi)^3 \sqrt{2 \omega_\Bp}} e^{i \Bp \cdot \Bx}
\lr{
e^{-i \omega_\Bp t} a_\Bp
+
e^{i \omega_\Bp t} a_{-\Bp}^\dagger
}
\end{equation}
\begin{equation}\label{eqn:qftLecture6:260}
\pi(\Bx, t) = \dot{\phi}
=
i \int \frac{d^3 q}{(2\pi)^3 \sqrt{2 \omega_\Bq}} \omega_\Bq e^{i \Bq \cdot \Bx}
\lr{
-e^{-i \omega_\Bq t} a_\Bq
+
e^{i \omega_\Bq t} a_{-\Bq}^\dagger
}
\end{equation}
The commutator is
\begin{equation}\label{eqn:qftLecture6:280}
\begin{aligned}
\antisymmetric{\pi(\By, t)}{\phi(\Bx, t)}
&=
i \int \frac{d^3 p}{(2\pi)^3
\sqrt{2 \omega_\Bp}}
\frac{d^3 q}{(2\pi)^3 \sqrt{2 \omega_\Bq}}
\omega_\Bq
e^{i \Bp \cdot \By + i \Bq \cdot \Bx}
\antisymmetric
{
-e^{-i \omega_\Bq t} a_\Bq
+
e^{i \omega_\Bq t} a_{-\Bq}^\dagger
}
{
e^{-i \omega_\Bp t} a_\Bp
+
e^{i \omega_\Bp t} a_{-\Bp}^\dagger
} \\
&=
i \int \frac{d^3 p}{(2\pi)^3
\sqrt{2 \omega_\Bp}}
\frac{d^3 q}{(2\pi)^3 \sqrt{2 \omega_\Bq}}
\omega_\Bq
e^{i \Bp \cdot \By + i \Bq \cdot \Bx}
\lr{
– e^{i (\omega_\Bp -\omega_\Bq) t}
\antisymmetric { a_\Bq } { a_{-\Bp}^\dagger }
+
e^{i (\omega_\Bq -\omega_\Bp) t}
\antisymmetric{a_{-\Bq}^\dagger}{ a_\Bp }
} \\
&=
i \int \frac{d^3 p}{(2\pi)^3
\sqrt{2 \omega_\Bp}}
\frac{d^3 q}{(2\pi)^3 \sqrt{2 \omega_\Bq}}
\omega_\Bq (2\pi)^3
e^{i \Bp \cdot \By + i \Bq \cdot \Bx}
\lr{
– e^{i (\omega_\Bp -\omega_\Bq) t} \delta^3(\Bq + \Bp)
– e^{i (\omega_\Bq -\omega_\Bp) t} \delta^3(-\Bq -\Bp)
} \\
&=
– 2 i \int \frac{d^3 p}{(2\pi)^3
2 \omega_\Bp}
\omega_\Bp
e^{i \Bp \cdot (\By – \Bx)} \\
&=
-i \delta^3(\By – \Bx),
\end{aligned}
\end{equation}
which is what we wanted to prove.
We call the \( \lambda = 0 \) case the “free” Hamiltonian.
\begin{equation}\label{eqn:qftLecture6:300}
\begin{aligned}
H
&= \int d^3 x \lr{ \inv{2} \pi^2 + \inv{2} (\spacegrad \phi)^2 + \frac{m^2}{2} \phi^2 } \\
&=
\inv{2} \int d^3 x
\frac{d^3 p}{(2\pi)^3}
\frac{d^3 q}{(2\pi)^3}
\frac{
e^{i (\Bp + \Bq)\cdot \Bx}
}{\sqrt{2 \omega_\Bp}
\sqrt{2 \omega_\Bq}}
\lr{
–
(\omega_\Bp)
(\omega_\Bq)
\lr{
-e^{-i \omega_\Bp t} a_\Bp
+
e^{i \omega_\Bp t} a_{-\Bp}^\dagger
}
\lr{
-e^{-i \omega_\Bq t} a_\Bq
+
e^{i \omega_\Bq t} a_{-\Bq}^\dagger
}
}
–
\Bp \cdot \Bq
\lr{
e^{-i \omega_\Bp t} a_\Bp
+
e^{i \omega_\Bp t} a_{-\Bp}^\dagger
}
\lr{
e^{-i \omega_\Bq t} a_\Bq
+
e^{i \omega_\Bq t} a_{-\Bq}^\dagger
}
+
m^2
\lr{
e^{-i \omega_\Bp t} a_\Bp
+
e^{i \omega_\Bp t} a_{-\Bp}^\dagger
}
\lr{
e^{-i \omega_\Bq t} a_\Bq
+
e^{i \omega_\Bq t} a_{-\Bq}^\dagger
}.
\end{aligned}
\end{equation}
An immediate simplification is possible by identifying a delta function factor \( \int d^3 x e^{i(\Bp + \Bq) \cdot \Bx}/(2\pi)^3 = \delta^3(\Bp + \Bq) \), so
\begin{equation}\label{eqn:qftLecture6:1060}
\begin{aligned}
H
&=
\inv{2}
\int
\frac{d^3 p}{(2\pi)^3}
\frac{1
}{2 \omega_\Bp}
\lr{
–
(\omega_\Bp)^2
\lr{
-e^{-i \omega_\Bp t} a_\Bp
+
e^{i \omega_\Bp t} a_{-\Bp}^\dagger
}
\lr{
-e^{-i \omega_\Bp t} a_{-\Bp}
+
e^{i \omega_\Bp t} a_{\Bp}^\dagger
}
}
+
(\Bp^2 + m^2)
\lr{
e^{-i \omega_\Bp t} a_\Bp
+
e^{i \omega_\Bp t} a_{-\Bp}^\dagger
}
\lr{
e^{-i \omega_\Bp t} a_{-\Bp}
+
e^{i \omega_\Bp t} a_{\Bp}^\dagger
} \\
&=
\inv{2} \int \frac{d^3 p}{(2 \pi)^3} \inv{2 \omega_\Bp}
\lr{
a_\Bp a_{-\Bp}
\lr{
{-\omega_\Bp^2 e^{-2 i \omega_\Bp t}}
+
{\omega_\Bp^2 e^{-2 i \omega_\Bp t}}
}
+
a_{-\Bp}^\dagger a_{\Bp}^\dagger
\lr{
-{\omega_\Bp^2 e^{2 i \omega_\Bp t}}
+
{\omega_\Bp^2 e^{2 i \omega_\Bp t}}
}
+
a_\Bp a^\dagger_{\Bp} \omega^2_\Bp(1 + 1)
+
a^\dagger_{-\Bp} a_{-\Bp} \omega^2_\Bp(1 + 1)
}
\end{aligned}
\end{equation}
When all is said and done we are left with
\begin{equation}\label{eqn:qftLecture6:320}
H =
\int \frac{d^3 p}{(2 \pi)^3} \frac{\omega_\Bp}{2} \lr{
a^\dagger_{-\Bp}
a_{-\Bp}
+
a_{\Bp}
a^\dagger_{\Bp}
}
\end{equation}
and finally with a \( \Bp \rightarrow -\Bp \) transformation (\( \iiint_{-R}^R d^3 p \rightarrow (-1)^3 \iiint_R^{-R} d^3 p’ = (-1)^6 \iiint_{-R}^R d^3 p’ \)) in the first integral our free Hamiltonian (\( \lambda = 0 \)) is
\begin{equation}\label{eqn:qftLecture6:340}
\boxed{
H_0 =
\int \frac{d^3 p}{(2 \pi)^3} \frac{\omega_\Bp}{2} \lr{
a^\dagger_{\Bp}
a_{\Bp}
+
a_{\Bp}
a^\dagger_{\Bp}
}
}
\end{equation}
From the commutator relationship \ref{eqn:qftLecture6:200} we can write
\begin{equation}\label{eqn:qftLecture6:360}
a_\Bp a^\dagger_\Bq
=
a^\dagger_\Bq
a_\Bp
+ (2 \pi)^3 \delta^3(\Bp – \Bq),
\end{equation}
so
\begin{equation}\label{eqn:qftLecture6:380}
H_0 =
\int \frac{d^3 p}{(2 \pi)^3} \omega_\Bp
\lr{
a^\dagger_{\Bp}
a_{\Bp}
+
\inv{2} (2 \pi)^3 \delta^3(0)
}
\end{equation}
The delta function term can be interpreted using
\begin{equation}\label{eqn:qftLecture6:400}
(2 \pi)^3 \delta^3(\Bq)
= \int d^3 x e^{i \Bq \cdot \Bx},
\end{equation}
so when \( \Bq = 0 \)
\begin{equation}\label{eqn:qftLecture6:420}
(2 \pi)^3 \delta^3(0) = \int d^3 x = V.
\end{equation}
We can write the Hamiltonian now in terms of the volume
\begin{equation}\label{eqn:qftLecture6:440}
\boxed{
H_0 =
\int \frac{d^3 p}{(2 \pi)^3} \omega_\Bp
a^\dagger_{\Bp}
a_{\Bp}
+ V_3
\int \frac{d^3 p}{(2 \pi)^3} \frac{\omega_\Bp }{2} \times 1
}
\end{equation}
In units with \( m = 1 \) the non-relativistic QM SHO has the Hamiltonian
\begin{equation}\label{eqn:qftLecture6:460}
H
= \inv{2} p^2 + \frac{\omega^2}{2} q^2.
\end{equation}
If we define a position operator with a time-domain Fourier representation given by
\begin{equation}\label{eqn:qftLecture6:480}
q = \inv{\sqrt{2\omega}} \lr{ a e^{-i \omega t} + a^\dagger e^{i \omega t} },
\end{equation}
where the Fourier coefficients \( a, a^\dagger \) are operator valued, then the momentum operator is
\begin{equation}\label{eqn:qftLecture6:500}
p = \dot{q} =
\frac{i\omega}{\sqrt{2\omega}} \lr{ -a e^{-i \omega t} + a^\dagger e^{i \omega t} },
\end{equation}
or inverting for \( a, a^\dagger \)
\begin{equation}\label{eqn:qftLecture6:1080}
\begin{aligned}
a &= \sqrt{\frac{\omega}{2}} \lr{ q – \inv{i \omega} p } e^{-i \omega t} \\
a^\dagger &= \sqrt{\frac{\omega}{2}} \lr{ q + \inv{i \omega} p } e^{i \omega t}.
\end{aligned}
\end{equation}
By inspection it is apparent that the product \( a^\dagger a \) will be related to the Hamiltonian (i.e. a difference of squares). That product is
\begin{equation}\label{eqn:qftLecture6:1120}
\begin{aligned}
a^\dagger a
&=
\frac{\omega}{2}
\lr{ q + \inv{i \omega} p }
\lr{ q – \inv{i \omega} p } \\
&=
\frac{\omega}{2} \lr{ q^2 + \inv{\omega^2} p^2 – \inv{i \omega} \antisymmetric{q}{p} } \\
&= \inv{2 \omega} \lr{ p^2 + \omega^2 q^2 – \omega },
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:qftLecture6:1140}
H = \omega \lr{ a^\dagger a + \inv{2} }.
\end{equation}
We can glean some of the properties of \( a, a^\dagger \) by computing the commutator of \( p, q \), since that has a well known value
\begin{equation}\label{eqn:qftLecture6:520}
\begin{aligned}
i
&= \antisymmetric{q}{p} \\
&=
\frac{i\omega}{2 \omega} \antisymmetric
{ a e^{-i \omega t} + a^\dagger e^{i \omega t} }
{ -a e^{-i \omega t} + a^\dagger e^{i \omega t} } \\
&=
\frac{i}{2} \lr{
\antisymmetric{a}{a^\dagger} –
\antisymmetric{a^\dagger}{a} } \\
&=
i
\antisymmetric{a}{a^\dagger},
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:qftLecture6:1100}
\antisymmetric{a}{a^\dagger} = 1.
\end{equation}
The operator \( a^\dagger a \) is the workhorse of the Hamiltonian and worth studying independently. In particular, assume that we have a set of states \( \ket{n} \) that are eigenstates of \( a^\dagger a \) with eigenvalues \( \lambda_n \), that is
\begin{equation}\label{eqn:qftLecture6:1160}
a^\dagger a \ket{n} = \lambda_n \ket{n}.
\end{equation}
The action of \( a^\dagger a \) on \( a^\dagger \ket{n} \) is easy to compute
\begin{equation}\label{eqn:qftLecture6:1180}
\begin{aligned}
a^\dagger a a^\dagger \ket{n}
&=
a^\dagger \lr{ a^\dagger a + 1 } \ket{n} \\
&=
\lr{ \lambda_n + 1 } a^\dagger \ket{n},
\end{aligned}
\end{equation}
so \( \lambda_n + 1 \) is an eigenvalue of \( a^\dagger \ket{n} \). The state \( a^\dagger \ket{n} \) has an energy eigenstate that is one unit of energy larger than \( \ket{n} \). For this reason we called \( a^\dagger \) the raising (or creation) operator.
Similarly,
\begin{equation}\label{eqn:qftLecture6:1200}
\begin{aligned}
a^\dagger a a \ket{n}
&=
\lr{ a a^\dagger – 1 } a \ket{n} \\
&=
(\lambda_n – 1) a \ket{n},
\end{aligned}
\end{equation}
so \( \lambda_n – 1 \) is the energy eigenvalue of \( a \ket{n} \), having one less unit of energy than \( \ket{n} \).
We call \( a \) the annihilation (or lowering) operator.
If we argue that there is a lowest energy state, perhaps designated as \( \ket{0} \) then we must have
\begin{equation}\label{eqn:qftLecture6:560}
a\ket{0} = 0,
\end{equation}
by the assumption that there are no energy eigenstates with less energy than \( \ket{0} \).
We can think of higher order states being constructed from the ground state from using the raising operator \( a^\dagger \)
\begin{equation}\label{eqn:qftLecture6:580}
\ket{n} = \frac{(a^\dagger)^n}{\sqrt{n!}} \ket{0}
\end{equation}
We’ve diagonalized in the Fourier representation for the momentum space fields. For every value of momentum \( \Bp \) we have a quantum SHO.
For our field space we call our space the Fock vacuum and
\begin{equation}\label{eqn:qftLecture6:620}
a_\Bp\ket{0} = 0,
\end{equation}
and call \( a_\Bp \) the “annihilation operator”, and
call \( a^\dagger_\Bp \) the “creation operator”.
We say that \( a^\dagger_\Bp \ket{0} \) is the creation of a state of a single particle of momentum \( \Bp \) by \( a^\dagger_\Bp \).
We are discarding the volume term, a procedure called “normal ordering”. We define
\begin{equation}\label{eqn:qftLecture6:640}
\frac{a^\dagger a + a a^\dagger}{2}
:\equiv
a^\dagger a
\end{equation}
We are essentially forgetting the vacuum energy as some sort of unobservable quantity, leaving us with the free Hamiltonian of
\begin{equation}\label{eqn:qftLecture6:660}
H_0 =
\int \frac{d^3 p}{(2 \pi)^3} \omega_\Bp
a^\dagger_{\Bp}
a_{\Bp}
\end{equation}
Consider
\begin{equation}\label{eqn:qftLecture6:680}
\begin{aligned}
H_0
a^\dagger_\Bq \ket{0}
&=
\int \frac{d^3 p}{(2 \pi)^3} \omega_\Bp
a^\dagger_{\Bp}
a_{\Bp}
a^\dagger_\Bq
\ket{0} \\
&=
\int \frac{d^3 p}{(2 \pi)^3} \omega_\Bp
a^\dagger_{\Bp}
\lr{
a^\dagger_\Bq a_\Bp + (2 \pi)^3 \delta^3(\Bp – \Bq)
}
\ket{0} \\
&=
\int \frac{d^3 p}{(2 \pi)^3} \omega_\Bp
a^\dagger_{\Bp} \lr{
a^\dagger_\Bq {a_\Bp \ket{0}}
+ (2 \pi)^3 \delta^3(\Bp – \Bq) \ket{0}
} \\
&=
\omega_\Bq a^\dagger_\Bq \ket{0}.
\end{aligned}
\end{equation}
Is it possible to modify the Lagrangian or Hamiltonian that we start with so that this vacuum ground state is eliminated? Answer: Only by imposing super-symmetric constraints (that pairs this (Bosonic) Hamiltonian to a Fermonic system in a way that there is exact cancellation).
We will see that the momentum operator has the form
\begin{equation}\label{eqn:qftLecture6:700}
\mathcal{P}
=
\int \frac{d^3 p}{(2 \pi)^3} \Bp a^\dagger_\Bp a_\Bp.
\end{equation}
We say that \( a^\dagger_\Bp a^\dagger_\Bq \ket{0} \) a two particle space with energy \( \omega_\Bp + \omega_q\), and \(
(a^\dagger_\Bp)^m (a^\dagger_\Bq)^n \ket{0} \equiv
(a^\dagger_\Bp)^m \ket{0} \otimes (a^\dagger_\Bq)^n \ket{0} \), a \( m + n \) particle space.
There is a connection to statistical mechanics that is of interest
\begin{equation}\label{eqn:qftLecture6:720}
\begin{aligned}
\expectation{E}
&= \inv{Z} \sum_n E_n e^{-E_n/\kB T} \\
&= \inv{Z} \sum_n \bra{n} e^{-\hat{H}/\kB T} \hat{H} \ket{n},
\end{aligned}
\end{equation}
so for a SHO Hamiltonian system
\begin{equation}\label{eqn:qftLecture6:740}
\begin{aligned}
\expectation{E}
&= \inv{Z} \sum_n e^{-E_n/\kB T} \bra{n} \hat{H} \ket{n} \\
&= \inv{Z} \sum_n e^{-E_n/\kB T} \bra{n} \omega a^\dagger a \ket{n} \\
&= \frac{\omega}{e^{\omega/\kB T} – 1 } \\ \\
&= \expectation{ \omega a^\dagger a }_{\kB T}
\end{aligned}
\end{equation}
the \( \kB T \) ensemble average energy for a SHO system. Note that this sum was evaluated by noting that \( \bra{n} a^\dagger a \ket{n} = n \) which leaves sums of the form
\begin{equation}\label{eqn:qftLecture6:1220}
\begin{aligned}
\frac{\sum_{n = 0}^\infty n a^n }{\sum_{n = 0}^\infty a^n}
&=
a \frac{\sum_{n = 1}^\infty n a^{n-1} }{\sum_{n = 0}^\infty a^n} \\
&=
a (1 – a) \frac{d}{da} \lr{ \inv{1 – a} } \\
&=
\frac{a}{1 – a}.
\end{aligned}
\end{equation}
If we consider a real scalar field of mass \( m \) we have \( \omega_\Bp = \sqrt{ \Bp^2 + m^2 } \), but for a Maxwell field \( \BE, \BB \) where \( m = 0 \), our dispersion relation is \( \omega_\Bp = \Abs{\Bp} \).
We will see that for a free Maxwell field (no charges or currents) the Hamiltonian is
\begin{equation}\label{eqn:qftLecture6:760}
H_{\text{Maxwell}} =
\sum_{i = 1}^2
\int \frac{d^3 p}{(2 \pi)^3} \omega_\Bp {a^i}^\dagger_\Bp {a^i}_\Bp,
\end{equation}
where \( i \) is a polarization index.
We expect that we can evaluate an average such as \ref{eqn:qftLecture6:740} for our field, and operate using the analogy
\begin{equation}\label{eqn:qftLecture6:780}
\begin{aligned}
a a^\dagger &= a^\dagger a + 1 \\
a_\Bp a_\Bp^\dagger &= a_\Bp^\dagger a_\Bp + V_3.
\end{aligned}
\end{equation}
so if we rescale by \( \sqrt{V_3} \)
\begin{equation}\label{eqn:qftLecture6:800}
a_\Bp = \sqrt{V_3} \tilde{a}_\Bp
\end{equation}
Then we have commutator relations like standard QM
\begin{equation}\label{eqn:qftLecture6:820}
\tilde{a} \tilde{a}^\dagger = \tilde{a}^\dagger \tilde{a} + 1.
\end{equation}
So we can immediately evaluate the energy expectation for our quantized fields
\begin{equation}\label{eqn:qftLecture6:840}
\begin{aligned}
\expectation{H_0}
&=
\expectation{
\int \frac{d^3 p}{(2 \pi)^3} \omega_\Bp a_\Bp^\dagger a_\Bp
} \\
&=
\int \frac{d^3 p}{(2 \pi)^3} \omega_\Bp V_3 \expectation{ \tilde{a}^\dagger_\Bp a_\Bp } \\
&=
V_3
\int \frac{d^3 p}{(2 \pi)^3} \frac{\omega_\Bp}{e^{\omega_\Bp/\kB T} – 1}.
\end{aligned}
\end{equation}
Using this with the Maxwell field, we have a factor of two from polarization
\begin{equation}\label{eqn:qftLecture6:860}
U^{\text{Maxwell}} = 2 V_3
\int \frac{d^3 p}{(2 \pi)^3} \frac{\Abs{\Bp}}{e^{\omega_\Bp/\kB T} – 1},
\end{equation}
which is Planck’s law describing the blackbody energy spectrum.
The question is how to apply the CCR results to moving frames, which is done using Lorentz transformations. Just like we know that the exponential of the Hamiltonian (times time) represents time translations, we will examine symmetries that relate results in different frames.
For scalar field(s) with action
\begin{equation}\label{eqn:qftLecture6:880}
S = \int d^d x \LL(\phi^i, \partial_\mu \phi^i).
\end{equation}
For example, we’ve been using our massive (Boson) real scalar field with Lagrangian density
\begin{equation}\label{eqn:qftLecture6:900}
\LL = \inv{2} \partial_\mu \phi\partial^\mu \phi – \frac{m^2}{2} \phi^2 – V(\phi).
\end{equation}
Internal symmetry example
\begin{equation}\label{eqn:qftLecture6:920}
H = J \sum_{\expectation{n, n’}} \BS_n \cdot \BS_{n’},
\end{equation}
where the sum means the sum over neighbouring indexes \( n, n’ \) as sketched in
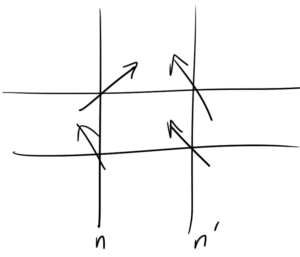
fig. 1. Neighbouring spin cells.
Such a Hamiltonian is left invariant by the transformation \( \BS_n \rightarrow -\BS_n \) since the Hamiltonian is quadratic.
Suppose that \( \phi \rightarrow -\phi\) is a symmetry (it leaves the Lagrangian unchanged). Example
\begin{equation}\label{eqn:qftLecture6:940}
\phi =
\begin{bmatrix}
\phi^1 \\
\phi^2 \\
\vdots
\phi^n \\
\end{bmatrix}
\end{equation}
the Lagrangian
\begin{equation}\label{eqn:qftLecture6:960}
\LL = \inv{2} \partial_\mu \phi^\T \partial^\mu \phi – \frac{m^2}{2} \phi^\T \phi – V(\phi^\T \phi).
\end{equation}
If \( O \) is any \( n \times n \) orthogonal matrix, then it is symmetry since
\begin{equation}\label{eqn:qftLecture6:980}
\phi^\T \phi \rightarrow \phi^\T O^\T O \phi = \phi^\T \phi.
\end{equation}
O(2) model, HW, problem 2. Example for complex \( \phi \)
\begin{equation}\label{eqn:qftLecture6:1000}
\phi \rightarrow e^{i \phi} \phi,
\end{equation}
\begin{equation}\label{eqn:qftLecture6:1020}
\phi = \frac{\psi_1 + i \psi_2}{\sqrt{2}}
\end{equation}
\begin{equation}\label{eqn:qftLecture6:1040}
\begin{bmatrix}
\psi_1 \\
\psi_2
\end{bmatrix}
\rightarrow
\begin{bmatrix}
\cos\alpha & \sin\alpha \\
-\sin\alpha & \cos\alpha
\end{bmatrix}
\begin{bmatrix}
\psi_1 \\
\psi_2
\end{bmatrix}
\end{equation}
September 25, 2018 phy2403 annillation operator, Canonical quantization, creation operator, creation operrator, Hamiltonian density, Hamiltonian equations, Klein Gordon equation, Lagrangian density, lowering operator, raising operator, simple harmonic oscillator, wave functional
[Click here for a PDF of this post with nicer formatting]
These are notes for the UofT course PHY2403H, Quantum Field Theory I, taught by Prof. Erich Poppitz fall 2018.
Last time we introduced a Lagrangian density associated with the Klein-Gordon equation (with a quadratic potential coupling)
\begin{equation}\label{eqn:qftLecture5:20}
L = \int d^3 x
\lr{
\inv{2} \lr{\partial_0 \phi}^2 – \inv{2} \lr{\spacegrad \phi}^2 – \frac{m^2}{2} \phi^2 – \frac{\lambda}{4} \phi^4
}.
\end{equation}
This Lagrangian density was related to the action by
\begin{equation}\label{eqn:qftLecture5:40}
S = \int dt L = \int dt d^3 x \LL,
\end{equation}
with momentum canonically conjugate to the field \( \phi \) defined as
\begin{equation}\label{eqn:qftLecture5:60}
\Pi(\Bx, t) = \frac{\delta \LL}{\delta \phidot(\Bx, t) } = \PD{\phidot(\Bx, t)}{\LL}
\end{equation}
The Hamiltonian defined as
\begin{equation}\label{eqn:qftLecture5:80}
H = \int d^3 x \lr{ \Pi(\Bx, t) \phidot(\Bx, t) – \LL },
\end{equation}
led to
\begin{equation}\label{eqn:qftLecture5:680}
H
= \int d^3 x
\lr{ \inv{2} \Pi^2 + (\spacegrad \phi)^2 + \inv{2} m^2 \phi^2 + \frac{\lambda}{4} \phi^4 }.
\end{equation}
Like the Lagrangian density, we may introduce a Hamiltonian density \( \mathcal{H} \) as
\begin{equation}\label{eqn:qftLecture5:100}
H = \int d^3 x \mathcal{H}(\Bx, t).
\end{equation}
For our Klein-Gordon system, this is
\begin{equation}\label{eqn:qftLecture5:120}
\mathcal{H}(\Bx, t) =
\inv{2} \Pi^2 + (\spacegrad \phi)^2 + \inv{2} m^2 \phi^2 + \frac{\lambda}{4} \phi^4.
\end{equation}
:
We quantize the system by promoting our fields to Heisenberg-Picture (HP) operators, and imposing commutation relations
\begin{equation}\label{eqn:qftLecture5:140}
\antisymmetric{\hat{\Pi}(\Bx, t)}{\hat{\phi}(\By, t)} = -i \delta^3 (\Bx – \By)
\end{equation}
This is in analogy to
\begin{equation}\label{eqn:qftLecture5:160}
\antisymmetric{\hat{p}_i}{\hat{q}_j} = -i \delta_{ij},
\end{equation}
To choose a representation, we may map the \( \Psi \) of QM \( \rightarrow \) to a wave functional \( \Psi[\phi] \)
\begin{equation}\label{eqn:qftLecture5:180}
\hat{\phi}(\By, t) \Psi[\phi] = \phi(\By, t) \Psi[\phi]
\end{equation}
This is similar to the QM wave functions
\begin{equation}\label{eqn:qftLecture5:200}
\begin{aligned}
\hat{q}_i \Psi(\setlr{q}) &= q_i \Psi(q) \\
\hat{p}_i \Psi(\setlr{q}) &= -i \PD{q_i}{} \Psi(p)
\end{aligned}
\end{equation}
Our momentum operator is quantized by expressing it in terms of a variational derivative
\begin{equation}\label{eqn:qftLecture5:220}
\hat{\Pi}(\Bx, t) = -i \frac{\delta}{\delta \phi(\Bx, t)}.
\end{equation}
(Fixme: I’m not really sure exactly what is meant by using the variation derivative \(\delta\) notation here), and to
quantize the Hamiltonian we just add hats, assuming that our fields are all now HP operators
\begin{equation}\label{eqn:qftLecture5:240}
\hat{\mathcal{H}}(\Bx, t)
=
\inv{2} \hat{\Pi}^2 + (\spacegrad \hat{\phi})^2 + \inv{2} m^2 \hat{\phi}^2 + \frac{\lambda}{4} \hat{\phi}^4.
\end{equation}
Recall the QM SHO had a Hamiltonian
\begin{equation}\label{eqn:qftLecture5:260}
\hat{H} = \inv{2} \hat{p}^2 + \inv{2} \omega^2 \hat{q}^2,
\end{equation}
where
\begin{equation}\label{eqn:qftLecture5:280}
\antisymmetric{\hat{p}}{\hat{q}} = -i,
\end{equation}
and that
HP time evolution operators \( O \) satisfied
\begin{equation}\label{eqn:qftLecture5:700}
\ddt{\hatO} = i \antisymmetric{\hatH}{\hatO}.
\end{equation}
In particular
\begin{equation}\label{eqn:qftLecture5:300}
\begin{aligned}
\ddt{\hat{p}}
&= i \antisymmetric{\hat{H}}{\hatp} \\
&= i \frac{\omega^2}{2} \antisymmetric{\hat{q}^2}{\hatp} \\
&= i \frac{\omega^2}{2} (2 i \hat{q}) \\
&= -i \omega^2 \hat{q},
\end{aligned}
\end{equation}
and
\begin{equation}\label{eqn:qftLecture5:320}
\begin{aligned}
\ddt{\hat{q}}
&= i \antisymmetric{\hat{H}}{\hat{q}} \\
&= i \inv{2} \antisymmetric{\hatp^2}{\hat{q}} \\
&= \frac{i}{2}(-2 i \hatp ) \\
&= \hatp.
\end{aligned}
\end{equation}
Applying the time evolution operator twice, we find
\begin{equation}\label{eqn:qftLecture5:340}
\frac{d^2}{dt^2}{\hat{q}}
= \ddt{\hat{p}}
= – \omega^2 \hat{q}.
\end{equation}
We see that the Heisenberg operators obey the classical equations of motion.
Now we want to try this with the quantized QFT fields we’ve promoted to operators
\begin{equation}\label{eqn:qftLecture5:360}
\begin{aligned}
\ddt{\hat{\Pi}}(\Bx, t)
&= i \antisymmetric{\hatH}{\hat{\Pi}(\Bx, t)} \\
&=
i \int d^3 y \inv{2} \antisymmetric{ \lr{\spacegrad \phihat(\By) }^2 }{\hat{\Pi}(\Bx) }
+
i \int d^3 y \frac{m^2}{2} \antisymmetric{ \phihat(\By)^2 }{\hat{\Pi}(\Bx) }
+
i \frac{\lambda}{4} \int d^3 \antisymmetric{ \phihat(\By)^4 }{\hat{\Pi}(\Bx) }
\end{aligned}
\end{equation}
Starting with the non-gradient commutators, and utilizing the HP field analogues of the relations \( \antisymmetric{\hat{q}^n}{\hatp} = n i \hat{q}^{n-1} \), we find
\begin{equation}\label{eqn:qftLecture5:780}
\int d^3 y \antisymmetric{ \lr{ \phihat(\By) }^2 }{\hat{\Pi}(\Bx) }
=
\int d^3 y 2 i \phihat(\By) \delta^3(\Bx – \By)
= 2 i \phihat(\Bx).
\end{equation}
\begin{equation}\label{eqn:qftLecture5:740}
\int d^3 y \antisymmetric{ \lr{ \phihat(\By) }^4 }{\hat{\Pi}(\Bx) }
=
\int d^3 y 4 i \phihat(\By)^3 \delta^3(\Bx – \By)
= 4 i \phihat(\Bx)^3.
\end{equation}
For the gradient commutators, we have more work. Prof Poppitz blitzed through that, just calling it integration by parts. I had trouble seeing what he was doing, so here’s a more explicit dumb expansion required to calculate the commutator
\begin{equation}\label{eqn:qftLecture5:720}
\begin{aligned}
\int d^3 y (\spacegrad \phihat(\By))^2 \hat{\Pi}(\Bx)
&=
\int d^3 y
\lr{ \spacegrad \phihat(\By) \cdot \spacegrad \phihat(\By) } \hat{\Pi}(\Bx) \\
&=
\int d^3 y
\spacegrad \phihat(\By) \cdot
\lr{ \spacegrad (\phihat(\By) \hat{\Pi}(\Bx)) } \\
&=
\int d^3 y
\spacegrad \phihat(\By) \cdot
\lr{ \spacegrad (\hat{\Pi}(\Bx) \phihat(\By) + i \delta^3(\Bx – \By)) } \\
&=
\int d^3 y
\Biglr{
\spacegrad \lr{ \phihat(\By) \hat{\Pi}(\Bx) } \cdot \spacegrad \phihat(\By)
+ i
\spacegrad \phihat(\By) \cdot \spacegrad \delta^3(\Bx – \By)
} \\
&=
\int d^3 y
\Biglr{
\spacegrad \lr{ \hat{\Pi}(\Bx) \phihat(\By) + i \delta^3(\Bx – \By) } \cdot \spacegrad \phihat(\By)
+ i
\spacegrad \phihat(\By) \cdot \spacegrad \delta^3(\Bx – \By)
} \\
&=
\int d^3 y
\hat{\Pi}(\Bx)
\lr{
\spacegrad \phihat(\By) \cdot \spacegrad \phihat(\By)
}
+ 2 i
\int d^3 y
\spacegrad \phihat(\By) \cdot \spacegrad \delta^3(\Bx – \By) \\
&=
\int d^3 y
\hat{\Pi}(\Bx) \spacegrad^2 \phihat(\By)
+
2 i
\int d^3 y
\spacegrad \cdot \lr{ \delta^3(\Bx – \By) \spacegrad \phihat(\By) }
–
2 i
\int d^3 y
\delta^3(\Bx – \By) \spacegrad^2 \phihat(\By) \\
&=
\int d^3 y
\hat{\Pi}(\Bx) \spacegrad^2 \phihat(\By)
+
2 i
\int_\partial d^2 y
\delta^3(\Bx – \By)
\ncap \cdot \spacegrad \phihat(\By)
–
2 i \spacegrad^2 \phihat(\Bx).
\end{aligned}
\end{equation}
Here we take advantage of the fact that the derivative operators \( \spacegrad = \spacegrad_\By \) commute with \( \hat{\Pi}(\Bx) \), and use the identity
\( \spacegrad \cdot (a \spacegrad b) = (\spacegrad a) \cdot (\spacegrad b) + a \spacegrad^2 b \), so the commutator is
\begin{equation}\label{eqn:qftLecture5:800}
\begin{aligned}
\int d^3 y \antisymmetric{(\spacegrad \phihat(\By))^2}{\hat{\Pi}(\Bx)}
&=
2 i
\int_\partial d^2 y
\delta^3(\Bx – \By)
\ncap \cdot \spacegrad \phihat(\By)
–
2 i \spacegrad^2 \phihat(\Bx) \\
&=
–
2 i \spacegrad^2 \phihat(\Bx),
\end{aligned}
\end{equation}
where the boundary integral is presumed to be zero (without enough justification.) All the pieces can now be put back together
\begin{equation}\label{eqn:qftLecture5:820}
\ddt{} \hat{\Pi}(\Bx, t)
=
\spacegrad^2 \phihat(\Bx, t)
–
m^2 \phihat(\Bx, t)
–
\lambda \phihat^3(\Bx, t).
\end{equation}
Now, for the \( \phihat \) time evolution, which is much easier
\begin{equation}\label{eqn:qftLecture5:380}
\begin{aligned}
\ddt{\hat{\phi}}(\Bx, t)
&= i \antisymmetric{\hatH}{\hat{\phi}(\Bx, t)} \\
&= i \inv{2} \int d^3 y \antisymmetric{\hat{\Pi}^2(\By)}{\hat{\phi}(\Bx)} \\
&= i \inv{2} \int d^3 y (-2 i) \hat{\Pi}(\By, t) \delta^3(\Bx – \By) \\
&= \hat{\Pi}(\Bx, t)
\end{aligned}
\end{equation}
\begin{equation}\label{eqn:qftLecture5:400}
\frac{d^2}{dt^2}{\hat{\phi}}(\Bx, t)
=
\spacegrad^2 \phi
-m^2 \phi – \lambda \phihat^3.
\end{equation}
That is
\begin{equation}\label{eqn:qftLecture5:420}
\ddot{\phihat} – \spacegrad^2 \phihat + m^2 \phihat + \lambda \phihat^3 = 0,
\end{equation}
which is the classical Euler-Lagrange equation, also obeyed by the Heisenberg operator \( \phi(\Bx, t) \). When \( \lambda = 0 \) this is the Klein-Gordon equation.
Dropping hats, we now consider the momentum space representation of our operators, as determined by Fourier transform pairs
\begin{equation}\label{eqn:qftLecture5:440}
\begin{aligned}
\phi(\Bx, t) &= \int \frac{d^3 p}{(2\pi)^3} e^{i \Bp \cdot \Bx} \tilde{\phi}(\Bp, t) \\
\tilde{\phi}(\Bp, t) &= \int d^3 x e^{-i \Bp \cdot \Bx} \phi(\Bx, t)
\end{aligned}
\end{equation}
We can discover a representation of the delta function by applying these both in turn
\begin{equation}\label{eqn:qftLecture5:480}
\tilde{\phi}(\Bp, t)
= \int d^3 x e^{-i \Bp \cdot \Bx} \int \frac{d^3 q}{(2 \pi)^3} e^{i \Bq \cdot \Bx} \tilde{\phi}(\Bq, t)
\end{equation}
so
\begin{equation}\label{eqn:qftLecture5:500}
\boxed{
\int d^3 x e^{i \BA \cdot \Bx} = (2 \pi)^3 \delta^3(\BA)
}
\end{equation}
Also observe that \( \phi^\conj(\Bx, t) = \phi(\Bx, t) \) iff \( \tilde{\phi}(\Bp, t) = \tilde{\phi}^\conj(-\Bp, t) \).
We want the EOM for \( \tilde{\phi}(\Bp, t) \) where the operator obeys the KG equation
\begin{equation}\label{eqn:qftLecture5:520}
\lr{ \partial_t^2 – \spacegrad^2 + m^2 } \phi(\Bx, t) = 0
\end{equation}
Inserting the transform relation \ref{eqn:qftLecture5:440} we get
\begin{equation}\label{eqn:qftLecture5:540}
\int \frac{d^3 p}{(2 \pi)^3} e^{i \Bp \cdot \Bx}
\lr{
\ddot{\tilde{\phi}}(\Bp, t) + \lr{ \Bp^2 + m^2 }
\tilde{\phi}(\Bp, t)
}
= 0,
\end{equation}
or
\begin{equation}\label{eqn:qftLecture5:580}
\boxed{
\ddot{\tilde{\phi}}(\Bp, t) = – \omega_\Bp^2 \,\tilde{\phi}(\Bp, t),
}
\end{equation}
where
\begin{equation}\label{eqn:qftLecture5:560}
\omega_\Bp = \sqrt{ \Bp^2 + m^2 }.
\end{equation}
The Fourier components of the HP operators are SHOs!
As we have SHO’s and know how to deal with these in QM, we use the same strategy, introducing raising and lowering operators
\begin{equation}\label{eqn:qftLecture5:600}
\tilde{\phi}(\Bp, t) = \inv{\sqrt{2 \omega_\Bp}} \lr{ e^{-i \omega_\Bp t } a_\Bp + e^{i \omega_\Bp t} a^\dagger_{-\Bp}
}
\end{equation}
Observe that
\begin{equation}\label{eqn:qftLecture5:840}
\begin{aligned}
\tilde{\phi}^\dagger(-\Bp, t)
&= \inv{\sqrt{2 \omega_\Bp}} \lr{ e^{i \omega_\Bp t } a^\dagger_{-\Bp} + e^{-i \omega_\Bp t} a_{\Bp} } \\
&=
\tilde{\phi}(\Bp, t),
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:qftLecture5:620}
\tilde{\phi}^\dagger(\Bp, t) = \tilde{\phi}(-\Bp, t),
\end{equation}
so \( \phi(\Bp, t) \) has a real representation in terms of \( a_\Bp \).
We will find (Wednesday) that
\begin{equation}\label{eqn:qftLecture5:640}
\antisymmetric{a_\Bq}{a^+_\Bp} = \delta^3(\Bp – \Bq) (2 \pi)^3.
\end{equation}
These are equivalent to
\begin{equation}\label{eqn:qftLecture5:660}
\antisymmetric{\hat{\Pi}(\By, t)}{\tilde{\phi}(\Bx, t)} = -i \delta^3(\Bx – \By)
\end{equation}
September 24, 2018 math and physics play area integral, Fundamental Theorem of Geometric Calculus, Geometric Algebra, Geometric Calculus, line integral, volume integral
A new version of Geometric Algebra for Electrical Engineers (V0.1.8) is now posted. This fixes a number of issues in Chapter II on geometric calculus. In particular, I had confused definitions of line, area, and volume integrals that were really the application of the fundamental theorem to such integrals. This is now fixed, and the whole chapter is generally improved and clarified.