volume integral

Circular and spherical area, volume, and boundary integrals.

February 4, 2023 math and physics play , , , , , , ,

[Click here for a PDF version of this post]

Motivation

Maverick posed the following question on the bivector discord

“I saw your blog post on curvilinear coordinates in geometric calculus. I saw your derivation of the volume of a sphere using this technique and decided for practice by doing a surface integral to calculate the area of sphere using the quantity $\partial{\theta} \wedge \partial{\phi}~ dA$ is there a way to integrate this without simply taking the magnitude of this quantity and then integrating or are we limited to only integrating quantities that are 1 dimensional like scalars and pseudoscalars”.

My initial response was that, sure, we should be able to compute bivector and trivector valued integrals. However, in retrospect, the reality is a bit more subtle.

We aren’t limited to using the magnitudes of the differential forms, but not all multivector integral are interesting.
In the original blog post, I must have computed the area of the circle using a bivector valued area element, or the volume of a sphere using a trivector valued volume element. However, if I did the volume that way, I probably cheated and computed 8 times the value of the first octant volume (which is positive), vs. the entire integral, which is zero.  [EDIT: the original post, now linked above, has been corrected.]

Let’s compute the circular area and circumference, and the spherical volume and surface area using multivector valued integrals, and see where we end up having to resort to scalar integrals.

Circular example.

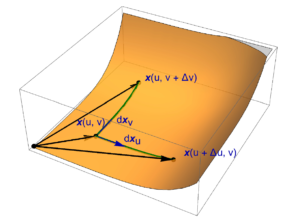
The polar parameterization of points in circular region is
\begin{equation}\label{eqn:circularAndSphericalAreaVolumeAndBoundaries:20}
\Bx = r \Be_1 e^{i\theta},
\end{equation}
where \( i = \Be_1 \Be_2 \).
Our differentials are
\begin{equation}\label{eqn:circularAndSphericalAreaVolumeAndBoundaries:40}
\begin{aligned}
d\Bx_r &= \Be_1 e^{i\theta} \,dr \\
d\Bx_\theta &= r \Be_2 e^{i\theta} \,d\theta.
\end{aligned}
\end{equation}
Our “volume” element, is a 2D pseudoscalar
\begin{equation}\label{eqn:circularAndSphericalAreaVolumeAndBoundaries:60}
\begin{aligned}
dA &= d\Bx_r \wedge d\Bx_\theta \\
&= r \gpgradetwo{ \Be_1 e^{i\theta} \Be_2 e^{i\theta} } \, dr d\theta \\
&= r \gpgradetwo{ \Be_1 \Be_2 e^{-i\theta} e^{i\theta} } \, dr d\theta \\
&= r i \, dr d\theta.
\end{aligned}
\end{equation}
This, as I probably pointed out in my previous blog post, can be integrated to find the area of the circle
\begin{equation}\label{eqn:circularAndSphericalAreaVolumeAndBoundaries:80}
\begin{aligned}
A &= \int_{r = 0}^R \int_{\theta = 0}^{2\pi} r i \, dr d\theta \\
&= \frac{R^2}{2} 2 \pi i \\
&= \pi R^2 i.
\end{aligned}
\end{equation}
However, we got lucky, as the two-form area element was strictly positive (i.e.: the Jacobean for a polar change of coordinates is strictly positive.)

However, we can’t find the circumference of a circle my integrating \( d\Bx_\theta \) around that circular path, because \( d\Bx_\theta \) has an orientation, and we will get zero (given the symmetry of the problem) if we integrate all the way around
\begin{equation}\label{eqn:circularAndSphericalAreaVolumeAndBoundaries:100}
\begin{aligned}
\int_{\theta = 0}^{2\pi} d\Bx_\theta &= \int_{\theta = 0}^{2\pi} r \Be_2 e^{i\theta} \,d\theta \\
&= r \Be_2 \evalrange{ \frac{e^{i\theta}}{i} }{0}{2\pi} \\
&= \frac{r \Be_2}{i} \times 0.
\end{aligned}
\end{equation}
If we want the circumference of a circle, we have to sum all the contributions of \( d\Bx_\theta \) that are colinear with \( \thetacap = \Be_2 e^{i\theta} \)
\begin{equation}\label{eqn:circularAndSphericalAreaVolumeAndBoundaries:120}
\begin{aligned}
C &= \int_{\theta = 0}^{2\pi} \thetacap \cdot \, d\Bx_\theta \\
&= \int_{\theta = 0}^{2\pi} \thetacap \cdot \lr{ r \thetacap \, d\theta } \\
&= 2 \pi r.
\end{aligned}
\end{equation}
This is a plain old boring scalar integral, because the vector valued path integral isn’t terribly interesting.

Spherical example.

For a spherical parameterization, our position vector is
\begin{equation}\label{eqn:circularAndSphericalAreaVolumeAndBoundaries:140}
\Bx = r \Be_1 e^{i \phi} \sin\theta + r \Be_3 \cos\theta,
\end{equation}
so the differentials are
\begin{equation}\label{eqn:circularAndSphericalAreaVolumeAndBoundaries:160}
\begin{aligned}
d\Bx_r &= \lr{ \Be_1 e^{i \phi} \sin\theta + \Be_3 \cos\theta } \,dr = \rcap \, dr \\
d\Bx_\theta &= \lr{ r \Be_1 e^{i \phi} \cos\theta – r \Be_3 \sin\theta }\, d\theta = r \thetacap \,d\theta \\
d\Bx_\phi &= r \Be_2 e^{i \phi} \sin\theta \, d\phi = r \sin\theta \phicap.
\end{aligned}
\end{equation}

The oriented area element on the surface of the sphere is
\begin{equation}\label{eqn:circularAndSphericalAreaVolumeAndBoundaries:180}
\begin{aligned}
dA &= d\Bx_\theta \wedge d\Bx_\phi \\
&= r^2 \gpgradetwo{ \lr{ \Be_1 e^{i \phi} \cos\theta – \Be_3 \sin\theta } \Be_2 e^{i \phi} \sin\theta } \,d\theta d\phi \\
&= r^2 \sin\theta \lr{ i \cos\theta – \Be_{32} e^{i \phi} \sin\theta } \,d\theta d\phi .
\end{aligned}
\end{equation}
Integrating this over the surface will give us zero, with the first integrand killed by the \( \theta \) integral, and the second by the \( \phi \) integral. As pointed out in the original question, we must integrate the absolute value of this two-form in order to find the surface area of the sphere, just as we had to integrate the absolute value of \( d\Bx_\theta \) for the circle to find the circumference.

Let’s perform that integration to verify that we get the expected result. We will first simplify our bivector valued oriented area element. Observe that \( dA \wedge \rcap = dA \rcap \propto I \), so \( dA \propto \rcap I \). We should be able to simplify our expression for \( dA \) by factoring out an \( \rcap \) term
\begin{equation}\label{eqn:circularAndSphericalAreaVolumeAndBoundaries:200}
\begin{aligned}
dA &= r^2 \sin\theta \lr{ \Be_{1233} \cos\theta – \Be_{1132} e^{i \phi} \sin\theta } \,d\theta d\phi \\
&= r^2 \sin\theta I \lr{ \Be_3 \cos\theta + \Be_1 e^{i \phi} \sin\theta } \,d\theta d\phi \\
&= r^2 \sin\theta I \rcap \,d\theta d\phi.
\end{aligned}
\end{equation}
The spherical scalar area is
\begin{equation}\label{eqn:circularAndSphericalAreaVolumeAndBoundaries:220}
\begin{aligned}
A
&= \int_{\theta = 0}^{\pi} \int_{\phi = 0}^{2 \pi} \Abs{ r^2 \sin\theta I \rcap } \,d\theta d\phi \\
&= r^2 \int_{\theta = 0}^{\pi} \int_{\phi = 0}^{2 \pi} \Abs{ \sin\theta } \,d\theta d\phi \\
&= 2 r^2 \int_{\theta = 0}^{\pi/2} \int_{\phi = 0}^{2\pi} \sin\theta \,d\theta d\phi \\
&= 2 r^2 (2 \pi) \\
&= 4 \pi r^2.
\end{aligned}
\end{equation}

Observe that to find the volume of the sphere, we also cannot just integrate the trivector valued volume element directly either. That oriented volume element is
\begin{equation}\label{eqn:circularAndSphericalAreaVolumeAndBoundaries:240}
\begin{aligned}
dV
&= d\Bx_r \wedge dA \\
&= \rcap\, dr dA \\
&= r^2 \sin\theta I \,dr d\theta d\phi.
\end{aligned}
\end{equation}
This integrand is positive above the azimuthal plane, and negative below, so will give us zero if we integrate over the entire \( \theta \in [0, \pi] \) region. So, if we want to find the volume of a sphere, we also must use an absolute integrand.
\begin{equation}\label{eqn:circularAndSphericalAreaVolumeAndBoundaries:260}
\begin{aligned}
V
&= \int_{r = 0}^{R} \int_{\theta = 0}^{\pi} \int_{\phi = 0}^{2 \pi} \Abs{ r^2 \sin\theta I } \,dr d\theta d\phi \\
&= 2 \int_{r = 0}^{R} \int_{\theta = 0}^{\pi/2} \int_{\phi = 0}^{2\pi} r^2 \sin\theta \,dr d\theta d\phi \\
&= 2 \frac{R^3}{3} (2 \pi) \\
&= \frac{4}{3} \pi R^3.
\end{aligned}
\end{equation}
Had the sign of our volume element been invariant over the entire integration region, as it was for the circular area computation (but not the circular boundary computation), we could have computed this as a pseudoscalar integral. For example, if we wanted to know what the oriented volume of the first quadrant of the sphere was, we could compute that directly, as
\begin{equation}\label{eqn:circularAndSphericalAreaVolumeAndBoundaries:280}
\begin{aligned}
V_1 &= \int_{r = 0}^{R} \int_{\theta = 0}^{\pi/2} \int_{\phi = 0}^{\pi/2} r^2 \sin\theta I \,dr d\theta d\phi \\
&= \inv{6} \pi R^3 I,
\end{aligned}
\end{equation}
but if this volume integral is extended to the entire spherical region, the result is zero, not \( (4/3) \pi R^3 I \).

Only when our multivector integrand doesn’t change sign over the integration region, can we directly integrate without taking absolute values.
Again, this should not be too surprising.
This is why, in conventional scalar calculus, we generally must take the absolute value of our change of variable Jacobians, when we compute area or volume computations.

New version of Geometric Algebra for Electrical Engineers posted.

September 24, 2018 math and physics play , , , , ,

 

A new version of Geometric Algebra for Electrical Engineers (V0.1.8) is now posted.  This fixes a number of issues in Chapter II on geometric calculus.  In particular, I had confused definitions of line, area, and volume integrals that were really the application of the fundamental theorem to such integrals.  This is now fixed, and the whole chapter is generally improved and clarified.

Helmholtz theorem

October 1, 2016 math and physics play , , , , , , , , , , , , , ,

[Click here for a PDF of this post with nicer formatting]

This is a problem from ece1228. I attempted solutions in a number of ways. One using Geometric Algebra, one devoid of that algebra, and then this method, which combined aspects of both. Of the three methods I tried to obtain this result, this is the most compact and elegant. It does however, require a fair bit of Geometric Algebra knowledge, including the Fundamental Theorem of Geometric Calculus, as detailed in [1], [3] and [2].

Question: Helmholtz theorem

Prove the first Helmholtz’s theorem, i.e. if vector \(\BM\) is defined by its divergence

\begin{equation}\label{eqn:helmholtzDerviationMultivector:20}
\spacegrad \cdot \BM = s
\end{equation}

and its curl
\begin{equation}\label{eqn:helmholtzDerviationMultivector:40}
\spacegrad \cross \BM = \BC
\end{equation}

within a region and its normal component \( \BM_{\textrm{n}} \) over the boundary, then \( \BM \) is
uniquely specified.

Answer

The gradient of the vector \( \BM \) can be written as a single even grade multivector

\begin{equation}\label{eqn:helmholtzDerviationMultivector:60}
\spacegrad \BM
= \spacegrad \cdot \BM + I \spacegrad \cross \BM
= s + I \BC.
\end{equation}

We will use this to attempt to discover the relation between the vector \( \BM \) and its divergence and curl. We can express \( \BM \) at the point of interest as a convolution with the delta function at all other points in space

\begin{equation}\label{eqn:helmholtzDerviationMultivector:80}
\BM(\Bx) = \int_V dV’ \delta(\Bx – \Bx’) \BM(\Bx’).
\end{equation}

The Laplacian representation of the delta function in \R{3} is

\begin{equation}\label{eqn:helmholtzDerviationMultivector:100}
\delta(\Bx – \Bx’) = -\inv{4\pi} \spacegrad^2 \inv{\Abs{\Bx – \Bx’}},
\end{equation}

so \( \BM \) can be represented as the following convolution

\begin{equation}\label{eqn:helmholtzDerviationMultivector:120}
\BM(\Bx) = -\inv{4\pi} \int_V dV’ \spacegrad^2 \inv{\Abs{\Bx – \Bx’}} \BM(\Bx’).
\end{equation}

Using this relation and proceeding with a few applications of the chain rule, plus the fact that \( \spacegrad 1/\Abs{\Bx – \Bx’} = -\spacegrad’ 1/\Abs{\Bx – \Bx’} \), we find

\begin{equation}\label{eqn:helmholtzDerviationMultivector:720}
\begin{aligned}
-4 \pi \BM(\Bx)
&= \int_V dV’ \spacegrad^2 \inv{\Abs{\Bx – \Bx’}} \BM(\Bx’) \\
&= \gpgradeone{\int_V dV’ \spacegrad^2 \inv{\Abs{\Bx – \Bx’}} \BM(\Bx’)} \\
&= -\gpgradeone{\int_V dV’ \spacegrad \lr{ \spacegrad’ \inv{\Abs{\Bx – \Bx’}}} \BM(\Bx’)} \\
&= -\gpgradeone{\spacegrad \int_V dV’ \lr{
\spacegrad’ \frac{\BM(\Bx’)}{\Abs{\Bx – \Bx’}}
-\frac{\spacegrad’ \BM(\Bx’)}{\Abs{\Bx – \Bx’}}
} } \\
&=
-\gpgradeone{\spacegrad \int_{\partial V} dA’
\ncap \frac{\BM(\Bx’)}{\Abs{\Bx – \Bx’}}
}
+\gpgradeone{\spacegrad \int_V dV’
\frac{s(\Bx’) + I\BC(\Bx’)}{\Abs{\Bx – \Bx’}}
} \\
&=
-\gpgradeone{\spacegrad \int_{\partial V} dA’
\ncap \frac{\BM(\Bx’)}{\Abs{\Bx – \Bx’}}
}
+\spacegrad \int_V dV’
\frac{s(\Bx’)}{\Abs{\Bx – \Bx’}}
+\spacegrad \cdot \int_V dV’
\frac{I\BC(\Bx’)}{\Abs{\Bx – \Bx’}}.
\end{aligned}
\end{equation}

By inserting a no-op grade selection operation in the second step, the trivector terms that would show up in subsequent steps are automatically filtered out. This leaves us with a boundary term dependent on the surface and the normal and tangential components of \( \BM \). Added to that is a pair of volume integrals that provide the unique dependence of \( \BM \) on its divergence and curl. When the surface is taken to infinity, which requires \( \Abs{\BM}/\Abs{\Bx – \Bx’} \rightarrow 0 \), then the dependence of \( \BM \) on its divergence and curl is unique.

In order to express final result in traditional vector algebra form, a couple transformations are required. The first is that

\begin{equation}\label{eqn:helmholtzDerviationMultivector:800}
\gpgradeone{ \Ba I \Bb } = I^2 \Ba \cross \Bb = -\Ba \cross \Bb.
\end{equation}

For the grade selection in the boundary integral, note that

\begin{equation}\label{eqn:helmholtzDerviationMultivector:740}
\begin{aligned}
\gpgradeone{ \spacegrad \ncap \BX }
&=
\gpgradeone{ \spacegrad (\ncap \cdot \BX) }
+
\gpgradeone{ \spacegrad (\ncap \wedge \BX) } \\
&=
\spacegrad (\ncap \cdot \BX)
+
\gpgradeone{ \spacegrad I (\ncap \cross \BX) } \\
&=
\spacegrad (\ncap \cdot \BX)
–
\spacegrad \cross (\ncap \cross \BX).
\end{aligned}
\end{equation}

These give

\begin{equation}\label{eqn:helmholtzDerviationMultivector:721}
\boxed{
\begin{aligned}
\BM(\Bx)
&=
\spacegrad \inv{4\pi} \int_{\partial V} dA’ \ncap \cdot \frac{\BM(\Bx’)}{\Abs{\Bx – \Bx’}}
–
\spacegrad \cross \inv{4\pi} \int_{\partial V} dA’ \ncap \cross \frac{\BM(\Bx’)}{\Abs{\Bx – \Bx’}} \\
&-\spacegrad \inv{4\pi} \int_V dV’
\frac{s(\Bx’)}{\Abs{\Bx – \Bx’}}
+\spacegrad \cross \inv{4\pi} \int_V dV’
\frac{\BC(\Bx’)}{\Abs{\Bx – \Bx’}}.
\end{aligned}
}
\end{equation}

References

[1] C. Doran and A.N. Lasenby. Geometric algebra for physicists. Cambridge University Press New York, Cambridge, UK, 1st edition, 2003.

[2] A. Macdonald. Vector and Geometric Calculus. CreateSpace Independent Publishing Platform, 2012.

[3] Garret Sobczyk and Omar Le’on S’anchez. Fundamental theorem of calculus. Advances in Applied Clifford Algebras, 21:221–231, 2011. URL https://arxiv.org/abs/0809.4526.

Maxwell equation boundary conditions

September 6, 2016 math and physics play , , , , , , , , , , , , , ,

[Click here for a PDF of this post with nicer formatting]

Motivation

boundaryConditionsTwoSurfacesFig1

fig 1. Two surfaces normal to the interface.

Most electrodynamics textbooks either start with or contain a treatment of boundary value conditions. These typically involve evaluating Maxwell’s equations over areas or volumes of decreasing height, such as those illustrated in fig. 1, and fig. 2. These represent surfaces and volumes where the height is allowed to decrease to infinitesimal levels, and are traditionally used to find the boundary value constraints of the normal and tangential components of the electric and magnetic fields.

boundaryConditionsPillBoxFig2

fig 2. A pillbox volume encompassing the interface.

More advanced topics, such as evaluation of the Fresnel reflection and transmission equations, also rely on similar consideration of boundary value constraints. I’ve wondered for a long time how the Fresnel equations could be attacked by looking at the boundary conditions for the combined field \( F = \BE + I c \BB \), instead of the considering them separately.

A unified approach.

The Geometric Algebra (and relativistic tensor) formulations of Maxwell’s equations put the electric and magnetic fields on equal footings. It is in fact possible to specify the boundary value constraints on the fields without first separating Maxwell’s equations into their traditional forms. The starting point in Geometric Algebra is Maxwell’s equation, premultiplied by a stationary observer’s timelike basis vector

\begin{equation}\label{eqn:maxwellBoundaryConditions:20}
\gamma_0 \grad F = \inv{\epsilon_0 c} \gamma_0 J,
\end{equation}

or

\begin{equation}\label{eqn:maxwellBoundaryConditions:40}
\lr{ \partial_0 + \spacegrad} F = \frac{\rho}{\epsilon_0} – \frac{\BJ}{\epsilon_0}.
\end{equation}

The electrodynamic field \(F = \BE + I c \BB\) is a multivector in this spatial domain (whereas it is a bivector in the spacetime algebra domain), and has vector and bivector components. The product of the spatial gradient and the field can still be split into dot and curl components \(\spacegrad M = \spacegrad \cdot M + \spacegrad \wedge M \). If \(M = \sum M_i \), where \(M_i\) is an grade \(i\) blade, then we give this the Hestenes’ [1] definitions

\begin{equation}\label{eqn:maxwellBoundaryConditions:60}
\begin{aligned}
\spacegrad \cdot M &= \sum_i \gpgrade{\spacegrad M_i}{i-1} \\
\spacegrad \wedge M &= \sum_i \gpgrade{\spacegrad M_i}{i+1}.
\end{aligned}
\end{equation}

With that said, Maxwell’s equation can be rearranged into a pair of multivector equations

\begin{equation}\label{eqn:maxwellBoundaryConditions:80}
\begin{aligned}
\spacegrad \cdot F &= \gpgrade{-\partial_0 F + \frac{\rho}{\epsilon_0} – \frac{\BJ}{\epsilon_0 c}}{0,1} \\
\spacegrad \wedge F &= \gpgrade{-\partial_0 F + \frac{\rho}{\epsilon_0} – \frac{\BJ}{\epsilon_0 c}}{2,3},
\end{aligned}
\end{equation}

The latter equation can be integrated with Stokes theorem, but we need to apply a duality transformation to the latter in order to apply Stokes to it

\begin{equation}\label{eqn:maxwellBoundaryConditions:120}
\begin{aligned}
\spacegrad \cdot F
&=
-I^2 \spacegrad \cdot F \\
&=
-I^2 \gpgrade{\spacegrad F}{0,1} \\
&=
-I \gpgrade{I \spacegrad F}{2,3} \\
&=
-I \spacegrad \wedge (IF),
\end{aligned}
\end{equation}

so

\begin{equation}\label{eqn:maxwellBoundaryConditions:100}
\begin{aligned}
\spacegrad \wedge (I F) &= I \lr{ -\inv{c} \partial_t \BE + \frac{\rho}{\epsilon_0} – \frac{\BJ}{\epsilon_0 c} } \\
\spacegrad \wedge F &= -I \partial_t \BB.
\end{aligned}
\end{equation}

Integrating each of these over the pillbox volume gives

\begin{equation}\label{eqn:maxwellBoundaryConditions:140}
\begin{aligned}
\oint_{\partial V} d^2 \Bx \cdot (I F)
&=
\int_{V} d^3 \Bx \cdot \lr{ I \lr{ -\inv{c} \partial_t \BE + \frac{\rho}{\epsilon_0} – \frac{\BJ}{\epsilon_0 c} } } \\
\oint_{\partial V} d^2 \Bx \cdot F
&=
– \partial_t \int_{V} d^3 \Bx \cdot \lr{ I \BB }.
\end{aligned}
\end{equation}

In the absence of charges and currents on the surface, and if the height of the volume is reduced to zero, the volume integrals vanish, and only the upper surfaces of the pillbox contribute to the surface integrals.

\begin{equation}\label{eqn:maxwellBoundaryConditions:200}
\begin{aligned}
\oint_{\partial V} d^2 \Bx \cdot (I F) &= 0 \\
\oint_{\partial V} d^2 \Bx \cdot F &= 0.
\end{aligned}
\end{equation}

With a multivector \(F\) in the mix, the geometric meaning of these integrals is not terribly clear. They do describe the boundary conditions, but to see exactly what those are, we can now resort to the split of \(F\) into its electric and magnetic fields. Let’s look at the non-dual integral to start with

\begin{equation}\label{eqn:maxwellBoundaryConditions:160}
\begin{aligned}
\oint_{\partial V} d^2 \Bx \cdot F
&=
\oint_{\partial V} d^2 \Bx \cdot \lr{ \BE + I c \BB } \\
&=
\oint_{\partial V} d^2 \Bx \cdot \BE + I c d^2 \Bx \wedge \BB \\
&=
0.
\end{aligned}
\end{equation}

No component of \(\BE\) that is normal to the surface contributes to \(d^2 \Bx \cdot \BE \), whereas only components of \(\BB\) that are normal contribute to \(d^2 \Bx \wedge \BB \). That means that we must have tangential components of \(\BE\) and the normal components of \(\BB\) matching on the surfaces

\begin{equation}\label{eqn:maxwellBoundaryConditions:180}
\begin{aligned}
\lr{\BE_2 \wedge \ncap} \ncap – \lr{\BE_1 \wedge (-\ncap)} (-\ncap) &= 0 \\
\lr{\BB_2 \cdot \ncap} \ncap – \lr{\BB_1 \cdot (-\ncap)} (-\ncap) &= 0 .
\end{aligned}
\end{equation}

Similarly, for the dot product of the dual field, this is

\begin{equation}\label{eqn:maxwellBoundaryConditions:220}
\begin{aligned}
\oint_{\partial V} d^2 \Bx \cdot (I F)
&=
\oint_{\partial V} d^2 \Bx \cdot (I \BE – c \BB) \\
&=
\oint_{\partial V} I d^2 \Bx \wedge \BE – c d^2 \Bx \cdot \BB.
\end{aligned}
\end{equation}

For this integral, only the normal components of \(\BE\) contribute, and only the tangential components of \(\BB\) contribute. This means that

\begin{equation}\label{eqn:maxwellBoundaryConditions:240}
\begin{aligned}
\lr{\BE_2 \cdot \ncap} \ncap – \lr{\BE_1 \cdot (-\ncap)} (-\ncap) &= 0 \\
\lr{\BB_2 \wedge \ncap} \ncap – \lr{\BB_1 \wedge (-\ncap)} (-\ncap) &= 0.
\end{aligned}
\end{equation}

This is why we end up with a seemingly strange mix of tangential and normal components of the electric and magnetic fields. These constraints can be summarized as

\begin{equation}\label{eqn:maxwellBoundaryConditions:260}
\begin{aligned}
( \BE_2 – \BE_1 ) \cdot \ncap &= 0 \\
( \BE_2 – \BE_1 ) \wedge \ncap &= 0 \\
( \BB_2 – \BB_1 ) \cdot \ncap &= 0 \\
( \BB_2 – \BB_1 ) \wedge \ncap &= 0
\end{aligned}
\end{equation}

These relationships are usually expressed in terms of all of \(\BE, \BD, \BB\) and \(\BH \). Because I’d started with Maxwell’s equations for free space, I don’t have the \( \epsilon \) and \( \mu \) factors that produce those more general relationships. Those more general boundary value relationships are usually the starting point for the Fresnel interface analysis. It is also possible to further generalize these relationships to include charges and currents on the surface.

References

[1] D. Hestenes. New Foundations for Classical Mechanics. Kluwer Academic Publishers, 1999.