[Click here for a PDF of this post with nicer formatting]
DISCLAIMER: Very rough notes from class. Some additional side notes, but otherwise barely edited.
Natural units.
\begin{equation}\label{eqn:qftLecture2:20}
\begin{aligned}
[\Hbar] &= [\text{action}] = M \frac{L^2}{T^2} T = \frac{M L^2}{T} \\
&= [\text{velocity}] = \frac{L}{T} \\
& [\text{energy}] = M \frac{L^2}{T^2}.
\end{aligned}
\end{equation}
Setting \( c = 1 \) means
\begin{equation}\label{eqn:qftLecture2:240}
\frac{L}{T} = 1
\end{equation}
and setting \( \Hbar = 1 \) means
\begin{equation}\label{eqn:qftLecture2:260}
[\Hbar] = [\text{action}] = M L {\frac{L}{T}} = M L
\end{equation}
therefore
\begin{equation}\label{eqn:qftLecture2:280}
[L] = \inv{\text{mass}}
\end{equation}
and
\begin{equation}\label{eqn:qftLecture2:300}
[\text{energy}] = M {\frac{L^2}{T^2}} = \text{mass}\, \text{eV}
\end{equation}
Summary
- \( \text{energy} \sim \text{eV} \)
- \( \text{distance} \sim \inv{M} \)
- \( \text{time} \sim \inv{M} \)
From:
\begin{equation}\label{eqn:qftLecture2:320}
\alpha = \frac{e^2}{4 \pi {\Hbar c}}
\end{equation}
which is dimensionless (\(1/137\)), so electric charge is dimensionless.
Some useful numbers in natural units
\begin{equation}\label{eqn:qftLecture2:40}
\begin{aligned}
m_\txte &\sim 10^{-27} \text{g} \sim 0.5 \text{MeV} \\
m_\txtp &\sim 2000 m_\txte \sim 1 \text{GeV} \\
m_\pi &\sim 140 \text{MeV} \\
m_\mu &\sim 105 \text{MeV} \\
\Hbar c &\sim 200 \text{MeV} \,\text{fm} = 1
\end{aligned}
\end{equation}
Gravity
Interaction energy of two particles
\begin{equation}\label{eqn:qftLecture2:60}
G_\txtN \frac{m_1 m_2}{r}
\end{equation}
\begin{equation}\label{eqn:qftLecture2:80}
[\text{energy}] \sim [G_\txtN] \frac{M^2}{L}
\end{equation}
\begin{equation}\label{eqn:qftLecture2:100}
[G_\txtN]
\sim
[\text{energy}] \frac{L}{M^2}
\end{equation}
but energy x distance is dimensionless (action) in our units
\begin{equation}\label{eqn:qftLecture2:120}
[G_\txtN]
\sim
{\text{dimensionless}}{M^2}
\end{equation}
\begin{equation}\label{eqn:qftLecture2:140}
\frac{G_\txtN}{\Hbar c} \sim \inv{M^2} \sim \frac{1}{10^{20} \text{GeV}}
\end{equation}
Planck mass
\begin{equation}\label{eqn:qftLecture2:160}
M_{\text{Planck}} \sim \sqrt{\frac{\Hbar c}{G_\txtN}}
\sim 10^{-4} g \sim \inv{\lr{10^{20} \text{GeV}}^2}
\end{equation}
We can revisit the scale diagram from last lecture in terms of MeV mass/energy values, as sketched in fig. 1.
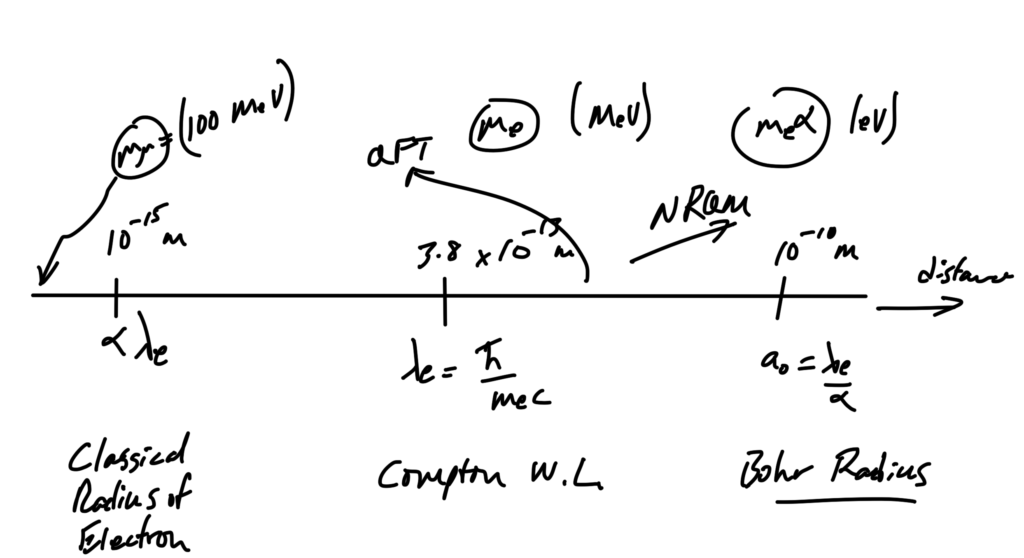
fig. 1. Scales, take II.
At the classical electron radius scale, we consider phenomena such as back reaction of radiation, the self energy of electrons. At the Compton wavelength we have to allow for production of multiple particle pairs. At Bohr radius scales we must start using QM instead of classical mechanics.
Cross section.
Verbal discussion of cross section, not captured in these notes. Roughly, the cross section sounds like the number of events per unit time, related to the flux of some source through an area.
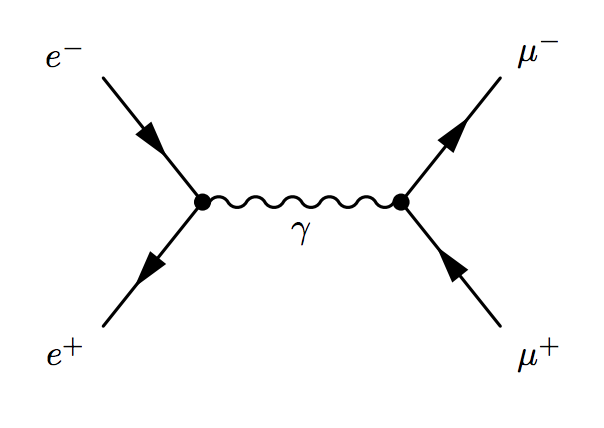
We’ll compute the cross section of a number of different systems in this course. The cross section is relevant in scattering such as the electron-electron scattering sketched in fig. 2.
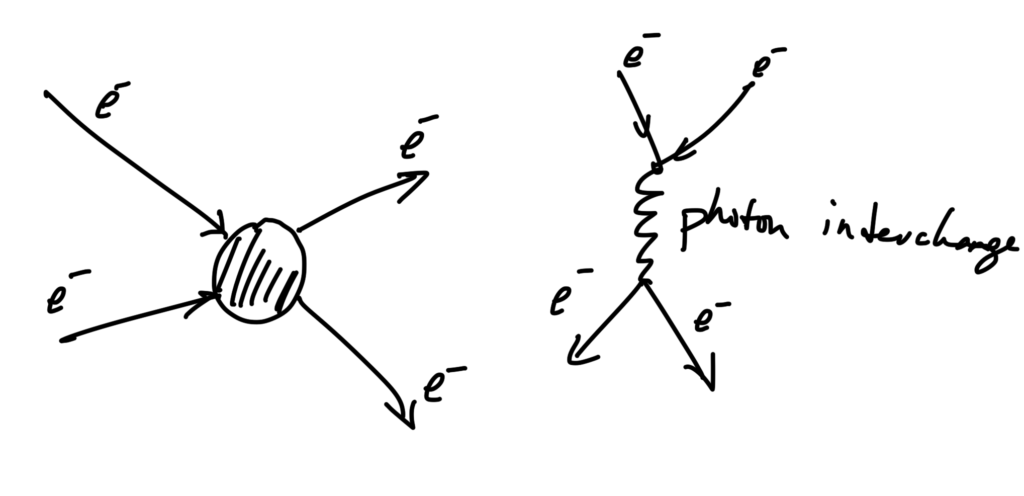
fig. 2. Electron electron scattering.
We assume that QED is highly relativistic. In natural units, our scale factor is basically the square of the electric charge
\begin{equation}\label{eqn:qftLecture2:180}
\alpha \sim e^2,
\end{equation}
so the cross section has the form
\begin{equation}\label{eqn:qftLecture2:200}
\sigma \sim \frac{\alpha^2}{E^2} \lr{ 1 + O(\alpha) + O(\alpha^2) + \cdots }
\end{equation}
In gravity we could consider scattering of electrons, where \( G_\txtN \) takes the place of \( \alpha \). However, \( G_\txtN \) has dimensions.
For electron-electron scattering due to gravitons
\begin{equation}\label{eqn:qftLecture2:220}
\sigma \sim \frac{G_\txtN^2 E^2}{1 + G_\txtN E^2 + \cdots }
\end{equation}
Now the cross section grows with energy. This will cause some problems (violating unitarity: probabilities greater than 1!) when \( O(G_\txtN E^2) = 1 \).
In any quantum field theories when the coupling constant is not-dimensionless we have the same sort of problems at some scale.
The point is that we can get far considering just dimensional analysis.
If the coupling constant has a dimension \((1/\text{mass})^N\,, N > 0\), then unitarity will be violated at high energy. One such theory is the Fermi theory of beta decay (electro-weak theory), which had a coupling constant with dimensions inverse-mass-squared. The relevant scale for beta decay was 4 Fermi, or \( G_\txtF \sim (1/{100 \text{GeV}})^2 \). This was the motivation for introducing the Higgs theory, which was motivated by restoring unitarity.
Lorentz transformations.
The goal, perhaps not for today, is to study the simplest (relativistic) scalar field theory. First studied classically, and then consider such a quantum field theory.
How is relativity implemented when we write the Lagrangian and action?
Our first step must be to consider Lorentz transformations and the Lorentz group.
Spacetime (Minkowski space) is \R{3,1} (or \R{d-1,1}). Our coordinates are
\begin{equation}\label{eqn:qftLecture2:340}
(c t, x^1, x^2, x^3) = (c t, \Br).
\end{equation}
Here, we’ve scaled the time scale by \( c \) so that we measure time and space in the same dimensions. We write this as
\begin{equation}\label{eqn:qftLecture2:360}
x^\mu = (x^0, x^1, x^2, x^3),
\end{equation}
where \( \mu = 0, 1, 2, 3 \), and call this a “4-vector”. These are called the space-time coordinates of an event, which tell us where and when an event occurs.
For two events whose spacetime coordinates differ by \( dx^0, dx^1, dx^2, dx^3 \) we introduce the notion of a space time \underline{interval}
\begin{equation}\label{eqn:qftLecture2:380}
\begin{aligned}
ds^2
&= c^2 dt^2
– (dx^1)^2
– (dx^2)^2
– (dx^3)^2 \\
&=
\sum_{\mu, \nu = 0}^3 g_{\mu\nu} dx^\mu dx^\nu
\end{aligned}
\end{equation}
Here \( g_{\mu\nu} \) is the Minkowski space metric, an object with two indexes that run from 0-3. i.e. this is a diagonal matrix
\begin{equation}\label{eqn:qftLecture2:400}
g_{\mu\nu} \sim
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & -1 & 0 & 0 \\
0 & 0 & -1 & 0 \\
0 & 0 & 0 & -1 \\
\end{bmatrix}
\end{equation}
i.e.
\begin{equation}\label{eqn:qftLecture2:420}
\begin{aligned}
g_{00} &= 1 \\
g_{11} &= -1 \\
g_{22} &= -1 \\
g_{33} &= -1 \\
\end{aligned}
\end{equation}
We will use the Einstein summation convention, where any repeated upper and lower indexes are considered summed over. That is \ref{eqn:qftLecture2:380} is written with an implied sum
\begin{equation}\label{eqn:qftLecture2:440}
ds^2 = g_{\mu\nu} dx^\mu dx^\nu.
\end{equation}
Explicit expansion:
\begin{equation}\label{eqn:qftLecture2:460}
\begin{aligned}
ds^2
&= g_{\mu\nu} dx^\mu dx^\nu \\
&=
g_{00} dx^0 dx^0
+g_{11} dx^1 dx^1
+g_{22} dx^2 dx^2
+g_{33} dx^3 dx^3
&=
(1) dx^0 dx^0
+ (-1) dx^1 dx^1
+ (-1) dx^2 dx^2
+ (-1) dx^3 dx^3.
\end{aligned}
\end{equation}
Recall that rotations (with orthogonal matrix representations) are transformations that leave the dot product unchanged, that is
\begin{equation}\label{eqn:qftLecture2:480}
\begin{aligned}
(R \Bx) \cdot (R \By)
&= \Bx^\T R^\T R \By \\
&= \Bx^\T \By \\
&= \Bx \cdot \By,
\end{aligned}
\end{equation}
where \( R \) is a rotation orthogonal 3×3 matrix. The set of such transformations that leave the dot product unchanged have orthonormal matrix representations \( R^\T R = 1 \). We call the set of such transformations that have unit determinant the SO(3) group.
We call a Lorentz transformation, if it is a linear transformation acting on 4 vectors that leaves the spacetime interval (i.e. the inner product of 4 vectors) invariant. That is, a transformation that leaves
\begin{equation}\label{eqn:qftLecture2:500}
x^\mu y^\nu g_{\mu\nu} = x^0 y^0 – x^1 y^1 – x^2 y^2 – x^3 y^3
\end{equation}
unchanged.
Suppose that transformation has a 4×4 matrix form
\begin{equation}\label{eqn:qftLecture2:520}
{x’}^\mu = {\Lambda^\mu}_\nu x^\nu
\end{equation}
For an example of a possible \( \Lambda \), consider the transformation sketched in fig. 3.
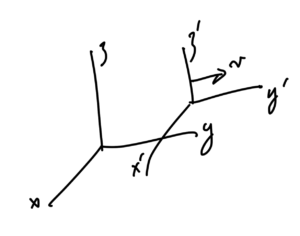
fig. 3. Boost transformation.
We know that boost has the form
\begin{equation}\label{eqn:qftLecture2:540}
\begin{aligned}
x &= \frac{x’ + v t’}{\sqrt{1 – v^2/c^2}} \\
y &= y’ \\
z &= z’ \\
t &= \frac{t’ + (v/c^2) x’}{\sqrt{1 – v^2/c^2}} \\
\end{aligned}
\end{equation}
(this is a boost along the x-axis, not y as I’d drawn),
or
\begin{equation}\label{eqn:qftLecture2:560}
\begin{bmatrix}
c t \\
x \\
y \\
z
\end{bmatrix}
=
\begin{bmatrix}
\inv{\sqrt{1 – v^2/c^2}} & \frac{v/c}{\sqrt{1 – v^2/c^2}} & 0 & 0 \\
\frac{v/c}{\sqrt{1 – v^2/c^2}} & \frac{1}{\sqrt{1 – v^2/c^2}} & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
c t’ \\
x’ \\
y’ \\
z’
\end{bmatrix}
\end{equation}
Other examples include rotations (\({\lambda^0}_0 = 1\) zeros in \( {\lambda^0}_k, {\lambda^k}_0 \), and a rotation matrix in the remainder.)
Back to Lorentz transformations (\(\text{SO}(1,3)^+\)), let
\begin{equation}\label{eqn:qftLecture2:600}
\begin{aligned}
{x’}^\mu &= {\Lambda^\mu}_\nu x^\nu \\
{y’}^\kappa &= {\Lambda^\kappa}_\rho y^\rho
\end{aligned}
\end{equation}
The dot product
\begin{equation}\label{eqn:qftLecture2:620}
g_{\mu \kappa}
{x’}^\mu
{y’}^\kappa
=
g_{\mu \kappa}
{\Lambda^\mu}_\nu
{\Lambda^\kappa}_\rho
x^\nu
y^\rho
=
g_{\nu\rho}
x^\nu
y^\rho,
\end{equation}
where the last step introduces the invariance requirement of the transformation. That is
\begin{equation}\label{eqn:qftLecture2:640}
\boxed{
g_{\nu\rho}
=
g_{\mu \kappa}
{\Lambda^\mu}_\nu
{\Lambda^\kappa}_\rho.
}
\end{equation}
Upper and lower indexes
We’ve defined
\begin{equation}\label{eqn:qftLecture2:660}
x^\mu = (t, x^1, x^2, x^3)
\end{equation}
We could also define a four vector with lower indexes
\begin{equation}\label{eqn:qftLecture2:680}
x_\nu = g_{\nu\mu} x^\mu = (t, -x^1, -x^2, -x^3).
\end{equation}
That is
\begin{equation}\label{eqn:qftLecture2:700}
\begin{aligned}
x_0 &= x^0 \\
x_1 &= -x^1 \\
x_2 &= -x^2 \\
x_3 &= -x^3.
\end{aligned}
\end{equation}
which allows us to write the dot product as simply \( x^\mu y_\mu \).
We can also define a metric tensor with upper indexes
\begin{equation}\label{eqn:qftLecture2:401}
g^{\mu\nu} \sim
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & -1 & 0 & 0 \\
0 & 0 & -1 & 0 \\
0 & 0 & 0 & -1 \\
\end{bmatrix}
\end{equation}
This is the inverse matrix of \( g_{\mu\nu} \), and it satisfies
\begin{equation}\label{eqn:qftLecture2:720}
g^{\mu \nu} g_{\nu\rho} = {\delta^\mu}_\rho
\end{equation}
Exercise: Check:
\begin{equation}\label{eqn:qftLecture2:740}
\begin{aligned}
g_{\mu\nu} x^\mu y^\nu
&= x_\nu y^\nu \\
&= x^\nu y_\nu \\
&= g^{\mu\nu} x_\mu y_\nu \\
&= {\delta^\mu}_\nu x_\mu y^\nu.
\end{aligned}
\end{equation}
Class ended around this point, but it appeared that we were heading this direction:
Returning to the Lorentz invariant and multiplying both sides of
\ref{eqn:qftLecture2:640} with an inverse Lorentz transformation \( \Lambda^{-1} \), we find
\begin{equation}\label{eqn:qftLecture2:760}
\begin{aligned}
g_{\nu\rho}
{\lr{\Lambda^{-1}}^\rho}_\alpha
&=
g_{\mu \kappa}
{\Lambda^\mu}_\nu
{\Lambda^\kappa}_\rho
{\lr{\Lambda^{-1}}^\rho}_\alpha \\
&=
g_{\mu \kappa}
{\Lambda^\mu}_\nu
{\delta^\kappa}_\alpha \\
&=
g_{\mu \alpha}
{\Lambda^\mu}_\nu,
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:qftLecture2:780}
\lr{\Lambda^{-1}}_{\nu \alpha} = \Lambda_{\alpha \nu}.
\end{equation}
This is clearly analogous to \( R^\T = R^{-1} \), although the index notation obscures things considerably. Prof. Poppitz said that next week this would all lead to showing that the determinant of any Lorentz transformation was \( \pm 1 \).
For what it’s worth, it seems to me that this index notation makes life a lot harder than it needs to be, at least for a matrix related question (i.e. determinant of the transformation). In matrix/column-(4)-vector notation, let \(x’ = \Lambda x, y’ = \Lambda y\) be two four vector transformations, then
\begin{equation}\label{eqn:qftLecture2:800}
x’ \cdot y’ = {x’}^T G y’ = (\Lambda x)^T G \Lambda y = x^T ( \Lambda^T G \Lambda) y = x^T G y.
\end{equation}
so
\begin{equation}\label{eqn:qftLecture2:820}
\boxed{
\Lambda^T G \Lambda = G.
}
\end{equation}
Taking determinants of both sides gives \(-(det(\Lambda))^2 = -1\), and thus \(det(\Lambda) = \pm 1\).
Like this:
Like Loading...