[Click here for a PDF of this post with nicer formatting]
DISCLAIMER: Very rough notes from class. May have some additional side notes, but otherwise probably barely edited.
These are notes for the UofT course PHY2403H, Quantum Field Theory I, taught by Prof. Erich Poppitz fall 2018.
Principles (cont.)
- Lorentz (Poincar\’e : Lorentz and spacetime translations)
- locality
- dimensional analysis
- gauge invariance
These are the requirements for an action. We postulated an action that had the form
\begin{equation}\label{eqn:qftLecture4:20}
\int d^d x \partial_\mu \phi \partial^\mu \phi,
\end{equation}
called the “Kinetic term”, which mimics \( \int dt \dot{q}^2 \) that we’d see in quantum or classical mechanics. In principle there exists an infinite number of local Poincar\’e invariant terms that we can write. Examples:
- \( \partial_\mu \phi \partial^\mu \phi \)
- \( \partial_\mu \phi \partial_\nu \partial^\nu \partial^\mu \phi \)
- \( \lr{\partial_\mu \phi \partial^\mu \phi}^2 \)
- \( f(\phi) \partial_\mu \phi \partial^\mu \phi \)
- \( f(\phi, \partial_\mu \phi \partial^\mu \phi) \)
- \( V(\phi) \)
It turns out that nature (i.e. three spatial dimensions and one time dimension) is described by a finite number of terms. We will now utilize dimensional analysis to determine some of the allowed forms of the action for scalar field theories in \( d = 2, 3, 4, 5 \) dimensions. Even though the real world is only \( d = 4 \), some of the \( d < 4 \) theories are relevant in condensed matter studies, and \( d = 5 \) is just for fun (but also applies to string theories.)
With \( [x] \sim \inv{M} \) in natural units, we must define \([\phi]\) such that the kinetic term is dimensionless in d spacetime dimensions
\begin{equation}\label{eqn:qftLecture4:40}
\begin{aligned}
[d^d x] &\sim \inv{M^d} \\
[\partial_\mu] &\sim M
\end{aligned}
\end{equation}
so it must be that
\begin{equation}\label{eqn:qftLecture4:60}
[\phi] = M^{(d-2)/2}
\end{equation}
It will be easier to characterize the dimensionality of any given term by the power of the mass units, that is
\begin{equation}\label{eqn:qftLecture4:80}
\begin{aligned}
[\text{mass}] &= 1 \\
[d^d x] &= -d \\
[\partial_\mu] &= 1 \\
[\phi] &= (d-2)/2 \\
[S] &= 0.
\end{aligned}
\end{equation}
Since the action is
\begin{equation}\label{eqn:qftLecture4:100}
S = \int d^d x \lr{ \LL(\phi, \partial_\mu \phi) },
\end{equation}
and because action had dimensions of \( \Hbar \), so in natural units, it must be dimensionless, the Lagrangian density dimensions must be \( [d] \). We will abuse language in QFT and call the Lagrangian density the Lagrangian.
\( d = 2 \)
Because \( [\partial_\mu \phi \partial^\mu \phi ] = 2 \), the scalar field must be dimension zero, or in symbols
\begin{equation}\label{eqn:qftLecture4:120}
[\phi] = 0.
\end{equation}
This means that introducing any function \( f(\phi) = 1 + a \phi + b\phi^2 + c \phi^3 + \cdots \) is also dimensionless, and
\begin{equation}\label{eqn:qftLecture4:140}
[f(\phi) \partial_\mu \phi \partial^\mu \phi ] = 2,
\end{equation}
for any \( f(\phi) \). Another implication of this is that the a potential term in the Lagrangian \( [V(\phi)] = 0 \) needs a coupling constant of dimension 2. Letting \( \mu \) have mass dimensions, our Lagrangian must have the form
\begin{equation}\label{eqn:qftLecture4:160}
f(\phi) \partial_\mu \phi \partial^\mu \phi + \mu^2 V(\phi).
\end{equation}
An infinite number of coupling constants of positive mass dimensions for \( V(\phi) \) are also allowed. If we have higher order derivative terms, then we need to compensate for the negative mass dimensions. Example (still for \( d = 2 \)).
\begin{equation}\label{eqn:qftLecture4:180}
\LL =
f(\phi) \partial_\mu \phi \partial^\mu \phi + \mu^2 V(\phi) + \inv{{\mu’}^2}\partial_\mu \phi \partial_\nu \partial^\nu \partial^\mu \phi + \lr{ \partial_\mu \phi \partial^\mu \phi }^2 \inv{\tilde{\mu}^2}.
\end{equation}
The last two terms, called \underline{couplings} (i.e. any non-kinetic term), are examples of terms with negative mass dimension. There is an infinite number of those in any theory in any dimension.
Definitions
- Couplings that are dimensionless are called (classically) marginal.
- Couplings that have positive mass dimension are called (classically) relevant.
- Couplings that have negative mass dimension are called (classically) irrelevant.
In QFT we are generally interested in the couplings that are measurable at long distances for some given energy. Classically irrelevant theories are generally not interesting in \( d > 2 \), so we are very lucky that we don’t live in three dimensional space. This means that we can get away with a finite number of classically marginal and relevant couplings in 3 or 4 dimensions. This was mentioned in the Wilczek’s article referenced in the class forum [1]\footnote{There’s currently more in that article that I don’t understand than I do, so it is hard to find it terribly illuminating.}
Long distance physics in any dimension is described by the marginal and relevant couplings. The irrelevant couplings die off at low energy. In two dimensions, a priori, an infinite number of marginal and relevant couplings are possible. 2D is a bad place to live!
\( d = 3 \)
Now we have
\begin{equation}\label{eqn:qftLecture4:200}
[\phi] = \inv{2}
\end{equation}
so that
\begin{equation}\label{eqn:qftLecture4:220}
[\partial_\mu \phi \partial^\mu \phi] = 3.
\end{equation}
A 3D Lagrangian could have local terms such as
\begin{equation}\label{eqn:qftLecture4:240}
\LL = \partial_\mu \phi \partial^\mu \phi + m^2 \phi^2 + \mu^{3/2} \phi^3 + \mu’ \phi^4
+ \lr{\mu”}{1/2} \phi^5
+ \lambda \phi^6.
\end{equation}
where \( m, \mu, \mu” \) all have mass dimensions, and \( \lambda \) is dimensionless. i.e. \( m, \mu, \mu” \) are relevant, and \( \lambda \) marginal. We stop at the sixth power, since any power after that will be irrelevant.
\( d = 4 \)
Now we have
\begin{equation}\label{eqn:qftLecture4:260}
[\phi] = 1
\end{equation}
so that
\begin{equation}\label{eqn:qftLecture4:280}
[\partial_\mu \phi \partial^\mu \phi] = 4.
\end{equation}
In this number of dimensions \( \phi^k \partial_\mu \phi \partial^\mu \) is an irrelevant coupling.
A 4D Lagrangian could have local terms such as
\begin{equation}\label{eqn:qftLecture4:300}
\LL = \partial_\mu \phi \partial^\mu \phi + m^2 \phi^2 + \mu \phi^3 + \lambda \phi^4.
\end{equation}
where \( m, \mu \) have mass dimensions, and \( \lambda \) is dimensionless. i.e. \( m, \mu \) are relevant, and \( \lambda \) is marginal.
\( d = 5 \)
Now we have
\begin{equation}\label{eqn:qftLecture4:320}
[\phi] = \frac{3}{2},
\end{equation}
so that
\begin{equation}\label{eqn:qftLecture4:340}
[\partial_\mu \phi \partial^\mu \phi] = 5.
\end{equation}
A 5D Lagrangian could have local terms such as
\begin{equation}\label{eqn:qftLecture4:360}
\LL = \partial_\mu \phi \partial^\mu \phi + m^2 \phi^2 + \sqrt{\mu} \phi^3 + \inv{\mu’} \phi^4.
\end{equation}
where \( m, \mu, \mu’ \) all have mass dimensions. In 5D there are no marginal couplings. Dimension 4 is the last dimension where marginal couplings exist. In condensed matter physics 4D is called the “upper critical dimension”.
From the point of view of particle physics, all the terms in the Lagrangian must be the ones that are relevant at long distances.
Least action principle (classical field theory).
Now we want to study 4D scalar theories. We have some action
\begin{equation}\label{eqn:qftLecture4:380}
S[\phi] = \int d^4 x \LL(\phi, \partial_\mu \phi).
\end{equation}
Let’s keep an example such as the following in mind
\begin{equation}\label{eqn:qftLecture4:400}
\LL = \underbrace{\inv{2} \partial_\mu \phi \partial^\mu \phi}_{\text{Kinetic term}} – \underbrace{m^2 \phi – \lambda \phi^4}_{\text{all relevant and marginal couplings}}.
\end{equation}
The even powers can be justified by assuming there is some symmetry that kills the odd powered terms.
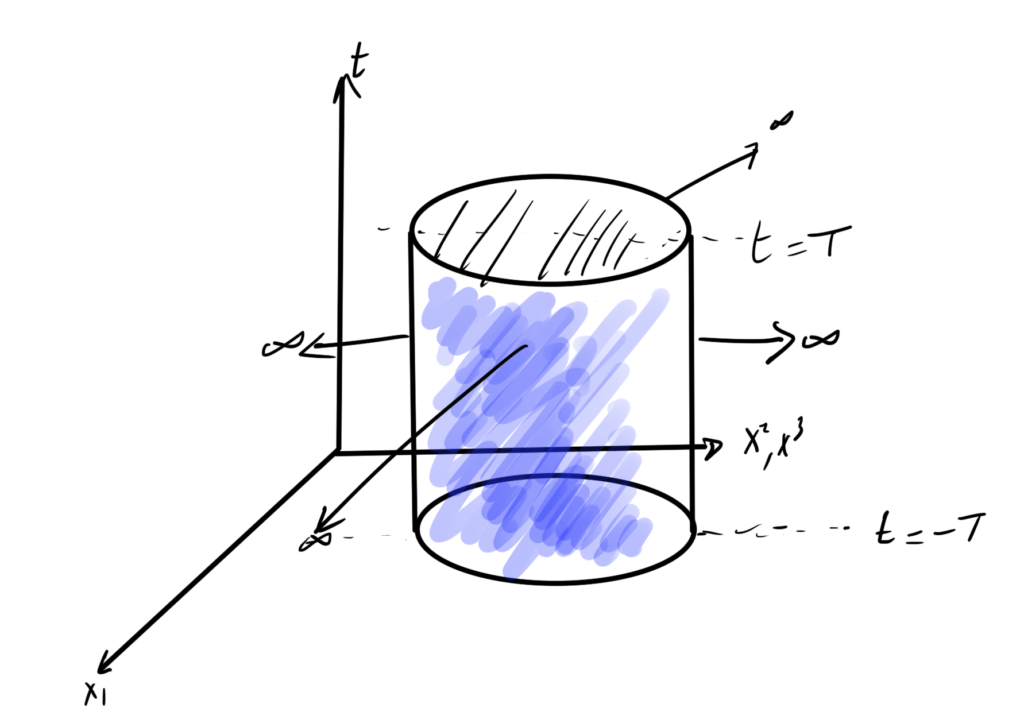
We will be integrating over a space time region such as that depicted in fig. 1, where a cylindrical spatial cross section is depicted that we allow to tend towards infinity. We demand that the field is fixed on the infinite spatial boundaries. The easiest way to demand that the field dies off on the spatial boundaries, that is
\begin{equation}\label{eqn:qftLecture4:420}
\lim_{\Abs{\Bx} \rightarrow \infty} \phi(\Bx) \rightarrow 0.
\end{equation}
The functional \( \phi(\Bx, t) \) that obeys the boundary condition as stated extremizes \( S[\phi] \).
Extremizing the action means that we seek \( \phi(\Bx, t) \)
\begin{equation}\label{eqn:qftLecture4:440}
\delta S[\phi] = 0 = S[\phi + \delta \phi] – S[\phi].
\end{equation}
How do we compute the variation?
\begin{equation}\label{eqn:qftLecture4:460}
\begin{aligned}
\delta S
&= \int d^d x \lr{ \LL(\phi + \delta \phi, \partial_\mu \phi + \partial_\mu \delta \phi) – \LL(\phi, \partial_\mu \phi) } \\
&= \int d^d x \lr{ \PD{\phi}{\LL} \delta \phi + \PD{(\partial_mu \phi)}{\LL} (\partial_\mu \delta \phi) } \\
&= \int d^d x \lr{ \PD{\phi}{\LL} \delta \phi
+ \partial_\mu \lr{ \PD{(\partial_mu \phi)}{\LL} \delta \phi}
– \lr{ \partial_\mu \PD{(\partial_mu \phi)}{\LL} } \delta \phi
} \\
&=
\int d^d x
\delta \phi
\lr{ \PD{\phi}{\LL}
– \partial_\mu \PD{(\partial_mu \phi)}{\LL} }
+ \int d^3 \sigma_\mu \lr{ \PD{(\partial_\mu \phi)}{\LL} \delta \phi }
\end{aligned}
\end{equation}
If we are explicit about the boundary term, we write it as
\begin{equation}\label{eqn:qftLecture4:480}
\int dt d^3 \Bx \partial_t \lr{ \PD{(\partial_t \phi)}{\LL} \delta \phi }
– \spacegrad \cdot \lr{ \PD{(\spacegrad \phi)}{\LL} \delta \phi }
=
\int d^3 \Bx \evalrange{ \PD{(\partial_t \phi)}{\LL} \delta \phi }{t = -T}{t = T}
– \int dt d^2 \BS \cdot \lr{ \PD{(\spacegrad \phi)}{\LL} \delta \phi }.
\end{equation}
but \( \delta \phi = 0 \) at \( t = \pm T \) and also at the spatial boundaries of the integration region.
This leaves
\begin{equation}\label{eqn:qftLecture4:500}
\delta S[\phi] = \int d^d x \delta \phi
\lr{ \PD{\phi}{\LL} – \partial_\mu \PD{(\partial_mu \phi)}{\LL} } = 0 \forall \delta \phi.
\end{equation}
That is
\begin{equation}\label{eqn:qftLecture4:540}
\boxed{
\PD{\phi}{\LL} – \partial_\mu \PD{(\partial_mu \phi)}{\LL} = 0.
}
\end{equation}
This are the Euler-Lagrange equations for a single scalar field.
Returning to our sample scalar Lagrangian
\begin{equation}\label{eqn:qftLecture4:560}
\LL = \inv{2} \partial_\mu \phi \partial^\mu \phi – \inv{2} m^2 \phi^2 – \frac{\lambda}{4} \phi^4.
\end{equation}
This example is related to the Ising model which has a \( \phi \rightarrow -\phi \) symmetry. Applying the Euler-Lagrange equations, we have
\begin{equation}\label{eqn:qftLecture4:580}
\PD{\phi}{\LL} = -m^2 \phi – \lambda \phi^3,
\end{equation}
and
\begin{equation}\label{eqn:qftLecture4:600}
\begin{aligned}
\PD{(\partial_\mu \phi)}{\LL}
&=
\PD{(\partial_\mu \phi)}{} \lr{
\inv{2} \partial_\nu \phi \partial^\nu \phi } \\
&=
\inv{2} \partial^\nu \phi
\PD{(\partial_\mu \phi)}{}
\partial_\nu \phi
+
\inv{2} \partial_\nu \phi
\PD{(\partial_\mu \phi)}{}
\partial_\alpha \phi g^{\nu\alpha} \\
&=
\inv{2} \partial^\mu \phi
+
\inv{2} \partial_\nu \phi g^{\nu\mu} \\
&=
\partial^\mu \phi
\end{aligned}
\end{equation}
so we have
\begin{equation}\label{eqn:qftLecture4:620}
\begin{aligned}
0
&=
\PD{\phi}{\LL} -\partial_\mu
\PD{(\partial_\mu \phi)}{\LL} \\
&=
-m^2 \phi – \lambda \phi^3 – \partial_\mu \partial^\mu \phi.
\end{aligned}
\end{equation}
For \( \lambda = 0 \), the free field theory limit, this is just
\begin{equation}\label{eqn:qftLecture4:640}
\partial_\mu \partial^\mu \phi + m^2 \phi = 0.
\end{equation}
Written out from the observer frame, this is
\begin{equation}\label{eqn:qftLecture4:660}
(\partial_t)^2 \phi – \spacegrad^2 \phi + m^2 \phi = 0.
\end{equation}
With a non-zero mass term
\begin{equation}\label{eqn:qftLecture4:680}
\lr{ \partial_t^2 – \spacegrad^2 + m^2 } \phi = 0,
\end{equation}
is called the Klein-Gordan equation.
If we also had \( m = 0 \) we’d have
\begin{equation}\label{eqn:qftLecture4:700}
\lr{ \partial_t^2 – \spacegrad^2 } \phi = 0,
\end{equation}
which is the wave equation (for a massless free field). This is also called the D’Alembert equation, which is familiar from electromagnetism where we have
\begin{equation}\label{eqn:qftLecture4:720}
\begin{aligned}
\lr{ \partial_t^2 – \spacegrad^2 } \BE &= 0 \\
\lr{ \partial_t^2 – \spacegrad^2 } \BB &= 0,
\end{aligned}
\end{equation}
in a source free region.
Canonical quantization.
\begin{equation}\label{eqn:qftLecture4:740}
\LL = \inv{2} \dot{q} – \frac{\omega^2}{2} q^2
\end{equation}
This has solution \(\ddot{q} = – \omega^2 q\).
Let
\begin{equation}\label{eqn:qftLecture4:760}
p = \PD{\dot{q}}{\LL} = \dot{q}
\end{equation}
\begin{equation}\label{eqn:qftLecture4:780}
H(p,q) = \evalbar{p \dot{q} – \LL}{\dot{q}(p, q)}
= p p – \inv{2} p^2 + \frac{\omega^2}{2} q^2 = \frac{p^2}{2} + \frac{\omega^2}{2} q^2
\end{equation}
In QM we quantize by mapping Poisson brackets to commutators.
\begin{equation}\label{eqn:qftLecture4:800}
\antisymmetric{\hatp}{\hat{q}} = -i
\end{equation}
One way to represent is to say that states are \( \Psi(\hat{q}) \), a wave function, \( \hat{q} \) acts by \( q \)
\begin{equation}\label{eqn:qftLecture4:820}
\hat{q} \Psi = q \Psi(q)
\end{equation}
With
\begin{equation}\label{eqn:qftLecture4:840}
\hatp = -i \PD{q}{},
\end{equation}
so
\begin{equation}\label{eqn:qftLecture4:860}
\antisymmetric{ -i \PD{q}{} } { q} = -i
\end{equation}
Let’s introduce an explicit space time split. We’ll write
\begin{equation}\label{eqn:qftLecture4:880}
L = \int d^3 x \lr{
\inv{2} (\partial_0 \phi(\Bx, t))^2 – \inv{2} \lr{ \spacegrad \phi(\Bx, t) }^2 – \frac{m^2}{2} \phi
},
\end{equation}
so that the action is
\begin{equation}\label{eqn:qftLecture4:900}
S = \int dt L.
\end{equation}
The dynamical variables are \( \phi(\Bx) \). We define
\begin{equation}\label{eqn:qftLecture4:920}
\begin{aligned}
\pi(\Bx, t) = \frac{\delta L}{\delta (\partial_0 \phi(\Bx, t))}
&=
\partial_0 \phi(\Bx, t) \\
&=
\dot{\phi}(\Bx, t),
\end{aligned}
\end{equation}
called the canonical momentum, or the momentum conjugate to \( \phi(\Bx, t) \). Why \( \delta \)? Has to do with an implicit Dirac function to eliminate the integral?
\begin{equation}\label{eqn:qftLecture4:940}
\begin{aligned}
H
&= \int d^3 x \evalbar{\lr{ \pi(\bar{\Bx}, t) \dot{\phi}(\bar{\Bx}, t) – L }}{\dot{\phi}(\bar{\Bx}, t) = \pi(x, t) } \\
&= \int d^3 x \lr{ (\pi(\Bx, t))^2 – \inv{2} (\pi(\Bx, t))^2 + \inv{2} (\spacegrad \phi)^2 + \frac{m}{2} \phi^2 },
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:qftLecture4:960}
H
= \int d^3 x \lr{ \inv{2} (\pi(\Bx, t))^2 + \inv{2} (\spacegrad \phi(\Bx, t))^2 + \frac{m}{2} (\phi(\Bx, t))^2 }
\end{equation}
In analogy to the momentum, position commutator in QM
\begin{equation}\label{eqn:qftLecture4:1000}
\antisymmetric{\hat{p}_i}{\hat{q}_j} = -i \delta_{ij},
\end{equation}
we “quantize” the scalar field theory by promoting \( \pi, \phi \) to operators and insisting that they also obey a commutator relationship
\begin{equation}\label{eqn:qftLecture4:980}
\antisymmetric{\pi(\Bx, t)}{\phi(\By, t)} = -i \delta^3(\Bx – \By).
\end{equation}
References
[1] Frank Wilczek. Fundamental constants. arXiv preprint arXiv:0708.4361, 2007. URL https://arxiv.org/abs/0708.4361.