[Click here for a PDF of this post with nicer formatting]
These are notes for the UofT course ECE1229, Advanced Antenna Theory, taught by Prof. Eleftheriades, covering ch. 4 [1] content.
Unlike most of the other classes I have taken, I am not attempting to take comprehensive notes for this class. The class is taught on slides that match the textbook so closely, there is little value to me taking notes that just replicate the text. Instead, I am annotating my copy of textbook with little details instead. My usual notes collection for the class will contain musings of details that were unclear, or in some cases, details that were provided in class, but are not in the text (and too long to pencil into my book.)
Magnetic Vector Potential.
In class and in the problem set \( \BA \) was referred to as the Magnetic Vector Potential. I only recalled this referred to as the Vector Potential. Prefixing this with magnetic seemed counter intuitive to me since it is generated by electric sources (charges and currents).
This terminology can be justified due to the fact that \( \BA \) generates the magnetic field by its curl. Some mention of this can be found in [4], which also points out that the Electric Potential refers to the scalar \( \phi \). Prof. Eleftheriades points out that Electric Vector Potential refers to the vector potential \( \BF \) generated by magnetic sources (because in that case the electric field is generated by the curl of \( \BF \).)
Plots of infinitesimal dipole radial dependence.
In section 4.2 of [1] are some discussions of the \( kr < 1 \), \( kr = 1 \), and \( kr > 1 \) radial dependence of the fields and power of a solution to an infinitesimal dipole system. Here are some plots of those \( k r \) dependence, along with the \( k r = 1 \) contour as a reference. All the \( \theta \) dependence and any scaling is left out.
The CDF notebook visualizeDipoleFields.cdf is available to interactively plot these, rotate the plots and change the ranges of what is plotted.
A plot of the real and imaginary parts of \( H_\phi = \frac{j k}{r} e^{-j k r} \lr{ 1-\frac{j}{k r} } \) can be found in fig. 1 and fig. 2.
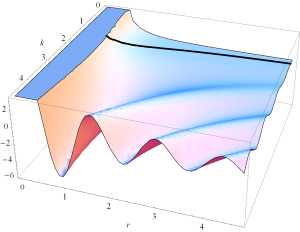
fig 1. Radial dependence of Re H_phi
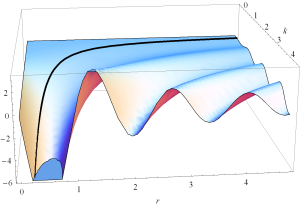
fig 2. Radial dependence of Im H_phi
A plot of the real and imaginary parts of \( E_r = \inv{r^2} \lr{1-\frac{j}{k r}} e^{-j k r} \) can be found in fig. 3 and fig. 4.
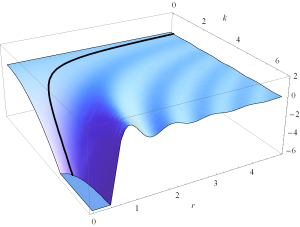
fig 3. Radial dependence of Re E_r
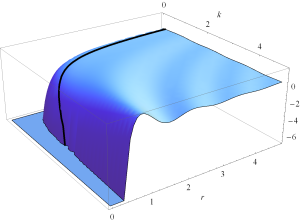
fig 4. Radial dependence of Im E_r
Finally, a plot of the real and imaginary parts of \( E_\theta = \frac{ j k }{r} \lr{1 -\frac{j}{k r} -\frac{1}{k^2 r^2} } e^{-j k r} \) can be found in fig. 5 and fig. 6.
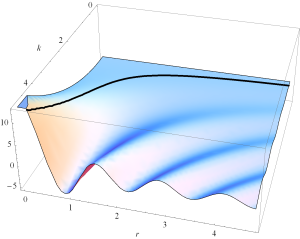
fig. 5. Radial dependence of Re E_theta

fig. 6. Radial dependence of Im E_theta
Electric Far field for a spherical potential.
It is interesting to look at the far electric field associated with an arbitrary spherical magnetic vector potential, assuming all of the radial dependence is in the spherical envelope. That is
\begin{equation}\label{eqn:chapter4Notes:20}
\BA = \frac{e^{-j k r}}{r} \lr{
\rcap a_r\lr{ \theta, \phi }
+\thetacap a_\theta\lr{ \theta, \phi }
+\phicap a_\phi\lr{ \theta, \phi }
}.
\end{equation}
The electric field is
\begin{equation}\label{eqn:chapter4Notes:40}
\BE = – j \omega \BA – j \frac{1}{\omega \mu_0 \epsilon_0 } \spacegrad \lr{\spacegrad \cdot \BA }.
\end{equation}
The divergence and gradient in spherical coordinates are
\begin{equation}\label{eqn:chapter4Notes:80}
\begin{aligned}
\spacegrad \cdot \BA
&=
\inv{r^2} \PD{r}{} \lr{ r^2 A_r }
+ \inv{r \sin\theta } \PD{\theta}{} \lr{A_\theta \sin\theta}
+ \inv{r \sin\theta } \PD{\phi}{A_\phi}
\end{aligned}
\end{equation}
\begin{equation}\label{eqn:chapter4Notes:100}
\begin{aligned}
\spacegrad \psi \\
&=
\rcap \PD{r}{\psi}
+\frac{\thetacap}{r} \PD{\theta}{\psi}
+ \frac{\phicap}{r \sin\theta} \PD{\phi}{\psi}.
\end{aligned}
\end{equation}
For the assumed potential, the divergence is
\begin{equation}\label{eqn:chapter4Notes:120}
\begin{aligned}
\spacegrad \cdot \BA
&=
\frac{a_r}{r^2} \PD{r}{} \lr{ r^2 \frac{e^{-j k r}}{r} }
+ \inv{r \sin\theta } \frac{e^{-j k r}}{r} \PD{\theta}{} \lr{\sin\theta a_\theta}
+ \inv{r \sin\theta } \frac{e^{-j k r}}{r} \PD{\phi}{a_\phi} \\
&=
a_r
e^{-j k r}
\lr{
\inv{r^2}
-j k \inv{r}
}
+ \inv{r^2 \sin\theta } e^{-j k r} \PD{\theta}{} \lr{\sin\theta a_\theta}
+ \inv{r^2 \sin\theta } e^{-j k r} \PD{\phi}{a_\phi} \\
&\approx
-j k \frac{a_r}{r}
e^{-j k r}.
\end{aligned}
\end{equation}
The last approximation dropped all the \( 1/r^2 \) terms that will be small compared to \( 1/r \) contribution that dominates when \( r \rightarrow \infty \), the far field.
The gradient can now be computed
\begin{equation}\label{eqn:chapter4Notes:140}
\begin{aligned}
\spacegrad \lr{\spacegrad \cdot \BA }
&\approx
-j k
\spacegrad
\lr{
\frac{a_r}{r}
e^{-j k r}
} \\
&=
-j k \lr{
\rcap \PD{r}{}
+\frac{\thetacap}{r} \PD{\theta}{}
+ \frac{\phicap}{r \sin\theta} \PD{\phi}{}
}
\frac{a_r}{r}
e^{-j k r} \\
&=
-j k \lr{
\rcap a_r \PD{r}{} \lr{
\frac{1}{r}
e^{-j k r}
}
+\frac{\thetacap}{r^2}
e^{-j k r}
\PD{\theta}{a_r}
+
e^{-j k r}
\frac{\phicap}{r^2 \sin\theta}
\PD{\phi}{a_r}
} \\
&=
-j k \lr{
-\rcap \frac{a_r}{r^2} \lr{
1
+ j k r
}
+\frac{\thetacap}{r^2}
\PD{\theta}{a_r}
+
\frac{\phicap}{r^2 \sin\theta}
\PD{\phi}{a_r}
}
e^{-j k r} \\
&\approx
– k^2 \rcap \frac{a_r}{r}
e^{-j k r}.
\end{aligned}
\end{equation}
Again, a far field approximation has been used to kill all the \( 1/r^2 \) terms.
The far field approximation of the electric field is now possible
\begin{equation}\label{eqn:chapter4Notes:160}
\begin{aligned}
\BE
&= – j \omega \BA – j \frac{1}{\omega \mu_0 \epsilon_0 } \spacegrad \lr{\spacegrad \cdot \BA } \\
&=
– j \omega
\frac{e^{-j k r}}{r} \lr{
\rcap a_r\lr{ \theta, \phi }
+\thetacap a_\theta\lr{ \theta, \phi }
+\phicap a_\phi\lr{ \theta, \phi }
}
+ j \frac{1}{\omega \mu_0 \epsilon_0 }
k^2 \rcap \frac{a_r}{r}
e^{-j k r} \\
&=
– j \omega
\frac{e^{-j k r}}{r} \lr{
\rcap a_r\lr{ \theta, \phi }
+\thetacap a_\theta\lr{ \theta, \phi }
+\phicap a_\phi\lr{ \theta, \phi }
}
+ j \frac{c^2}{\omega }
\lr{\frac{\omega}{c}}^2 \rcap \frac{a_r}{r}
e^{-j k r}
\\
&=
– j \omega
\frac{e^{-j k r}}{r} \lr{
\thetacap a_\theta\lr{ \theta, \phi }
+\phicap a_\phi\lr{ \theta, \phi }
}.
\end{aligned}
\end{equation}
Observe the perfect, somewhat miraculous seeming, cancellation of all the radial components of the field. If \( \BA_{\textrm{T}} \) is the non-radial projection of \( \BA \), the electric far field is just
\begin{equation}\label{eqn:chapter4Notes:180}
\boxed{
\BE_{\textrm{ff}} = -j \omega \BA_{\textrm{T}}.
}
\end{equation}
Magnetic Far field for a spherical potential.
Application of the same assumed representation for the magnetic field gives
\begin{equation}\label{eqn:chapter4Notes:220}
\begin{aligned}
\BB
&=
\spacegrad \cross \BA \\
&=
\frac{\rcap}{r \sin\theta} \partial_\theta \lr{A_\phi \sin\theta}
+ \frac{\thetacap}{r} \lr{ \inv{\sin\theta} \partial_\phi A_r – \partial_r \lr{r A_\phi}}
+ \frac{\phicap}{r} \lr{ \partial_r\lr{r A_\theta} – \partial_\theta A_r} \\
&=
\frac{\rcap}{r \sin\theta} \partial_\theta \lr{
\frac{e^{-j k r}}{r} a_\phi
\sin\theta}
+ \frac{\thetacap}{r} \lr{ \inv{\sin\theta} \partial_\phi \lr{
\frac{e^{-j k r}}{r} a_r
} – \partial_r \lr{r
\frac{e^{-j k r}}{r} a_\phi
}
}
+ \frac{\phicap}{r} \lr{ \partial_r\lr{r
\frac{e^{-j k r}}{r} a_\theta
} – \partial_\theta
\lr{
\frac{e^{-j k r}}{r} a_r
}
} \\
&=
\frac{\rcap}{r \sin\theta}
\frac{e^{-j k r}}{r}
\partial_\theta \lr{
a_\phi
\sin\theta}
+ \frac{\thetacap}{r} \lr{ \inv{\sin\theta}
\frac{e^{-j k r}}{r}
\partial_\phi
a_r
– \partial_r \lr{
e^{-j k r}
}
a_\phi
}
+ \frac{\phicap}{r} \lr{
\partial_r
\lr{
e^{-j k r}
}
a_\theta
–
\frac{e^{-j k r}}{r}
\partial_\theta
a_r
}
\approx
j k \lr{ \thetacap a_\phi
–
\phicap a_\theta
}
\frac{e^{-j k r}}{r} \\
&=
-j k \rcap \cross \lr{
\thetacap a_\theta
+\phicap a_\phi
}
\frac{e^{-j k r}}{r} \\
&=
\inv{c} \BE_{\textrm{ff}}.
\end{aligned}
\end{equation}
The approximation above drops the \( 1/r^2 \) terms. Since
\begin{equation}\label{eqn:chapter4Notes:240}
\inv{\mu_0 c} = \inv{\mu_0} \sqrt{\mu_0\epsilon_0} = \sqrt{\frac{\epsilon_0}{\mu_0}} = \inv{\eta},
\end{equation}
the magnetic far field can be expressed in terms of the electric far field as
\begin{equation}\label{eqn:chapter4Notes:260}
\boxed{
\BH = \inv{\eta} \rcap \cross \BE.
}
\end{equation}
Plane wave relations between electric and magnetic fields
I recalled an identity of the form \ref{eqn:chapter4Notes:260} in [3], but didn’t think that it required a far field approximation.
The reason for this was because the Jackson identity assumed a plane wave representation of the field, something that the far field assumptions also locally require.
Assuming a plane wave representation for both fields
\begin{equation}\label{eqn:chapter4Notes:300}
\boldsymbol{\mathcal{E}}(\Bx, t) = \BE e^{j \lr{\omega t – \Bk \cdot \Bx}}
\end{equation}
\begin{equation}\label{eqn:chapter4Notes:320}
\boldsymbol{\mathcal{B}}(\Bx, t) = \BB e^{j \lr{\omega t – \Bk \cdot \Bx}}
\end{equation}
The cross product relation between the fields follows from the Maxwell-Faraday law of induction
\begin{equation}\label{eqn:chapter4Notes:340}
0 = \spacegrad \cross \boldsymbol{\mathcal{E}} + \PD{t}{\boldsymbol{\mathcal{B}}},
\end{equation}
or
\begin{equation}\label{eqn:chapter4Notes:360}
\begin{aligned}
0
&=
\Be_r \cross \BE \partial_r e^{j\lr{ \omega t – \Bk \cdot \Bx}}
+
j \omega \BB e^{j \lr{\omega t – \Bk \cdot \Bx}} \\
&=
-j \Be_r k_r \cross \BE e^{j \lr{\omega t – \Bk \cdot \Bx}}
+
j \omega \BB e^{j \lr{\omega t – \Bk \cdot \Bx}} \\
&=
\lr{ – \Bk \cross \BE + \omega \BB } j
e^{j \lr{\omega t – \Bk \cdot \Bx}},
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:chapter4Notes:380}
\begin{aligned}
\BH
&= \frac{ k}{k c \mu_0 } \kcap \cross \BE \\
&= \inv{ \eta } \kcap \cross \BE,
\end{aligned}
\end{equation}
which also finds \ref{eqn:chapter4Notes:260}, but with much less work and less mess.
Transverse only nature of the far-field fields
Also observe that its possible to tell that the far field fields have only transverse components using the same argument that they are locally plane waves at that distance. The plane waves must satisfy the zero divergence Maxwell’s equations
\begin{equation}\label{eqn:chapter4Notes:420}
\spacegrad \cdot \boldsymbol{\mathcal{E}} = 0
\end{equation}
\begin{equation}\label{eqn:chapter4Notes:440}
\spacegrad \cdot \boldsymbol{\mathcal{B}} = 0,
\end{equation}
so by the same logic
\begin{equation}\label{eqn:chapter4Notes:480}
\Bk \cdot \BE = 0
\end{equation}
\begin{equation}\label{eqn:chapter4Notes:500}
\Bk \cdot \BB = 0.
\end{equation}
In the far field the electric field must equal its transverse projection
\begin{equation}\label{eqn:chapter4Notes:520}
\BE = \textrm{Proj}_\T \lr{-j \omega \BA
– j \frac{1}{\omega \mu_0 \epsilon_0 } \spacegrad \lr{\spacegrad \cdot \BA } }.
\end{equation}
Since by \ref{eqn:chapter4Notes:140} the scalar potential term has only a radial component, that leaves
\begin{equation}\label{eqn:chapter4Notes:540}
\BE = -j \omega \textrm{Proj}_\T \BA,
\end{equation}
which provides \ref{eqn:chapter4Notes:180} with slightly less work.
Vertical dipole reflection coefficient
In class a ground reflection scenario was covered for a horizontal dipole. Reading the text I was surprised to see what looked like the same sort of treatment section 4.7.2, but ending up with a quite different result. It turns out the difference is because the text was treating the vertical dipole configuration, whereas Prof. Eleftheriades was treating a horizontal dipole configuration, which have different reflection coefficients. These differing reflection coefficients are due to differences in the polarization of the field.
To understand these differences in reflection coefficients, consider first the field due to a vertical dipole as sketched in fig. 7, with a wave vector directed from the transmission point downwards in the z-y plane.
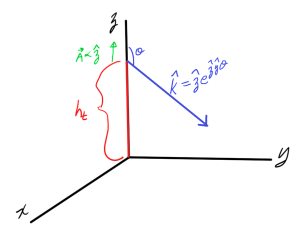
fig. 7. vertical dipole configuration.
The wave vector has direction
\begin{equation}\label{eqn:chapter4Notes:560}
\kcap = \zcap e^{\zcap \xcap \theta} = \zcap \cos\theta + \ycap \sin\theta.
\end{equation}
Suppose that the (magnetic) vector potential is that of an infinitesimal dipole
\begin{equation}\label{eqn:chapter4Notes:580}
\BA = \zcap \frac{\mu_0 I_0 l}{4 \pi r} e^{-j k r} %= \frac{A_r}{4 \pi r} e^{-j k r}
\end{equation}
The electric field, in the far field, can be computed by computing the normal projection to the wave vector direction
\begin{equation}\label{eqn:chapter4Notes:600}
\begin{aligned}
\BE
&= -j \omega \lr{\BA \wedge \kcap} \cdot \kcap \\
&= -j \omega \frac{\mu_0 I_0 l}{4 \pi r} \lr{\zcap \wedge \lr{\zcap \cos\theta
+ \ycap \sin\theta} } \lr{\zcap \cos\theta + \ycap \sin\theta} \\
&= -j \omega \frac{\mu_0 I_0 l}{4 \pi r} \lr{ \zcap \ycap \sin\theta }
\lr{\zcap \cos\theta + \ycap \sin\theta} \\
&= -j \omega \frac{\mu_0 I_0 l}{4 \pi r} \sin\theta \lr{-\ycap \cos\theta +
\zcap \sin\theta} \\
&= j \omega \frac{\mu_0 I_0 l}{4 \pi r} \sin\theta \ycap e^{\zcap \ycap \theta}.
\end{aligned}
\end{equation}
This is directed in the z-y plane rotated an additional \( \pi/2 \) past \( \kcap \). The magnetic field must then be directed into the page, along the x axis. This is sketched in fig. 8.
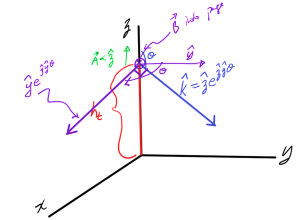
fig. 8. Electric and magnetic field directions
Referring to [2] (\eqntext 4.40) for the coefficient of reflection component
\begin{equation}\label{eqn:chapter4Notes:620}
R
=
\frac{
n_t \cos\theta_i – n_i \cos\theta_t
}
{
n_i \cos\theta_i + n_t \cos\theta_t
}
\end{equation}
This is the Fresnel equation for the case when
that corresponds to
\( \BE \) lies in the plane of incidence, and the magnetic field is completely parallel to the plane of reflection). For the no transmission case, allowing \( v_t \rightarrow 0 \), the index of refraction is \( n_t = c/v_t \rightarrow \infty \), and the reflection coefficient is \( 1 \) as claimed in section 4.7.2 of [1]. Because of the symmetry of this dipole configuration, the azimuthal angle that the wave vector is directed along does not matter.
Horizontal dipole reflection coefficient
In the class notes, a horizontal dipole coming out of the page is indicated. With the page representing the z-y plane, this is a magnetic vector potential directed along the x-axis direction
\begin{equation}\label{eqn:chapter4Notes:640}
\BA = \xcap \frac{\mu_0 I_0 l}{4 \pi r} e^{-j k r}.
\end{equation}
For a wave vector directed in the z-y plane as in \ref{eqn:chapter4Notes:560}, the electric far field is directed along
\begin{equation}\label{eqn:chapter4Notes:660}
\begin{aligned}
\lr{ \xcap \wedge \kcap } \cdot \kcap
&=
\xcap – \lr{ \xcap \cdot \kcap } \kcap \\
&=
\xcap – \lr{ \xcap \cdot \lr{
\zcap \cos\theta + \ycap \sin\theta
} } \kcap \\
&= \xcap.
\end{aligned}
\end{equation}
The electric far field lies completely in the plane of reflection. From [2] (\eqntext 4.34), the Fresnel reflection coefficients is
\begin{equation}\label{eqn:chapter4Notes:680}
R =
\frac{
n_i \cos\theta_i – n_t \cos\theta_t
}
{
n_i \cos\theta_i + n_t \cos\theta_t
},
\end{equation}
which approaches \( -1 \) when \( n_t \rightarrow \infty \). This is consistent with the image theorem summation that Prof. Eleftheriades used in class.
Azimuthal angle dependency of the reflection coefficient
Now consider a horizontal dipole directed along the y-axis. For the same wave vector direction as avove, the electric far field is now directed along
\begin{equation}\label{eqn:chapter4Notes:700}
\begin{aligned}
\lr{ \ycap \wedge \kcap } \cdot \kcap
&=
\ycap – \lr{ \ycap \cdot \kcap } \kcap \\
&=
\ycap – \lr{ \ycap \cdot \lr{
\zcap \cos\theta + \ycap \sin\theta
} } \kcap \\
&=
\ycap – \kcap \sin\theta \\
&=
\ycap – \sin\theta \lr{
\zcap \cos\theta + \ycap \sin\theta
} \\
&=
\ycap \cos^2 \theta – \sin\theta \cos\theta \zcap \\
&= \cos\theta \lr{ \ycap \cos\theta – \sin\theta \zcap } \\
&= \cos\theta \ycap e^{ \zcap \ycap \theta }.
\end{aligned}
\end{equation}
That is
\begin{equation}\label{eqn:chapter4Notes:720}
\BE =
-j \omega \frac{\mu_0 I_0 l}{4 \pi r} e^{-j k r}
\cos\theta \ycap e^{ \zcap \ycap \theta }.
\end{equation}
This far field electric field lies in the plane of incidence (a direction of \( \thetacap \) rotated by \( \pi/2 \)), not in the plane of reflection. The corresponding magnetic field should be directed along the plane of reflection, which is easily confirmed by calculation
\begin{equation}\label{eqn:chapter4Notes:740}
\begin{aligned}
\kcap \cross
\lr{ \ycap \cos\theta – \sin\theta \zcap }
&=
\lr{ \zcap \cos\theta + \ycap \sin\theta } \cross
\lr{ \ycap \cos\theta – \sin\theta \zcap } \\
&=
-\xcap \cos^2 \theta – \xcap \sin^2\theta \\
&= -\xcap.
\end{aligned}
\end{equation}
The far field magnetic field is seen to be
\begin{equation}\label{eqn:chapter4Notes:721}
\BH =
j \omega \frac{I_0 l}{4 \pi r} e^{-j k r}
\cos\theta \xcap,
\end{equation}
so a reflection coefficient of \( 1 \) is required to calculate the power loss after a single ground reflection signal bounce for this relative orientation of antenna to the target.
I fail to see how the horizontal dipole treatment in section 4.7.5 can use a single reflection coefficient without taking into account the azimuthal dependency of that reflection coefficient.
References
[1] Constantine A Balanis. Antenna theory: analysis and design. John Wiley \& Sons, 3rd edition, 2005.
[2] E. Hecht. Optics. 1998.
[3] JD Jackson. Classical Electrodynamics. John Wiley and Sons, 2nd edition, 1975.
[4] Wikipedia. Magnetic potential — Wikipedia, The Free Encyclopedia, 2015. URL https://en.wikipedia.org/w/index.php?title=Magnetic_potential&oldid=642387563. [Online; accessed 5-February-2015].
Like this:
Like Loading...








