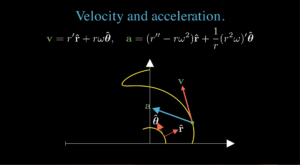
In this video, we compute velocity in a radial representation \( \mathbf{x} = r \mathbf{\hat{r}} \).
We use a scalar radial coordinate \( r \), and leave all the angular dependence implicitly encoded in a radial unit vector \( \mathbf{\hat{r}} \).
We find the geometric algebra structure of the \( \mathbf{\hat{r}}’ \) in two different ways, to find
\( \mathbf{\hat{r}}’ = \frac{\mathbf{\hat{r}}}{r} \left( \mathbf{\hat{r}} \wedge \mathbf{\hat{x}}’ \right), \)
then derive the conventional triple vector cross product equivalent for reference:
\( \mathbf{\hat{r}}’ = \left( \mathbf{\hat{r}} \times \mathbf{\hat{x}}’ \right) \times \frac{\mathbf{\hat{r}}}{r}. \)
We then compute kinetic energy in this representation, and show how a bivector-valued angular momentum \( L = \mathbf{x} \wedge \mathbf{p} \), falls naturally from that computation, where we have
\( \frac{m}{2} \mathbf{v}^2 = \frac{1}{2 m} {(m r’)}^2 – \frac{1}{2 m r^2 } L^2. \)
Prerequisites: calculus (derivatives and chain rule), and geometric algebra basics (vector multiplication, commutation relationships for vectors and bivectors in a plane, wedge and cross product equivalencies, …)
Errata: at around 4:12 I used \( \mathbf{r} \) instead of \( \mathbf{x} \), then kept doing so every time after that when the value for \( L \) was stated.
As well as being posted to Google’s censorship-tube, this video can also be found on odysee.