[Click here for a PDF version of this post]

I saw an interesting solution of an introductory programming source sample problem, showing how to display Pascal’s triangle up to a given size. For example, given input \( n = 5 \), the output should be like:
\begin{equation*}
\begin{array}{c}
1 \\
1 \quad 1 \\
1 \quad 2 \quad 1 \\
1 \quad 3 \quad 3 \quad 1 \\
1 \quad 4 \quad 6 \quad 4 \quad 1 \\
1 \quad 5 \quad 10 \quad 10 \quad 5 \quad 1
\end{array}
\end{equation*}

One kind of neat property of Pascal’s triangle is that any non-unity number on the triangle, is the sum of the two numbers above it. That’s one of the ways that I’d imagine a student would solve the programming problem of displaying this triangle.

Another way would be to use a formula for the binomial coefficients. Recall that

Theorem 1.1: Binomial theorem for integer powers.

These \( \binom{n}{k} \) values are the binomial coefficients, and are, in fact the values in Pascal’s triangle (we will show this in a bit.)

What surprised me about the programming solution that I saw was that it didn’t use the binomial coefficients. Instead if appeared to use a recurrence relationship, which was interesting, because I didn’t remember any such relationship. We’ll also find that recurrence relationship below, which allows for evaluation of the binomial coefficients without evaluating any of the factorials.

Combinatoric argument for the binomial coefficients

Let’s look at an explicit expansion of the LHS of the binomial theorem for the first few values of \( n \), starting at \(2\).
\begin{equation}\label{eqn:pascals:20}
\lr{ H + T }^2 = \lr{ H + T }\lr{ H + T} = H H + H T + T H + T T.
\end{equation}
We see that we have all possible combinations of \( H, T \) in the final expression, but because of assumed commutation, there is some redundancy, and we can write
\begin{equation}\label{eqn:pascals:40}
\lr{ H + T }^2 = H^2 + 2 H T + T T.
\end{equation}
If we enumerate all possible values for two flips of a coin, there can only be one \( H, H \) pair, there will be two \( H, T \) pairs, and one \( T, T \) pair. These numbers are the second row of Pascal’s triangle: \( 1, 2, 1 \).

Similarly, for \( n = 3 \), we have
\begin{equation}\label{eqn:pascals:60}
\begin{aligned}
\lr{ H + T }^3
&= \lr{ H H + H T + T H + T T } \lr{ H + T } \\
&= H H H + H T H + T H H + T T H + H H T + H T T + T H T + T T T.
\end{aligned}
\end{equation}
This time, after grouping, we have
\begin{equation}\label{eqn:pascals:80}
\lr{ H + T }^3 = H^3 + 3 H^2 T + 3 H T^2 + T^3.
\end{equation}
If we enumerate all possible values for three flips of a coin, there can only be one \( H, H, H \) triplet, there will be three \( H, H, T \) triplets, three \( T, T, H \) triplets, and one \( T, T, T \) triplet. These numbers are the third row of Pascal’s triangle: \( 1, 3, 3, 1 \).

To understand the binomial coefficient, we have to consider how to pick indistinguishable items from a set. Suppose that we want to pick three items from a set of 7, in a specific order. There are 7 ways to pick the first item, 6 ways to pick the second, and 5 ways to pick the third. We can express that as

\begin{equation}\label{eqn:pascals:120}
P(7,3) = 7 \times 6 \times 5 = \frac{7!}{4!} = \frac{7!}{\lr{7-3}!},
\end{equation}
or more generally, to pick \( k \) distinguishable items from a set of \( n \)
\begin{equation}\label{eqn:pascals:140}
P(n,k) = \frac{n!}{\lr{n-k}!}.
\end{equation}
In our \( \lr{H + T}^n \) expansion, we cannot distinguish any of the elements. For each \( k \) items we pick, there are \( k! \) ways of arranging those, so the binomial coefficient is
\begin{equation}\label{eqn:pascals:160}
\binom{n}{k} = \frac{P(n,k)}{k!} = \frac{n!}{k!\lr{n-k}!},
\end{equation}
as stated earlier.

Recurrence relation

For the recurrence relation, let’s assume that we have already found \( \binom{n}{k} \), let’s see if we can use that to find the next on the line. That is, for \( k < n \)
\begin{equation}\label{eqn:pascals:100}
\begin{aligned}
\binom{n}{k + 1}
&= \frac{n!}{\lr{k+1}!\lr{n-(k+1)}!} \\
&= \frac{n!}{\lr{k+1} k!\lr{n – k – 1)}!} \\
&= \frac{n! \lr{ n – k }}{\lr{k+1} k!\lr{n – k)}!} \\
&= \binom{n}{k} \frac{n – k}{k + 1}.
\end{aligned}
\end{equation}

This is a kind of cool result, and is the method that I saw used in the solution to the Pascal’s triangle program. We can start with the 1 value at the left of any row, and with a single multiply and divide, figure out the next entry in the triangle, and proceed from there.

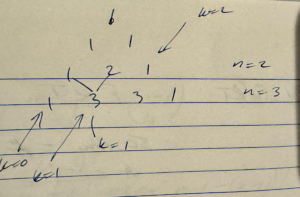
Pascal’s triangle.

For the Pascal’s triangle property to hold, we must have, for any \( k \ne 0 \)
\begin{equation}\label{eqn:pascals:180}
\binom{n}{k} = \binom{n-1}{k-1} + \binom{n-1}{k},
\end{equation}
as illustrated in fig. 1.

fig. 1. Pascal’s triangle, sum of elements above.

It’s fairly straightforward to verify that this property holds.
\begin{equation}\label{eqn:pascals:200}
\begin{aligned}
\binom{n-1}{k-1} + \binom{n-1}{k}
&=
\frac{\lr{n-1}!}{\lr{k-1}!\lr{n-1-\lr{k-1}}!}
+
\frac{\lr{n-1}!}{\lr{k}!\lr{n-1-k}!} \\
&=
\frac{\lr{n-1}!}{\lr{k-1}!} \lr{ \inv{\lr{n-k}!} + \inv{k \lr{n-1-k}!} } \\
&=
\frac{\lr{n-1}!}{\lr{k-1}!\lr{n-1-k}!} \lr{ \inv{n-k} + \inv{k} } \\
&=
\frac{\lr{n-1}!}{\lr{k-1}!\lr{n-1-k}!} \frac{k + n – k }{k \lr{ n – k } } \\
&=
\frac{n!}{k!\lr{n-k}!} \\
&=
\binom{n}{k},
\end{aligned}
\end{equation}
as expected.