Karl’s 1st year C programming course included IEEE floating point representation. It’s good to understand that representation, but pretty silly to try to do those conversions by hand.
I remember covering this in our computer organization course, but by that time I’d already figured it out for my own purposes. I wasn’t smart enough to look it up, and figured it out the hard way by reverse engineering the layout with printfs or the debugger or something like that.
I couldn’t help myself and wrote a little program to unpack a (32-bit) float into it’s representative parts. The idea is that we have a number in the form:
\begin{equation}\label{eqn:float32:1}
\pm 1.bbbbbbbb x 2^n
\end{equation}
The sizes of those components in a 32-bit C float type are:
- 1 sign bit,
- 8 exponent bits,
- 1 implied 1 mantissa bit,
- 23 mantissa bits,
where the exponent has a bias (127 = (1<<7)-1) so that the hardware doesn’t have to do any twos complement manipulation.
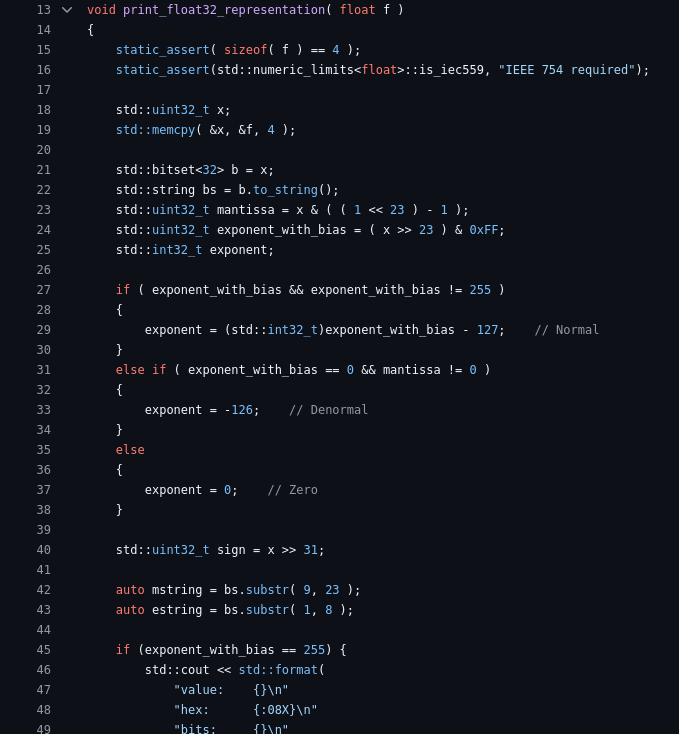
I’ve put my little floating point explorer program on github. Here is some sample output:
value: 0 hex: 00000000 bits: 00000000000000000000000000000000 sign: 0 exponent: 00000000 (0+0) mantissa: 00000000000000000000000 number: 0.00000000000000000000000 x 2^(0) value: inf hex: 7F800000 bits: 01111111100000000000000000000000 sign: 0 exponent: 11111111 mantissa: 00000000000000000000000 number: +inf value: -inf hex: FF800000 bits: 11111111100000000000000000000000 sign: 1 exponent: 11111111 mantissa: 00000000000000000000000 number: -inf value: nan hex: 7FC00000 bits: 01111111110000000000000000000000 sign: 0 exponent: 11111111 mantissa: 10000000000000000000000 number: NaN value: 1.1754944e-38 hex: 00800000 bits: 00000000100000000000000000000000 sign: 0 exponent: 00000001 (127 -126) mantissa: 00000000000000000000000 number: 1.00000000000000000000000 x 2^(-126) value: 3.4028235e+38 hex: 7F7FFFFF bits: 01111111011111111111111111111111 sign: 0 exponent: 11111110 (127 +127) mantissa: 11111111111111111111111 number: 1.11111111111111111111111 x 2^(127) Smallest denormal: value: 1e-45 hex: 00000001 bits: 00000000000000000000000000000001 sign: 0 exponent: 00000000 (0-126) mantissa: 00000000000000000000001 number: 0.00000000000000000000001 x 2^(-126) Largest denormal: value: 1.1754942e-38 hex: 007FFFFF bits: 00000000011111111111111111111111 sign: 0 exponent: 00000000 (0-126) mantissa: 11111111111111111111111 number: 0.11111111111111111111111 x 2^(-126) value: 1 hex: 3F800000 bits: 00111111100000000000000000000000 sign: 0 exponent: 01111111 (127 +0) mantissa: 00000000000000000000000 number: 1.00000000000000000000000 x 2^(0) value: -2 hex: C0000000 bits: 11000000000000000000000000000000 sign: 1 exponent: 10000000 (127 +1) mantissa: 00000000000000000000000 number: -1.00000000000000000000000 x 2^(1) value: 6 hex: 40C00000 bits: 01000000110000000000000000000000 sign: 0 exponent: 10000001 (127 +2) mantissa: 10000000000000000000000 number: 1.10000000000000000000000 x 2^(2) value: 1.5 hex: 3FC00000 bits: 00111111110000000000000000000000 sign: 0 exponent: 01111111 (127 +0) mantissa: 10000000000000000000000 number: 1.10000000000000000000000 x 2^(0) value: 0.125 hex: 3E000000 bits: 00111110000000000000000000000000 sign: 0 exponent: 01111100 (127 -3) mantissa: 00000000000000000000000 number: 1.00000000000000000000000 x 2^(-3)
Shoutout to Grok for the code review and the code fragments required to show the representation of NaN, \( \pm \infty \), and denormalized numbers. Grok offered to help extend this to double and long double representations, but where is the fun in letting it do that — that’s an exercise for another day.
codemore code
~~~~