[Click here for a PDF of this post with nicer formatting]
Motivation.
I have way too many Dover books on mathematics, including [1], which is a nice little book, covering all basics, plus some higher level material like gamma functions, Fourier series, and Laplace transforms. I’d borrowed this book from the Toronto Public Library in my youth. I’ve been meaning to re-read it, and bought my own copy to do so (too long ago.)
Perusing the chapter on vectors, I saw his treatment of lines, specifically the distance from a point to a line, and realized I’d left that elementary geometry topics out of my book.
Let’s tackle this and the similar distance from a plane problem here.
Distance from a line.
Given a point \( \Bx \) on a line, and a direction vector \( \Bu \) for the line, we can parameterize all points \( \By \) on the line by
\begin{equation}\label{eqn:lineAndPlane:20}
\By(t) = \Bx + a \Bu.
\end{equation}
In particular, the vector \( \Bx – \By \) is directed along the line if
\begin{equation}\label{eqn:lineAndPlane:40}
\lr{ \Bx – \By } \wedge \Bu = 0.
\end{equation}
While \ref{eqn:lineAndPlane:40} holds in \(\mathbb{R}^2\) (and in fact \(\mathbb{R}^N\)), this relationship is usually written in the \(\mathbb{R}^3\) specific dual form
\begin{equation}\label{eqn:lineAndPlane:60}
\lr{ \Bx – \By } \cross \Bu = 0.
\end{equation}
Given a vector \( \Bs \), representing a point, not necessarily on the line, we can compute the (shortest) distance from that point to the line.
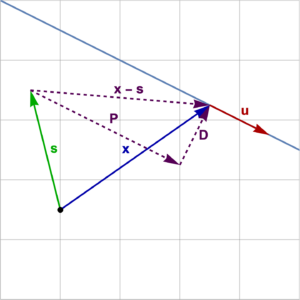
Fig 1. Distance to line.
Referring to fig. 1, it’s clear that we want this distance is just the rejection of \( \Bu \) from \( \Bd = \Bx – \Bs \). We can decompose \( \Bd \) into components parallel and perpendicular to \( \Bu \) using the usual trick
\begin{equation}\label{eqn:lineAndPlane:260}
\begin{aligned}
\Bd
&= \Bd \Bu \inv{\Bu} \\
&=
\lr{ \Bd \cdot \Bu }
\inv{\Bu}
+
\lr{ \Bd \wedge \Bu }
\inv{\Bu},
\end{aligned}
\end{equation}
where the first component is the projection along \( \Bu \), and the last is the rejection. This means that the
directed distance to the line from the point \( \Bs \) is
\begin{equation}\label{eqn:lineAndPlane:80}
\BD = \lr{\lr{\Bx – \Bs} \wedge \Bu } \inv{\Bu}.
\end{equation}
Should we want the conventional cross product formulation of this vector, this product may be expanded within a no-op grade-1 selection, applying the duality relation (\(\Bx \wedge \By = I \lr{ \Bx \cross \By }\)) twice
\begin{equation}\label{eqn:lineAndPlane:100}
\begin{aligned}
\Bd \wedge \Bu \inv{\Bu}
&=
\gpgradeone{
\Bd \wedge \Bu \frac{\Bu}{\Bu^2}
} \\
&=
\inv{\Bu^2}
\gpgradeone{
I (\Bd \cross \Bu) \Bu
} \\
&=
\inv{\Bu^2}
\gpgradeone{
I (\Bd \cross \Bu) \cdot \Bu
+
I (\Bd \cross \Bu) \wedge \Bu
} \\
&=
\inv{\Bu^2}
\gpgradeone{
I^2 (\Bd \cross \Bu) \cross \Bu
} \\
&=
\frac{\Bu \cross (\Bd \cross \Bu)}{\Bu^2}.
\end{aligned}
\end{equation}
Distance from a plane.
Given two linearly independent vectors \( \Ba, \Bb \) that span a plane, and a point \( \Bx \) in the plane, the points in that plane are parameterized by
\begin{equation}\label{eqn:lineAndPlane:140}
\By(s,t) = \Bx + s \Ba + t \Bb.
\end{equation}
We can form a trivector equation of a plane by wedging both sides, first with \( \Ba \) and then with \( \Bb \), yielding
\begin{equation}\label{eqn:lineAndPlane:160}
\lr{ \Bx – \By } \wedge \Ba \wedge \Bb = 0.
\end{equation}
This equation is satisfied by all points \( \Bx, \By \) that lie in the plane
We are used to seeing the equation of a plane in dot product form, utilizing a normal. That \(\mathbb{R}^3\) representation can be recovered utilizing a dual transformation. We introduce a bivector (2-blade) representation of the plane itself
\begin{equation}\label{eqn:lineAndPlane:180}
B = \Ba \wedge \Bb,
\end{equation}
and then let
\begin{equation}\label{eqn:lineAndPlane:200}
B = I \Bn.
\end{equation}
With such a substitution, \ref{eqn:lineAndPlane:160} can be transformed
\begin{equation}\label{eqn:lineAndPlane:220}
\begin{aligned}
0
&= \lr{ \Bx – \By } \wedge B \\
&= \gpgradethree{
\lr{ \Bx – \By } B
} \\
&= \gpgradethree{
\lr{ \Bx – \By } I \Bn
} \\
&= \gpgradethree{
I \lr{ \Bx – \By } \cdot \Bn
+
I \lr{ \Bx – \By } \wedge \Bn
} \\
&=
I \lr{ \Bx – \By } \cdot \Bn,
\end{aligned}
\end{equation}
where the last wedge product could be discarded since it contributes only a vector grade object after multiplication with \( I \), and that is filtered out by the grade three selection. Multiplication of both sides with \( -I \) yields
\begin{equation}\label{eqn:lineAndPlane:240}
\lr{ \Bx – \By } \cdot \Bn = 0,
\end{equation}
the conventional form of the equation of an \(\mathbb{R}^3\) plane.
If we want a more general representation, then we are better off using the wedge product form of this equation
\begin{equation}\label{eqn:lineAndPlane:280}
\lr{ \Bx – \By } \wedge B = 0,
\end{equation}
where we use \ref{eqn:lineAndPlane:180} to drop the references to the original spanning vectors \( \Ba, \Bb \). As with rotations, in geometric algebra, it is more natural to encode the orientation of the plane with a bivector, than to use a spanning pair of vectors in the plane, or the normal to the plane.
For the question of shortest distance from a point to our plane, we want to compute the component of \( \Bd = \Bx – \Bs \) that lies in the plane represented by \( B \), and the component perpendicular to that plane. We do so using the same method as above for the line distance problem, writing
\begin{equation}\label{eqn:lineAndPlane:300}
\begin{aligned}
\Bd
&= \Bd B \inv{B} \\
&=
\lr{ \Bd \cdot B } \inv{B}
+
\lr{ \Bd \wedge B } \inv{B}.
\end{aligned}
\end{equation}
It turns out that these are both vector grade objects (i.e. there are no non-vector grades that cancel perfectly). The first term is the projection of \( \Bd \) onto the plane \( B \) whereas the second term is the rejection. Let’s do a few things here to get comfortable with these components. First, let’s verify that they are perpendicular by computing their dot product
\begin{equation}\label{eqn:lineAndPlane:320}
\begin{aligned}
\lr{ \lr{ \Bd \cdot B } \inv{B} }
\cdot
\lr{ \lr{ \Bd \wedge B } \inv{B} }
&=
\gpgradezero{
\lr{ \Bd \cdot B } \inv{B}
\lr{ \Bd \wedge B } \inv{B}
} \\
&=
\inv{B^4}
\gpgradezero{
\lr{ \Bd \cdot B } B
\lr{ \Bd \wedge B } B
} \\
&\propto
\gpgradezero{
\lr{ \Bd \cdot B } B^2
\lr{ \Bd \wedge B }
} \\
&\propto
\gpgradezero{
\lr{ \Bd \cdot B }
\lr{ \Bd \wedge B }
} \\
&=
0,
\end{aligned}
\end{equation}
where we first used \( B^{-1} = B/B^2 \), then \( \lr{ \Bd \wedge B } B = \pm B \lr{ \Bd \wedge B } \) (for \(\mathbb{R}^3\) \( B \) commutes with the wedge \( \Bd \wedge B \) is a pseudoscalar, but may anticommute in other dimensions). Finally, within the scalar selection operator we are left with the products of grade-1 and grade-3 objects, which can have only grade 2 or grade 4 components, so the scalar selection is zero.
To confirm the guess that \( \lr{ \Bd \cdot B } \inv{B} \) lies in the plane, we can expand this object in terms of the spanning vector pair \( \Ba, \Bb \) to find
\begin{equation}\label{eqn:lineAndPlane:340}
\begin{aligned}
\lr{ \Bd \cdot B } \inv{B}
&=
\lr{ \Bd \cdot \lr{ \Ba \wedge \Bb} } \inv{B} \\
&=
\lr{
(\Bd \cdot \Ba) \Bb
–
(\Bd \cdot \Bb) \Ba
} \inv{B} \\
&\propto
\lr{
u \Ba + v \Bb
}
\cdot \lr{ \Ba \wedge \Bb} \\
&\in \setlr{ \Ba, \Bb }
\end{aligned}
\end{equation}
Similarly, if \( \lr{ \Bd \cdot B } \inv{B} \) has any component in the plane, dotting with \( B \) should be non-zero, but we have
\begin{equation}\label{eqn:lineAndPlane:360}
\begin{aligned}
\lr{ \lr{ \Bd \cdot B } \inv{B} } \cdot B
&=
\gpgradeone{ \lr{ \Bd \cdot B } \inv{B} B } \\
&=
\gpgradeone{ \Bd \cdot B } \\
&= 0,
\end{aligned}
\end{equation}
which demonstrates that this is the component we are interested in. The directed (shortest) distance from the point \( \Bs \) to the plane is therefore
\begin{equation}\label{eqn:lineAndPlane:380}
\BD
=
\lr{ \lr{ \Bx – \Bs } \wedge B } \inv{B}.
\end{equation}
There should be a dual form for this relationship too, so let’s see what it looks like. First note that for vector \( \Bd \)
\begin{equation}\label{eqn:lineAndPlane:400}
\begin{aligned}
\Bd \wedge B
&=
\gpgradethree{
\Bd I \Bn
} \\
&=
I (\Bd \cdot \Bn),
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:lineAndPlane:420}
\begin{aligned}
\BD
&=
I \lr{ \lr{ \Bx – \Bs } \cdot \Bn } \inv{I \Bn} \\
&=
\lr{ \Bx – \Bs } \cdot \Bn \inv{\Bn}.
\end{aligned}
\end{equation}
This would conventionally be written in terms of a unit vector \( \ncap \) as \( \lr{\lr{ \Bx – \Bs } \cdot \ncap} \ncap\).
Summary.
We can write the equation of a line, plane, (volume, …) in a uniform fashion as
\begin{equation}\label{eqn:lineAndPlane:440}
\lr{ \By – \Bx } \wedge V = 0,
\end{equation}
where \( V = \Bu_1, \Bu_1 \wedge \Bu_2, \Bu_1 \wedge \Bu_2 \wedge \cdots \wedge \Bu_n \) depending on the dimenion of the desired subspace, where \( \Bu_k \) are linearly independent vectors spanning that space, and \( \Bx \) is one point in that subspace.
The (directed) distance from a vector \( \Bs \) to that subspace is given by
\begin{equation}\label{eqn:lineAndPlane:460}
\BD = \lr{ \Bx – \Bs } \wedge V \inv{V}.
\end{equation}
For the \(\mathbb{R}^3\) special case of a line, where \( V = \ucap \) is a unit vector on the line, we showed that this reduces to
\begin{equation}\label{eqn:lineAndPlane:480}
\BD = \ucap \cross \lr{ \lr{ \Bx – \Bs } \cross \ucap },
\end{equation}
For the \(\mathbb{R}^3\) special case of a line, where \( V = I \ncap \) is a unit bivector representing the plane, we found that we could write \ref{eqn:lineAndPlane:460} as a projection onto the normal to the plane
\begin{equation}\label{eqn:lineAndPlane:500}
\BD = \lr{ \lr{ \Bx – \Bs } \cdot \ncap } \ncap.
\end{equation}
Again, only for \(\mathbb{R}^3\) we were also able to write the equation of the plane itself in dual form as
\begin{equation}\label{eqn:lineAndPlane:520}
\lr{ \By – \Bx } \cdot \ncap = 0.
\end{equation}
These dual forms would also be possible for other special cases (like the equation of a volume in \(\mathbb{R}^4\) and the distance from a point to that volume), but should we desire general relationships valid in all dimension (even \(\mathbb{R}^2\)), we can stick to \ref{eqn:lineAndPlane:440} and \ref{eqn:lineAndPlane:460}.
References
[1] David Vernon Widder. Advanced calculus. Courier Corporation, 1989.
Like this:
Like Loading...





















