[Click here for a PDF of this post with nicer formatting]
Motivation
In class, an overview of the Fresnel relations for a TE mode electric field were presented. Here’s a fleshing out of the details is presented, as well as the equivalent for the TM mode.
Single interface TE mode.
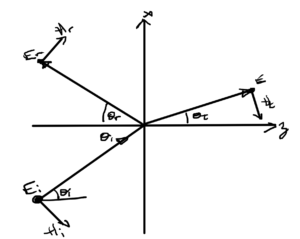
The Fresnel reflection geometry for an electric field \( \BE \) parallel to the interface (TE mode) is sketched in fig. 1.
\begin{equation}\label{eqn:emtLecture10:20}
\boldsymbol{\mathcal{E}}_i = \Be_2 E_i e^{j \omega t – j \Bk_{i} \cdot \Bx },
\end{equation}
with an assumption that this field maintains it’s polarization in both its reflected and transmitted components, so that
\begin{equation}\label{eqn:emtLecture10:40}
\boldsymbol{\mathcal{E}}_r = \Be_2 r E_i e^{j \omega t – j \Bk_{r} \cdot \Bx },
\end{equation}
and
\begin{equation}\label{eqn:emtLecture10:60}
\boldsymbol{\mathcal{E}}_t = \Be_2 t E_i e^{j \omega t – j \Bk_{t} \cdot \Bx },
\end{equation}
Measuring the angles \( \theta_i, \theta_r, \theta_t \) from the normal, with \( i = \Be_3 \Be_1 \) the wave vectors are
\begin{equation}\label{eqn:emtLecture10:620}
\begin{aligned}
\Bk_{i} &= \Be_3 k_1 e^{i\theta_i} = k_1\lr{ \Be_3 \cos\theta_i + \Be_1\sin\theta_i } \\
\Bk_{r} &= -\Be_3 k_1 e^{-i\theta_r} = k_1 \lr{ -\Be_3 \cos\theta_r + \Be_1 \sin\theta_r } \\
\Bk_{t} &= \Be_3 k_2 e^{i\theta_t} = k_2 \lr{ \Be_3 \cos\theta_t + \Be_1 \sin\theta_t }
\end{aligned}
\end{equation}
So the time harmonic electric fields are
\begin{equation}\label{eqn:emtLecture10:640}
\begin{aligned}
\BE_i &= \Be_2 E_i \exp\lr{ – j k_1 \lr{ z\cos\theta_i + x \sin\theta_i} } \\
\BE_r &= \Be_2 r E_i \exp\lr{ – j k_1 \lr{ -z \cos\theta_r + x \sin\theta_r}} \\
\BE_t &= \Be_2 t E_i \exp\lr{ – j k_2 \lr{ z \cos\theta_t + x \sin\theta_t}}.
\end{aligned}
\end{equation}
The magnetic fields follow from Faraday’s law
\begin{equation}\label{eqn:emtLecture10:900}
\begin{aligned}
\BH
&= \inv{-j \omega \mu } \spacegrad \cross \BE \\
&= \inv{-j \omega \mu } \spacegrad \cross \Be_2 e^{-j \Bk \cdot \Bx} \\
&= \inv{j \omega \mu } \Be_2 \cross \spacegrad e^{-j \Bk \cdot \Bx} \\
&= -\inv{\omega \mu } \Be_2 \cross \Bk e^{-j \Bk \cdot \Bx} \\
&= \inv{\omega \mu } \Bk \cross \BE
\end{aligned}
\end{equation}
We have
\begin{equation}\label{eqn:emtLecture10:920}
\begin{aligned}
\kcap_{i} \cross \Be_2 &= -\Be_1 \cos\theta_i + \Be_3\sin\theta_i \\
\kcap_{r} \cross \Be_2 &= \Be_1 \cos\theta_r + \Be_3 \sin\theta_r \\
\kcap_{t} \cross \Be_2 &= -\Be_1 \cos\theta_t + \Be_3 \sin\theta_t,
\end{aligned}
\end{equation}
Note that
\begin{equation}\label{eqn:emtLecture10:1500}
\begin{aligned}
\frac{k}{\omega \mu}
&=
\frac{k}{k v \mu} \\
&=
\frac{\sqrt{\mu\epsilon}}{\mu} \\
&=\sqrt
{
\frac{\epsilon}{\mu}
} \\
&=
\inv{\eta}.
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:emtLecture10:940}
\begin{aligned}
\BH_{i} &= \frac{ E_i}{\eta_1} \lr{ -\Be_1 \cos\theta_i + \Be_3\sin\theta_i } \exp\lr{ – j k_1 \lr{ z\cos\theta_i + x \sin\theta_i} } \\
\BH_{r} &= \frac{ r E_i}{\eta_1} \lr{ \Be_1 \cos\theta_r + \Be_3 \sin\theta_r } \exp\lr{ – j k_1 \lr{ -z \cos\theta_r + x \sin\theta_r}} \\
\BH_{t} &= \frac{ t E_i}{\eta_2} \lr{ -\Be_1 \cos\theta_t + \Be_3 \sin\theta_t } \exp\lr{ – j k_2 \lr{ z \cos\theta_t + x \sin\theta_t}}.
\end{aligned}
\end{equation}
The boundary conditions at \( z = 0 \) with \( \ncap = \Be_3 \) are
\begin{equation}\label{eqn:emtLecture10:960}
\begin{aligned}
\ncap \cross \BH_1 &= \ncap \cross \BH_2 \\
\ncap \cdot \BB_1 &= \ncap \cdot \BB_2 \\
\ncap \cross \BE_1 &= \ncap \cross \BE_2 \\
\ncap \cdot \BD_1 &= \ncap \cdot \BD_2,
\end{aligned}
\end{equation}
At \( x = 0 \), this is
\begin{equation}\label{eqn:emtLecture10:1060}
\begin{aligned}
-\frac{1}{\eta_1} \cos\theta_i + \frac{r }{\eta_1} \cos\theta_r &= -\frac{t }{\eta_2} \cos\theta_t \\
k_1 \sin\theta_i + k_1 r \sin\theta_r &= k_2 t \sin\theta_t \\
1 + r &= t
\end{aligned}
\end{equation}
When \( t = 0 \) the latter two equations give Shell’s first law
\begin{equation}\label{eqn:emtLecture10:1080}
\boxed{
\sin\theta_i = \sin\theta_r.
}
\end{equation}
Assuming this holds for all \( r, t \) we have
\begin{equation}\label{eqn:emtLecture10:1120}
k_1 \sin\theta_i (1 + r ) = k_2 t \sin\theta_t,
\end{equation}
which is Snell’s second law in disguise
\begin{equation}\label{eqn:emtLecture10:1140}
k_1 \sin\theta_i = k_2 \sin\theta_t.
\end{equation}
With
\begin{equation}\label{eqn:emtLecture10:1540}
\begin{aligned}
k
&= \frac{\omega}{v} \\
&= \frac{\omega}{c} \frac{c}{v} \\
&= \frac{\omega}{c} n,
\end{aligned}
\end{equation}
so \ref{eqn:emtLecture10:1140} takes the form
\begin{equation}\label{eqn:emtLecture10:1560}
\boxed{
n_1 \sin\theta_i = n_2 \sin\theta_t.
}
\end{equation}
With
\begin{equation}\label{eqn:emtLecture10:1200}
\begin{aligned}
k_{1z} &= k_1 \cos\theta_i \\
k_{2z} &= k_2 \cos\theta_t,
\end{aligned}
\end{equation}
we can solve for \( r, t \) by inverting
\begin{equation}\label{eqn:emtLecture10:1180}
\begin{bmatrix}
\mu_2 k_{1z} & \mu_1 k_{2z} \\
-1 & 1 \\
\end{bmatrix}
\begin{bmatrix}
r \\
t
\end{bmatrix}
=
\begin{bmatrix}
\mu_2 k_{1z} \\
1
\end{bmatrix},
\end{equation}
which gives
\begin{equation}\label{eqn:emtLecture10:1220}
\begin{bmatrix}
r \\
t
\end{bmatrix}
=
\begin{bmatrix}
1 & -\mu_1 k_{2z} \\
1 & \mu_2 k_{1z}
\end{bmatrix}
\begin{bmatrix}
\mu_2 k_{1z} \\
1
\end{bmatrix},
\end{equation}
or
\begin{equation}\label{eqn:emtLecture10:1240}
\boxed{
\begin{aligned}
r &= \frac{\mu_2 k_{1z} – \mu_1 k_{2z}}{\mu_2 k_{1z} + \mu_1 k_{2z}} \\
t &= \frac{2 \mu_2 k_{1z}}{\mu_2 k_{1z} + \mu_1 k_{2z}}
\end{aligned}
}
\end{equation}
There are many ways that this can be written. Dividing both the numerator and denominator by \( \mu_1 \mu_2 \omega/c \), and noting that \( k = \omega n/c \), we have
\begin{equation}\label{eqn:emtLecture10:1680}
\begin{aligned}
r &= \frac
{ \frac{n_1}{\mu_1} \cos\theta_i – \frac{n_2}{\mu_2} \cos\theta_t }
{ \frac{n_1}{\mu_1} \cos\theta_i + \frac{n_2}{\mu_2} \cos\theta_t } \\
t &=
\frac{ 2 \frac{n_1}{\mu_1} \cos\theta_i }
{ \frac{n_1}{\mu_1} \cos\theta_i + \frac{n_2}{\mu_2} \cos\theta_t },
\end{aligned}
\end{equation}
which checks against (4.32,4.33) in [1].
Single interface TM mode.
For completeness, now consider the TM mode.
Faraday’s law also can provide the electric field from the magnetic
\begin{equation}\label{eqn:emtLecture10:1280}
\begin{aligned}
\kcap \cross \BH
&= \eta \kcap \cross \lr{ \kcap \cross \BE } \\
&= -\eta \kcap \cdot \lr{ \kcap \wedge \BE } \\
&= -\eta \lr{ \BE – \kcap \lr{ \kcap \cdot \BE } } \\
&= -\eta \BE.
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:emtLecture10:1300}
\BE = \eta \BH \cross \kcap.
\end{equation}
So the magnetic and electric fields are
\label{eqn:emtLecture10:1520}
\begin{equation}\label{eqn:emtLecture10:1320}
\begin{aligned}
\BH_i &= \Be_2 \frac{E_i}{\eta_1} \exp\lr{ – j k_1 \lr{ z\cos\theta_i + x \sin\theta_i} } \\
\BH_r &= \Be_2 r \frac{E_i}{\eta_1} \exp\lr{ – j k_1 \lr{ -z \cos\theta_r + x \sin\theta_r}} \\
\BH_t &= \Be_2 t \frac{E_i}{\eta_2} \exp\lr{ – j k_2 \lr{ z \cos\theta_t + x \sin\theta_t}}
\end{aligned}
\end{equation}
\begin{equation}\label{eqn:emtLecture10:1340}
\begin{aligned}
\BE_{i} &= -E_i \lr{ -\Be_1 \cos\theta_i + \Be_3\sin\theta_i } \exp\lr{ – j k_1 \lr{ z\cos\theta_i + x \sin\theta_i} } \\
\BE_{r} &= -r E_i \lr{ \Be_1 \cos\theta_r + \Be_3 \sin\theta_r } \exp\lr{ – j k_1 \lr{ -z \cos\theta_r + x \sin\theta_r}} \\
\BE_{t} &= -t E_i \lr{ -\Be_1 \cos\theta_t + \Be_3 \sin\theta_t } \exp\lr{ – j k_2 \lr{ z \cos\theta_t + x \sin\theta_t}}.
\end{aligned}
\end{equation}
Imposing the constraints \ref{eqn:emtLecture10:960}, at \( x = z = 0 \) we have
\begin{equation}\label{eqn:emtLecture10:1440}
\begin{aligned}
\inv{\eta_1}\lr{1 + r} &= \frac{t}{\eta_2} \\
\cos\theta_i – r \cos\theta_r &= t \cos\theta_t \\
\epsilon_1 \lr{ \sin\theta_i + r \sin\theta_r} &= t \epsilon_2 \sin\theta_t
\end{aligned}.
\end{equation}
At \( t = 0 \), the first and third of these give \( \theta_i = \theta_r \). Assuming this incident and reflection angle equality holds for all values of \( t \), we have
\begin{equation}\label{eqn:emtLecture10:1580}
\begin{aligned}
\sin\theta_i(1 + r) &= t \frac{\epsilon_2}{\epsilon_1} \sin\theta_t \\
\sin\theta_i \frac{\eta_1}{\eta_2} t &=
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:emtLecture10:1600}
\epsilon_1 \eta_1 \sin\theta_i = \epsilon_2 \eta_2 \sin\theta_t.
\end{equation}
This is also Snell’s second law \ref{eqn:emtLecture10:1560} in disguise, which can be seen by
\begin{equation}\label{eqn:emtLecture10:1620}
\begin{aligned}
\epsilon_1 \eta_1
&=
\epsilon_1 \sqrt{\frac{\mu_1}{\epsilon_1}} \\
&=
\sqrt{\epsilon_1 \mu_1} \\
&=
\inv{v} \\
&=
\frac{n}{c}.
\end{aligned}
\end{equation}
The remaining equations in matrix form are
\begin{equation}\label{eqn:emtLecture10:1460}
\begin{bmatrix}
\cos\theta_i & \cos\theta_t \\
-1 & \frac{\eta_1}{\eta_2}
\end{bmatrix}
\begin{bmatrix}
r \\
t
\end{bmatrix}
=
\begin{bmatrix}
\cos\theta_i \\
1
\end{bmatrix},
\end{equation}
the inverse of which is
\begin{equation}\label{eqn:emtLecture10:1480}
\begin{bmatrix}
r \\
t
\end{bmatrix}
=
\inv{ \frac{\eta_1}{\eta_2} \cos\theta_i + \cos\theta_t }
\begin{bmatrix}
\frac{\eta_1}{\eta_2} & – \cos\theta_t \\
1 & \cos\theta_i
\end{bmatrix}
\begin{bmatrix}
\cos\theta_i \\
1
\end{bmatrix}
=
\inv{ \frac{\eta_1}{\eta_2} \cos\theta_i + \cos\theta_t }
\begin{bmatrix}
\frac{\eta_1}{\eta_2} \cos\theta_i – \cos\theta_t \\
2 \cos\theta_i
\end{bmatrix},
\end{equation}
or
\begin{equation}\label{eqn:emtLecture10:1640}
\boxed{
\begin{aligned}
r
&=
\frac{\eta_1 \cos\theta_i – \eta_2 \cos\theta_t }{ \eta_1 \cos\theta_i + \eta_2 \cos\theta_t } \\
t &=
\frac{2 \eta_2 \cos\theta_i}{ \eta_1 \cos\theta_i + \eta_2 \cos\theta_t }.
\end{aligned}
}
\end{equation}
Multiplication of the numerator and denominator by \( c/\eta_1 \eta_2 \), noting that \( c/\eta = n/\mu \) gives
\begin{equation}\label{eqn:emtLecture10:1700}
\begin{aligned}
r
&=
\frac{\frac{n_2}{\mu_2} \cos\theta_i – \frac{n_1}{\mu_1} \cos\theta_t }{ \frac{n_2}{\mu_2} \cos\theta_i + \frac{n_1}{\mu_1} \cos\theta_t } \\
t &=
\frac{2 \frac{n_1}{\mu_1} \cos\theta_i }{ \frac{n_2}{\mu_2} \cos\theta_i + \frac{n_1}{\mu_1} \cos\theta_t } \\
\end{aligned}
\end{equation}
which checks against (4.38,4.39) in [1].
References
[1] E. Hecht. Optics. 1998.