[Click here for a PDF of this post with nicer formatting]
DISCLAIMER: Very rough notes from class (today VERY VERY rough).
These are notes for the UofT course PHY2403H, Quantum Field Theory, taught by Prof. Erich Poppitz, fall 2018.
Review: S-matrix
We defined an \( S-\)matrix
\begin{equation}\label{eqn:qftLecture17:20}
\bra{f} S \ket{i} = S_{fi} = \lr{ 2 \pi }^4 \delta^{(4)} \lr{ \sum \lr{p_i – \sum_{p_f} } } i M_{fi},
\end{equation}
where
\begin{equation}\label{eqn:qftLecture17:40}
i M_{fi} = \sum \text{ all connected amputated Feynman diagrams }.
\end{equation}
The matrix element \( \bra{f} S \ket{i} \) is the amplitude of the transition from the initial to the final state. In general this can get very complicated, as the number of terms grows factorially with the order.
We also talked about decays.
Scattering in a scalar theory
Suppose that we have a scalar theory with a light field \( \Phi, M \) and a heavy field \( \varphi, m \), where \( m > 2 M \). Perhaps we have an interaction with a \( z^2 \) symmetry so that the interaction potential is quadratic in \( \Phi \)
\begin{equation}\label{eqn:qftLecture17:60}
V_{\text{int}} = \mu \varphi \Phi \Phi.
\end{equation}
We may have \( \Phi \Phi \rightarrow \Phi \Phi \) scattering.
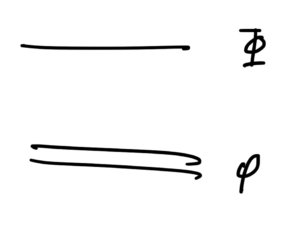
We will denote diagrams using a double line for \( \phi \) and a single line for \( \Phi \), as sketched in
fig. 1. Particle line convention.
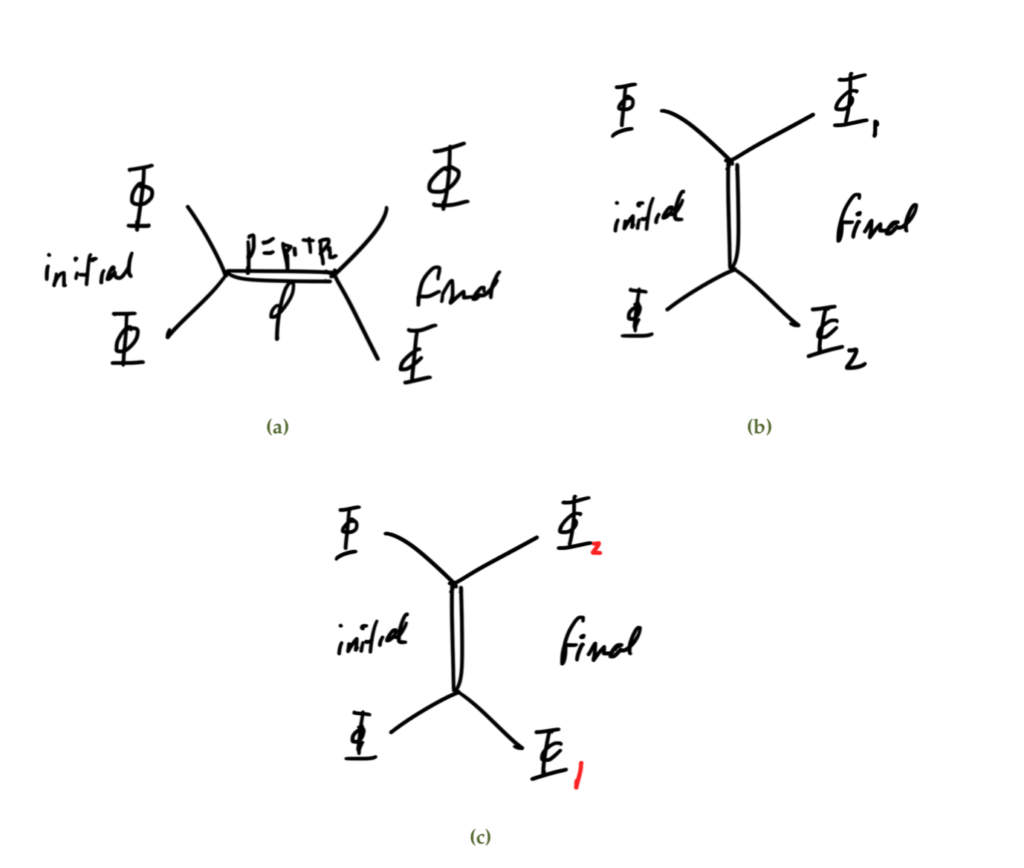
There are three possible diagrams:
fig 2. Possible diagrams.
The first we will call the s-channel, which has amplitude
\begin{equation}\label{eqn:qftLecture17:80}
A(\text{s-channel}) \sim \frac{i}{p^2 – m^2 + i \epsilon} =
\frac{i}{s – m^2 + i \epsilon}
\end{equation}
\begin{equation}\label{eqn:qftLecture17:100}
(p_1 + p_2)^2 = s
\end{equation}
In the centre of mass frame
\begin{equation}\label{eqn:qftLecture17:120}
\Bp_1 = – \Bp_2,
\end{equation}
so
\begin{equation}\label{eqn:qftLecture17:140}
s = \lr{ p_1^0 + p_2^0 }^2 = E_{\text{cm}}^2.
\end{equation}
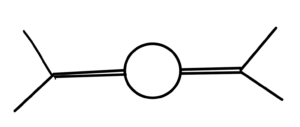
To the next order we have a diagram like fig. 3.
fig. 3. Higher order.
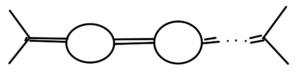
and can have additional virtual particles created, with diagrams like fig. 4.
fig. 4. More virtual particles.
We will see (QFT II) that this leads to an addition imaginary \( i \Gamma \) term in the propagator
\begin{equation}\label{eqn:qftLecture17:160}
\frac{i}{s – m^2 + i \epsilon}
\rightarrow
\frac{i}{s – m^2 – i m \Gamma + i \epsilon}.
\end{equation}
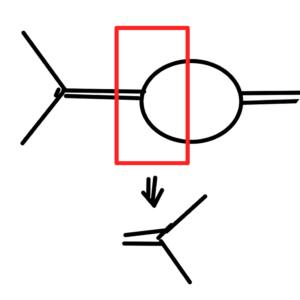
If we choose to zoom into the such a figure, as sketched in fig. 5, we find that it contains the interaction of interest for our diagram, so we can (looking forward to currently unknown material) know that our diagram also has such an imaginary \( i \Gamma \) term in its propagator.
fig. 5. Zooming into the diagram for a higher order virtual particle creation event.
Assuming such a term, the squared amplitude becomes
\begin{equation}\label{eqn:qftLecture17:180}
\evalbar{\sigma}{s \text{near} m^2}
\sim
\Abs{A_s}^2 \sim \inv{(s – m)^2 + m^2 \Gamma^2}
\end{equation}
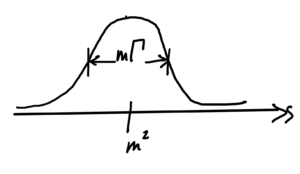
This is called a resonance (name?), and is sketched in fig. 6.
fig. 6. Resonance.
Where are the poles of the modified propagator?
\begin{equation}\label{eqn:qftLecture17:220}
\frac{i}{s – m^2 – i m \Gamma + i \epsilon}
=
\frac{i}{p_0^2 – \Bp^2 – m^2 – i m \Gamma + i \epsilon}
\end{equation}
The pole is found, neglecting \( i \epsilon \), is found at
\begin{equation}\label{eqn:qftLecture17:200}
\begin{aligned}
p_0
&= \sqrt{ \omega_\Bp^2 + i m \Gamma } \\
&= \omega_\Bp \sqrt{ 1 + \frac{i m \Gamma }{\omega_\Bp^2} } \\
&\approx \omega_\Bp + \frac{i m \Gamma }{2 \omega_\Bp}
\end{aligned}
\end{equation}
Decay rates.
We have an initial state
\begin{equation}\label{eqn:qftLecture17:240}
\ket{i} = \ket{k},
\end{equation}
and final state
\begin{equation}\label{eqn:qftLecture17:260}
\ket{f} = \ket{p_1^f, p_2^f \cdots p_n^f}.
\end{equation}
We defined decay rate as the ratio of the number of initial particles to the number of final particles.
The probability is
\begin{equation}\label{eqn:qftLecture17:280}
\rho \sim \Abs{\bra{f} S \ket{i}}^2
=
(2 \pi)^4 \delta^{(4)}( p_{\text{in}} – \sum p_f )
(2 \pi)^4 \delta^{(4)}( p_{\text{in}} – \sum p_f )
\times \Abs{ M_{fi} }^2
\end{equation}
Saying that \( \delta(x) f(x) = \delta(x) f(0) \) we can set the argument of one of the delta functions to zero, which gives us a vacuum volume element factor
\begin{equation}\label{eqn:qftLecture17:300}
(2 \pi)^4
\delta^{(4)}( p_{\text{in}} – \sum p_f ) =
(2 \pi)^4
\delta^{(4)}( 0 )
= V_3 T,
\end{equation}
so
\begin{equation}\label{eqn:qftLecture17:320}
\frac{\text{probability for \( i \rightarrow f\)}}{\text{unit time}}
\sim
(2 \pi)^4 \delta^{(4)}( p_{\text{in}} – \sum p_f )
V_3
\times \Abs{ M_{fi} }^2
\end{equation}
\begin{equation}\label{eqn:qftLecture17:340}
\braket{\Bk}{\Bk} = 2 \omega_\Bk V_3
\end{equation}
coming from
\begin{equation}\label{eqn:qftLecture17:360}
\braket{k}{p} = (2 \pi)^3 2 \omega_\Bp \delta^{(3)}(\Bp – \Bk)
\end{equation}
so
\begin{equation}\label{eqn:qftLecture17:380}
\braket{k}{k} = 2 \omega_\Bp V_3
\end{equation}
\begin{equation}\label{eqn:qftLecture17:400}
\frac{\text{probability for \(i \rightarrow f\)}}{\text{unit time}}
\sim
\frac{
(2 \pi)^4 \delta^{(4)}( p_{\text{in}} – \sum p_f )
\Abs{ M_{fi} }^2 V_3
}
{
2 \omega_\Bk V_3
2 \omega_{\Bp_1}
\cdots
2 \omega_{\Bp_n} V_3^n
}
\end{equation}
If we multiply the number of final states with \( p_i^f \in (p_i^f, p_i^f + dp_i^f) \) for a particle in a box
\begin{equation}\label{eqn:qftLecture17:420}
p_x = \frac{ 2 \pi n_x}{L}
\end{equation}
\begin{equation}\label{eqn:qftLecture17:440}
\Delta p_x = \frac{ 2 \pi }{L} \Delta n_x
\end{equation}
\begin{equation}\label{eqn:qftLecture17:460}
\Delta n_x
=
\frac{L}{2 \pi} \Delta p_x
\end{equation}
and
\begin{equation}\label{eqn:qftLecture17:480}
\Delta n_x
\Delta n_y
\Delta n_z
= \frac{V_3}{(2 \pi)^3 }
\Delta p_x
\Delta p_y
\Delta p_z
\end{equation}
\begin{equation}\label{eqn:qftLecture17:500}
\begin{aligned}
\Gamma
&=
\frac{\text{number of events \( i \rightarrow f \)}}{\text{unit time}} \\
&=
\prod_{f} \frac{ d^3 p}{(2 \pi)^3 2 \omega_{\Bp^f} }
\frac{ (2 \pi)^4 \delta^{(4)}( k – \sum_f p^f ) \Abs{M_{fi}}^2 }
{
2 \omega_{\Bk}
}
\end{aligned}
\end{equation}
Note that everything here is Lorentz invariant except for the denominator of the second term ( \(2 \omega_{\Bk}\)). This is a well known result (the decay rate changes in different frames).
Cross section.
For \( 2 \rightarrow \text{many} \) transitions
\begin{equation}\label{eqn:qftLecture17:520}
\frac{\text{probability \( i \rightarrow f \)}}{\text{unit time}}
\times \lr{
\text{ number of final states with \( p_f \in (p_f, p_f + dp_f) \)
}
}
=
\frac{ (2 \pi)^4 \delta^{(4)}( \sum p_i – \sum_f p^f ) \Abs{M_{fi}}^2 {V_3} }
{
2 \omega_{\Bk_1} V_3
2 \omega_{\Bk_2} {V_3 }
}
\prod_{f} \frac{ d^3 p}{(2 \pi)^3 2 \omega_{\Bp^f} }
\end{equation}
We need to divide by the flux.
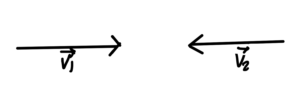
In the CM frame, as sketched in fig. 7, the current is
\begin{equation}\label{eqn:qftLecture17:540}
\Bj = n \Bv_1 – n \Bv_2,
\end{equation}
so if the density is
\begin{equation}\label{eqn:qftLecture17:560}
n = \inv{V_3},
\end{equation}
(one particle in \(V_3\)), then
\begin{equation}\label{eqn:qftLecture17:580}
\Bj = \frac{\Bv_1 – \Bv_2}{V_3}.
\end{equation}
fig. 7. Centre of mass frame.
This is where [1] stops,
\begin{equation}\label{eqn:qftLecture17:640}
\sigma
=
\frac{ (2 \pi)^4 \delta^{(4)}( \sum p_i – \sum_f p^f ) \Abs{M_{fi}}^2 {V_3} }
{
2 \omega_{\Bk_1}
2 \omega_{\Bk_2}
\Abs{\Bv_1 – \Bv_2}
}
\prod_{f} \frac{ d^3 p}{(2 \pi)^3 2 \omega_{\Bp^f} }
\end{equation}
There is, however, a nice Lorentz invariant generalization
\begin{equation}\label{eqn:qftLecture17:600}
j = \inv{ V_3 \omega_{k_A} \omega_{k_B}} \sqrt{ (k_A – k_B)^2 – m_A^2 m_B^2 }
\end{equation}
(Claim: DIY)
\begin{equation}\label{eqn:qftLecture17:620}
\begin{aligned}
\evalbar{j}{CM}
&=
\inv{V_3}
\lr{
\frac{\Abs{\Bk}}{\omega_{k_A}}
+
\frac{\Abs{\Bk}}{\omega_{k_B}}
} \\
&=
\inv{V_3} \lr{ \Abs{\Bv_A} + \Abs{\Bv_B} } \\
&=
\inv{V_3} \Abs{\Bv_1 – \Bv_2 }.
\end{aligned}
\end{equation}
\begin{equation}\label{eqn:qftLecture17:660}
\sigma
=
\frac{ (2 \pi)^4 \delta^{(4)}( \sum p_i – \sum_f p^f ) \Abs{M_{fi}}^2 {V_3} }
{
4 \sqrt{ (k_A – k_B)^2 – m_A^2 m_B^2 }
}
\prod_{f} \frac{ d^3 p}{(2 \pi)^3 2 \omega_{\Bp^f} }.
\end{equation}
References
[1] Michael E Peskin and Daniel V Schroeder. An introduction to Quantum Field Theory. Westview, 1995.