[Click here for a PDF of this post with nicer formatting]
DISCLAIMER: Very rough notes from class, with some additional side notes.
These are notes for the UofT course PHY2403H, Quantum Field Theory, taught by Prof. Erich Poppitz, fall 2018.
Review
Given a field \( \phi(t_0, \Bx) \), satisfying the commutation relations
\begin{equation}\label{eqn:qftLecture14:20}
\antisymmetric{\pi(t_0, \Bx)}{\phi(t_0, \By)} = -i \delta(\Bx – \By)
\end{equation}
we introduced an interaction picture field given by
\begin{equation}\label{eqn:qftLecture14:40}
\phi_I(t, x) = e^{i H_0(t- t_0)} \phi(t_0, \Bx) e^{-iH_0(t – t_0)}
\end{equation}
related to the Heisenberg picture representation by
\begin{equation}\label{eqn:qftLecture14:60}
\phi_H(t, x)
= e^{i H(t- t_0)} \phi(t_0, \Bx) e^{-iH(t – t_0)}
= U^\dagger(t, t_0) \phi_I(t, \Bx) U(t, t_0),
\end{equation}
where \( U(t, t_0) \) is the time evolution operator.
\begin{equation}\label{eqn:qftLecture14:80}
U(t, t_0) =
e^{i H_0(t – t_0)}
e^{-i H(t – t_0)}
\end{equation}
We argued that
\begin{equation}\label{eqn:qftLecture14:100}
i \PD{t}{} U(t, t_0) = H_{\text{I,int}}(t) U(t, t_0)
\end{equation}
We found the glorious expression
\begin{equation}\label{eqn:qftLecture14:120}
\boxed{
\begin{aligned}
U(t, t_0)
&= T \exp{\lr{ -i \int_{t_0}^t H_{\text{I,int}}(t’) dt’}} \\
&=
\sum_{n = 0}^\infty \frac{(-i)^n}{n!} \int_{t_0}^t dt_1 dt_2 \cdots dt_n T\lr{ H_{\text{I,int}}(t_1) H_{\text{I,int}}(t_2) \cdots H_{\text{I,int}}(t_n) }
\end{aligned}
}
\end{equation}
However, what we are really after is
\begin{equation}\label{eqn:qftLecture14:140}
\bra{\Omega} T(\phi(x_1) \cdots \phi(x_n)) \ket{\Omega}
\end{equation}
Such a product has many labels and names, and we’ll describe it as “vacuum expectation values of time-ordered products of arbitrary #’s of local Heisenberg operators”.
Perturbation
Following section 4.2, [1].
\begin{equation}\label{eqn:qftLecture14:160}
\begin{aligned}
H &= \text{exact Hamiltonian} = H_0 + H_{\text{int}}
\\
H_0 &= \text{free Hamiltonian.
}
\end{aligned}
\end{equation}
We know all about \( H_0 \) and assume that it has a lowest (ground state) \( \ket{0} \), the “vacuum” state of \( H_0 \).
\( H \) has eigenstates, in particular \( H \) is assumed to have a unique ground state \( \ket{\Omega} \) satisfying
\begin{equation}\label{eqn:qftLecture14:180}
H \ket{\Omega} = \ket{\Omega} E_0,
\end{equation}
and has states \( \ket{n} \), representing excited (non-vacuum states with energies > \( E_0 \)).
These states are assumed to be a complete basis
\begin{equation}\label{eqn:qftLecture14:200}
\mathbf{1} = \ket{\Omega}\bra{\Omega} + \sum_n \ket{n}\bra{n} + \int dn \ket{n}\bra{n}.
\end{equation}
The latter terms may be written with a superimposed sum-integral notation as
\begin{equation}\label{eqn:qftLecture14:440}
\sum_n + \int dn
=
{\int\kern-1em\sum}_n,
\end{equation}
so the identity operator takes the more compact form
\begin{equation}\label{eqn:qftLecture14:460}
\mathbf{1} = \ket{\Omega}\bra{\Omega} + {\int\kern-1em\sum}_n \ket{n}\bra{n}.
\end{equation}
For some time \( T \) we have
\begin{equation}\label{eqn:qftLecture14:220}
e^{-i H T} \ket{0} = e^{-i H T}
\lr{
\ket{\Omega}\braket{\Omega}{0} + {\int\kern-1em\sum}_n \ket{n}\braket{n}{0}
}.
\end{equation}
We now wish to argue that the \( {\int\kern-1em\sum}_n \) term can be ignored.
Argument 1:
This is something of a fast one, but one can consider a formal transformation \( T \rightarrow T(1 – i \epsilon) \), where \( \epsilon \rightarrow 0^+ \), and consider very large \( T \). This gives
\begin{equation}\label{eqn:qftLecture14:240}
\begin{aligned}
\lim_{T \rightarrow \infty, \epsilon \rightarrow 0^+}
e^{-i H T(1 – i \epsilon)} \ket{0}
&=
\lim_{T \rightarrow \infty, \epsilon \rightarrow 0^+}
e^{-i H T(1 – i \epsilon)}
\lr{
\ket{\Omega}\braket{\Omega}{0} + {\int\kern-1em\sum}_n \ket{n}\braket{n}{0}
} \\
&=
\lim_{T \rightarrow \infty, \epsilon \rightarrow 0^+}
e^{-i E_0 T – E_0 \epsilon T}
\ket{\Omega}\braket{\Omega}{0} + {\int\kern-1em\sum}_n e^{-i E_n T – \epsilon E_n T} \ket{n}\braket{n}{0} \\
&=
\lim_{T \rightarrow \infty, \epsilon \rightarrow 0^+}
e^{-i E_0 T – E_0 \epsilon T}
\lr{
\ket{\Omega}\braket{\Omega}{0} + {\int\kern-1em\sum}_n e^{-i (E_n -E_0) T – \epsilon T (E_n – E_0)} \ket{n}\braket{n}{0}
}
\end{aligned}
\end{equation}
The limits are evaluated by first taking \( T \) to infinity, then only after that take \( \epsilon \rightarrow 0^+ \). Doing this, the sum is dominated by the ground state contribution, since each excited state also has a \( e^{-\epsilon T(E_n – E_0)} \) suppression factor (in addition to the leading suppression factor).
Argument 2:
With the hand waving required for the argument above, it’s worth pointing other (less formal) ways to arrive at the same result. We can write
\begin{equation}\label{eqn:qftLecture14:260}
sectionumInt \ket{n}\bra{n} \rightarrow
\sum_k \int \frac{d^3 p}{(2 \pi)^3} \ket{\Bp, k}\bra{\Bp, k}
\end{equation}
where \( k \) is some unknown quantity that we are summing over.
If we have
\begin{equation}\label{eqn:qftLecture14:280}
H \ket{\Bp, k} = E_{\Bp, k} \ket{\Bp, k},
\end{equation}
then
\begin{equation}\label{eqn:qftLecture14:300}
e^{-i H T} sectionumInt \ket{n}\bra{n}
=
\sum_k \int \frac{d^3 p}{(2 \pi)^3} \ket{\Bp, k} e^{-i E_{\Bp, k}} \bra{\Bp, k}.
\end{equation}
If we take matrix elements
\begin{equation}\label{eqn:qftLecture14:320}
\begin{aligned}
\bra{A}
e^{-i H T} sectionumInt \ket{n}\bra{n} \ket{B}
&=
\sum_k \int \frac{d^3 p}{(2 \pi)^3} \braket{A}{\Bp, k} e^{-i E_{\Bp, k}} \braket{\Bp, k}{B} \\
&=
\sum_k \int \frac{d^3 p}{(2 \pi)^3} e^{-i E_{\Bp, k}} f(\Bp).
\end{aligned}
\end{equation}
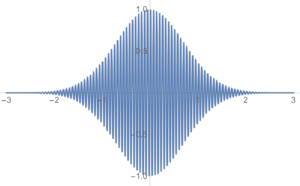
If we assume that \( f(\Bp) \) is a well behaved smooth function, we have “infinite” frequency oscillation within the envelope provided by the amplitude of that function, as depicted in fig. 1.
The Riemann-Lebesgue lemma [2] describes such integrals, the result of which is that such an integral goes to zero. This is a different sort of hand waving argument, but either way, we can argue that only the ground state contributes to the sum \ref{eqn:qftLecture14:220} above.
Ground state of the perturbed Hamiltonian.
With the excited states ignored, we are left with
\begin{equation}\label{eqn:qftLecture14:340}
e^{-i H T} \ket{0} = e^{-i E_0 T} \ket{\Omega}\braket{\Omega}{0}
\end{equation}
in the \( T \rightarrow \infty(1 – i \epsilon) \) limit. We can now write the ground state as
\begin{equation}\label{eqn:qftLecture14:360}
\begin{aligned}
\ket{\Omega}
&=
\evalbar{
\frac{ e^{i E_0 T – i H T } \ket{0} }{
\braket{\Omega}{0}
}
}{ T \rightarrow \infty(1 – i \epsilon) } \\
&=
\evalbar{
\frac{ e^{- i H T } \ket{0} }{
e^{-i E_0 T} \braket{\Omega}{0}
}
}{ T \rightarrow \infty(1 – i \epsilon) }.
\end{aligned}
\end{equation}
Shifting the very large \( T \rightarrow T + t_0 \) shouldn’t change things, so
\begin{equation}\label{eqn:qftLecture14:480}
\ket{\Omega}
=
\evalbar{
\frac{ e^{- i H (T + t_0) } \ket{0} }{
e^{-i E_0 (T + t_0) } \braket{\Omega}{0}
}
}{ T \rightarrow \infty(1 – i \epsilon) }.
\end{equation}
A bit of manipulation shows that the operator in the numerator has the structure of a time evolution operator.
Claim: (DIY):
\Cref{eqn:qftLecture14:80}, \ref{eqn:qftLecture14:120} may be generalized to
\begin{equation}\label{eqn:qftLecture14:400}
U(t, t’) = e^{i H_0(t – t_0)} e^{-i H(t – t’)} e^{-i H_0(t’ – t_0)} =
T \exp{\lr{ -i \int_{t’}^t H_{\text{I,int}}(t”) dt”}}.
\end{equation}
Observe that we recover \ref{eqn:qftLecture14:120} when \( t’ = t_0 \). Using \ref{eqn:qftLecture14:400} we find
\begin{equation}\label{eqn:qftLecture14:520}
\begin{aligned}
U(t_0, -T) \ket{0}
&= e^{i H_0(t_0 – t_0)} e^{-i H(t_0 + T)} e^{-i H_0(-T – t_0)} \ket{0} \\
&= e^{-i H(t_0 + T)} e^{-i H_0(-T – t_0)} \ket{0} \\
&= e^{-i H(t_0 + T)} \ket{0},
\end{aligned}
\end{equation}
where we use the fact that \( e^{i H_0 \tau} \ket{0} = \lr{ 1 + i H_0 \tau + \cdots } \ket{0} = 1 \ket{0}, \) since \( H_0 \ket{0} = 0 \).
We are left with
\begin{equation}\label{eqn:qftLecture14:420}
\boxed{
\ket{\Omega}
= \frac{U(t_0, -T) \ket{0} }{e^{-i E_0(t_0 – (-T))} \braket{\Omega}{0}}.
}
\end{equation}
We are close to where we want to be. Wednesday we finish off, and then start scattering and Feynman diagrams.
References
[1] Michael E Peskin and Daniel V Schroeder. An introduction to Quantum Field Theory. Westview, 1995.
[2] Wikipedia contributors. Riemann-lebesgue lemma — Wikipedia, the free encyclopedia, 2018. URL https://en.wikipedia.org/w/index.php?title=Riemann%E2%80%93Lebesgue_lemma&oldid=856778941. [Online; accessed 29-October-2018].