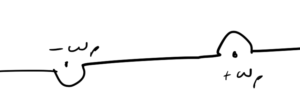[Click here for a PDF of this post with nicer formatting]
DISCLAIMER: Very rough notes from class, with some additional side notes.
These are notes for the UofT course PHY2403H, Quantum Field Theory, taught by Prof. Erich Poppitz, fall 2018.
Green’s functions for the forced Klein-Gordon equation.
The problem were were preparing to do was to study the problem of “particle creation by external classical source”.
We continue with a real scalar field, free, massive, but with an interaction with a source
\begin{equation}\label{eqn:qftLecture12:20}
S_{\text{int}} = \int d^4 x j(x) \phi(x).
\end{equation}
Modern application:
think of \( \phi \) has some SM field and think of \( j \) as due to inflaton (i.e. cosmological inflation interaction) oscillation. In the inflationary model, the process of “reheating” creates all the matter in the universe. We won’t be talking about inflation, but will be considering a toy model that has some similar characteristics to the inflationary theory.
The equation of motion that we end up with is
\begin{equation}\label{eqn:qftLecture12:40}
\lr{ \partial_\mu \partial^\mu + m^2} \phi = j,
\end{equation}
and we wish to solve this using Green’s function techniques.
Definition: Klein-Gordon Green’s function.
The QFT conventions for the Klein-Gordon Green’s function is
\begin{equation*}
\lr{ \partial_\mu \partial^\mu + m^2} G(x – y) = -i \delta^4(x – y).
\end{equation*}
As usual, we assume that it is possible to find a solution \( \phi \) by convolution
\begin{equation}\label{eqn:qftLecture12:80}
\phi(x) = i \int d^4 y G(x – y) j(y).
\end{equation}
Check:
\begin{equation}\label{eqn:qftLecture12:100}
\begin{aligned}
\lr{ \partial_\mu \partial^\mu + m^2} \phi(x)
&=
i
\lr{ \partial_\mu \partial^\mu + m^2}
\int d^4 y G(x – y) j(y) \\
&=
i \int d^4 y (-i) \delta^4(x – y) j(y) \\
&= j(x).
\end{aligned}
\end{equation}
Also, as usual, we take out our Fourier transforms, the power tool of physics, and determine the structure of the Green’s function by inverting the transform equation
\begin{equation}\label{eqn:qftLecture12:120}
G(x – y) = \int \frac{d^4 p}{(2 \pi)^4} e^{-i p \cdot (x-y) } \tilde{G}(p).
\end{equation}
Operating with KG gives
\begin{equation}\label{eqn:qftLecture12:520}
\lr{ \partial_\mu \partial^\mu + m^2}
G(x)
=
\int \frac{d^4 p}{(2 \pi)^4}
\lr{ (-i p_\mu)(-i p^\mu) + m^2 }
e^{-i p \cdot (x-y) } \tilde{G}(p).
\end{equation}
This must equal
\begin{equation}\label{eqn:qftLecture12:140}
-i \delta^4(x – y) =
-i \int \frac{d^4 p}{(2 \pi)^4} e^{-i p \cdot (x -y)},
\end{equation}
or
\begin{equation}\label{eqn:qftLecture12:160}
\lr{ m^2 – p_\mu p^\mu } \tilde{G}(p) = -i.
\end{equation}
The Green’s function in the momentum domain is
\begin{equation}\label{eqn:qftLecture12:180}
\tilde{G}(p) = \frac{i}{p^2 – m^2}.
\end{equation}
The inverse transform provides the spatial domain representation of the Green’s function
\begin{equation}\label{eqn:qftLecture12:200}
\begin{aligned}
G(x)
&=
\int \frac{d^4 p}{(2 \pi)^4} e^{-i p \cdot x }
\frac{i}{(p^0)^2 – \Bp^2 – m^2} \\
&=
\int \frac{d^3 p}{(2\pi)^3} e^{i \Bp \cdot \Bx}
\int \frac{d p_0}{2 \pi} e^{-i p_0 x^0 }
\frac{i}{(p_0 – \omega_\Bp)(p_0 + \omega_\Bp)}.
\end{aligned}
\end{equation}
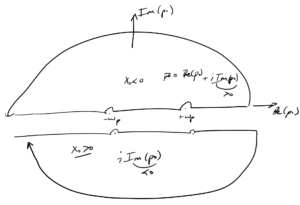
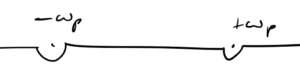
In the \( p_0 \) plane, we have two poles at \( p_0 = \pm \omega_\Bp \). There are 4 ways to go around the poles, the retarded time deformation that we used to derive the Green’s function for the harmonic oscillator, as sketched in fig. 1, the advanced time deformation sketched in fig. 2, and mixed deformations.
fig. 1. Retarded time deformations and contours.
fig. 2. Advanced time deformation.
We will evaluate the integral using the “Feynman propagator” contour sketched in fig. 3. Why we use the Feynman contour, and not the retarded contour can be justified by how well this works for the perturbation methods that will be developed later.
fig. 3. Feynman propagator deformation path.
Consider each contour in turn.
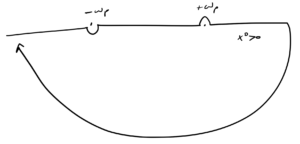
Case I. \( x^0 > 0 \)
For this case, we use the lower half plane contour sketched in fig. 4, which vanishes for \( \Im(p_0) < 0, x_0 > 0 \), where \( -i (i \Im(p_0) x_0) < 0 \).
fig. 4. Feynman propagator contour for t > 0.
Here we pick up just the pole at \( p_0 = \omega_\Bp \), and take a negatively oriented path
\begin{equation}\label{eqn:qftLecture12:220}
\begin{aligned}
G_\txtF
&=
\int \frac{d^3 p}{(2\pi)^3} e^{i \Bp \cdot \Bx}
\int \frac{d p_0}{2 \pi} e^{-i p_0 x^0 }
\frac{i}{(p_0 – \omega_\Bp)(p_0 + \omega_\Bp)} \\
&=
\int \frac{d^3 p}{(2\pi)^3} e^{i \Bp \cdot \Bx}
(-2 \pi i)
\evalbar{\lr{ \frac{e^{-i p_0 x^0 }}{2 \pi}
\frac{i}{p_0 + \omega_\Bp} }}{p_0 = \omega_p} \\
&=
\int \frac{d^3 p}{(2\pi)^3} e^{i \Bp \cdot \Bx}
\frac{-2 \pi i}{2 \pi} \frac{i e^{-i p_0 x^0 } }{2 \omega_\Bp} \\
&=
\int \frac{d^3 p}{(2\pi)^3} e^{i \Bp \cdot \Bx}
\frac{ e^{-i \omega_\Bp x^0 } }{2 \omega_\Bp}.
\end{aligned}
\end{equation}
Case II. \( x^0 < 0 \)
For \( x^0 < 0 \) we use an upper half plane contour with the same deformation around the poles. This time
\begin{equation}\label{eqn:qftLecture12:240}
\begin{aligned}
G_\txtF
&=
\int \frac{d^3 p}{(2\pi)^3} e^{i \Bp \cdot \Bx}
\int \frac{d p_0}{2 \pi} e^{-i p_0 x^0 }
\frac{i}{(p_0 – \omega_\Bp)(p_0 + \omega_\Bp)} \\
&=
\int \frac{d^3 p}{(2\pi)^3} e^{i \Bp \cdot \Bx}
(+ 2 \pi i)
\evalbar{\lr{\frac{e^{-i p_0 x^0 }}{2 \pi}
\frac{i}{p_0 – \omega_\Bp}}}{p_0 = -\omega_\Bp} \\
&=
\int \frac{d^3 p}{(2\pi)^3} e^{i \Bp \cdot \Bx}
\frac{+2 \pi i}{2 \pi} \frac{i e^{-i p_0 x^0 } }{-2 \omega_\Bp} \\
&=
\int \frac{d^3 p}{(2\pi)^3} e^{i \Bp \cdot \Bx}
\frac{ e^{i \omega_\Bp x^0 } }{2 \omega_\Bp}.
\end{aligned}
\end{equation}
We’ve obtained a piecewise representation of the Green’s function, where the only difference is the sign of the \( i \omega_\Bp x^0 \) exponential.
We can combine \ref{eqn:qftLecture12:220} \ref{eqn:qftLecture12:240} by using \( \Theta \) functions
\begin{equation}\label{eqn:qftLecture12:260}
\int \frac{d^3 p}{(2\pi)^3 2 \omega_\Bp} e^{i \Bp \cdot \Bx}
\lr{
e^{-i \omega_\Bp x^0 } \Theta(x_0)
+
e^{i \omega_\Bp x^0 } \Theta(-x_0)
}.
\end{equation}
The first integral (without the \(\Theta\) factor) is the Weightmann function
\begin{equation}\label{eqn:qftLecture12:280}
D(x)
=
\int \frac{d^3 p}{(2\pi)^3 2 \omega_\Bp} \evalbar{e^{-i p \cdot x}}{p^0 = \omega_\Bp}.
\end{equation}
For the second integral, we make a change of variables \( \Bp \rightarrow -\Bp \) leaving
\begin{equation}\label{eqn:qftLecture12:300}
\begin{aligned}
\int \frac{d^3 p}{(2\pi)^3 2 \omega_\Bp} e^{i \Bp \cdot \Bx + i \omega_\Bp x^0}
&\rightarrow
\int \frac{d^3 p}{(2\pi)^3 2 \omega_\Bp} e^{-i \Bp \cdot \Bx + i \omega_\Bp x^0} \\
&=
\int \frac{d^3 p}{(2\pi)^3 2 \omega_\Bp} e^{-i p \cdot x} \\
&= D(-x),
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:qftLecture12:340}
\boxed{
G_\txtF (x) = \Theta(x^0) D(x) + \Theta(-x^0) D(-x)
}
\end{equation}
Matrix element representation of the Weightmann function.
Recall that the Weightmann function also had a matrix element representation
\begin{equation}\label{eqn:qftLecture12:360}
D(x) = \bra{0} \phi(x) \phi(0) \ket{0}.
\end{equation}
This can be shown by expansion.
\begin{equation}\label{eqn:qftLecture12:380}
\bra{0} \phi(x) \phi(0) \ket{0}
=
\bra{0}
\int \frac{d^3 p}{(2 \pi)^3} \inv{\sqrt{2 \omega_\Bp}} \evalbar{\lr{ a_\Bp e^{-i p \cdot x} + a_\Bp^\dagger e^{i p \cdot x} }}{p_0 = \omega_\Bp}
\int \frac{d^3 q}{(2 \pi)^3} \inv{\sqrt{2 \omega_\Bq}} \lr{ a_\Bq^\dagger + a_\Bq }
\ket{0}
\end{equation}
Since \( a_\Bq \ket{0} = 0 = \bra{0} a_\Bp^\dagger \), \ref{eqn:qftLecture12:380}
reduces to
\begin{equation}\label{eqn:qftLecture12:540}
\begin{aligned}
\bra{0} \phi(x) \phi(0) \ket{0}
&=
\bra{0}
\int
\frac{d^3 p}{(2 \pi)^3}
\frac{d^3 q}{(2 \pi)^3}
\inv{\sqrt{2 \omega_\Bp}}
\inv{\sqrt{2 \omega_\Bq}}
\evalbar{\lr{ a_\Bp a_\Bq^\dagger e^{-i p \cdot x} }}{p_0 = \omega_\Bp}
\ket{0} \\
&=
\bra{0}
\int
\frac{d^3 p}{(2 \pi)^3}
\frac{d^3 q}{(2 \pi)^3}
\inv{\sqrt{2 \omega_\Bp}}
\inv{\sqrt{2 \omega_\Bq}}
\evalbar{\lr{
\lr{
a_\Bp
a_\Bq^\dagger
+
\antisymmetric{
a_\Bp
}{
a_\Bq^\dagger
}
}
e^{-i p \cdot x} }}{p_0 = \omega_\Bp}
\ket{0} \\
&=
\bra{0}
\int
\frac{d^3 p}{(2 \pi)^3}
\frac{d^3 q}{(2 \pi)^3}
\inv{\sqrt{2 \omega_\Bp}}
\inv{\sqrt{2 \omega_\Bq}}
\evalbar{\lr{
\lr{
(2 \pi)^3 \delta^3(\Bp – \Bq)
}
e^{-i p \cdot x} }}{p_0 = \omega_\Bp} \\
&=
\int \frac{d^3 p}{(2 \pi)^3} \evalbar{ \frac{e^{-i p \cdot x}}{2 \omega_\Bp} }
{p_0 = \omega_\Bp}
\end{aligned}
\end{equation}
Retarded Green’s function.
Claim: Retarded Green’s function (bumps up contour) can be written
\begin{equation}\label{eqn:qftLecture12:400}
D_R(x) = \theta(x_0) (D(x) – D(-x)).
\end{equation}
Proof: The upper half plane contour (\(x_0 < 0\)) is zero since it encloses no poles. For the lower half plane contour we have \begin{equation}\label{eqn:qftLecture12:420} \begin{aligned} \evalbar{D_R(x)}{x_0 > 0}
&=
i \int \frac{d^3 p}{(2 \pi)^3} e^{i \Bp \cdot \Bx} \int \frac{dp_0}{2 \pi} e^{-i p_0 x^0 }
\frac{i}{(p_0 – \omega_\Bp)(p_0 + \omega_\Bp)} \\
&=
i \int \frac{d^3 p}{(2 \pi)^3} e^{i \Bp \cdot \Bx} \frac{(-2 \pi i)}{2 \pi}
\lr{
e^{-i \omega_\Bp x^0 }
\frac{i}{2 \omega_\Bp}
+
e^{i \omega_\Bp x^0 }
\frac{i}{-2 \omega_\Bp}
} \\
&=
\int \frac{d^3 p}{(2 \pi)^3} e^{i \Bp \cdot \Bx}
\frac{1}{2 \omega_\Bp}
\lr{
e^{-i \omega_\Bp x^0 }
–
e^{i \omega_\Bp x^0 }
} \\
&=
D(x) – D(-x).
\end{aligned}
\end{equation}
What does the field look like in terms of the propagator? Assuming that \( \phi_0 \) satisfies the homogeneous equation, we have
\begin{equation}\label{eqn:qftLecture12:440}
\begin{aligned}
\phi(x)
&= \phi_0(x) + i \int d^4 y D_R(x – y) j(y) \\
&= \phi_0(x) + i \int d^3 y d y_0 \Theta(x_0 – y_0) \lr{ D(x – y) – D(y – x) } j(y)
\end{aligned}
\end{equation}
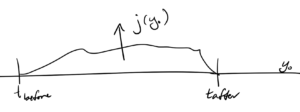
Imagine that we have a windowed source function \( j(y^0, \By) \), as sketched in fig. 5.
fig. 5. Finite window impulse response.
\begin{equation}\label{eqn:qftLecture12:460}
\evalbar{\phi(x)}{x^0 > t_{\text{after}}}
= \phi_0(x)
+ i \int d^4 y
\lr{
\int \frac{d^3 p}{(2\pi)^3 2 \omega_\Bp } e^{-i p \cdot (x – y)} j(y)
–
\int \frac{d^3 p}{(2\pi)^3 2 \omega_\Bp } e^{i p \cdot (x – y)} j(y)
}
\end{equation}
define
\begin{equation}\label{eqn:qftLecture12:480}
\tilde{j}(p) = \int d^4 y e^{i p \cdot y} j(y),
\end{equation}
which gives
\begin{equation}\label{eqn:qftLecture12:500}
\evalbar{\phi(x)}{x^0 > t_{\text{after}}}
= \phi_0(x)
+ i \int \frac{d^3 p }{(2 \pi)^3}
\inv{
2 \omega_\Bp }
\evalbar{
\lr{
e^{-i p \cdot x} \tilde{j}(p)
– e^{i p \cdot x} \tilde{j}(-p)
}
}{p_0 = \omega_\Bp}.
\end{equation}
We will interpret this in the next lecture, and start in on Feynman diagrams.