This post contains a summary of my lecture notes for the second half of last Wednesday’s QFT-I lecture.
[Click here for a PDF with the full notes for this portion of the lecture.]
DISCLAIMER: Very rough notes from class, with some additional side notes.
These are notes for the UofT course PHY2403H, Quantum Field Theory, taught by Prof. Erich Poppitz, fall 2018.
Summary:
- We found that the Dirac Hamiltonian is
\begin{equation*}
H
=
\int d^3 x
\Psi^\dagger
\lr{
– i \gamma^0 \gamma^j \partial_j \Psi + m \gamma^0
}
\Psi.
\end{equation*} - We found that our plane wave solutions
\(\Psi_u = u(p) e^{-i p \cdot x}\), and \( \Psi_v = v(p) e^{i p \cdot x} \), were eigenvectors of the operator portion of the Hamiltonian
\begin{equation*}
\begin{aligned}
-\gamma^0 \lr{ i \gamma^j \partial_j – m } \Psi_u &= p_0 \Psi_u \\
-\gamma^0 \lr{ i \gamma^j \partial_j – m } \Psi_v &= -p_0 \Psi_v.
\end{aligned}
\end{equation*} - We formed a linear superposition of our plane wave solutions
\begin{equation}\label{eqn:qftLecture21b:800}
\Psi(\Bx, t)
=
\sum_{s = 1}^2
\int \frac{d^3 p}{(2 \pi)^3 \sqrt{ 2 \omega_\Bp } }
\lr{
e^{-i p \cdot x} u^s_\Bp a_\Bp^s
+
e^{i p \cdot x} v^s_\Bp b_\Bp^s
}.
\end{equation} - and expressed the Dirac Hamiltonian in terms of creation and anhillation operators
\begin{equation*}
H_{\text{Dirac}}
=
\sum_{r = 1}^2
\int \frac{d^3 p }{(2\pi)^3 }
\omega_\Bp
\lr{
a^{r \dagger}_\Bp
a^r_\Bp
–
b^{r \dagger}_{-\Bp}
b^r_{-\Bp}
}.
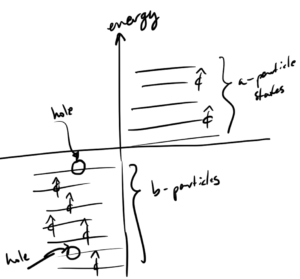
\end{equation*} - Finally, we interpreted this using the Dirac Sea argument
- It was claimed that the \( a, b\)’s satisfied anticommutator relationships
\begin{equation}\label{eqn:qftLecture21b:940}
\begin{aligned}
\symmetric{a^s_\Bp}{a^{r \dagger}_\Bq} &= \delta^{sr} \delta^{(3)}e(\Bp – \Bq) \\
\symmetric{b^s_\Bp}{b^{r \dagger}_\Bq} &= \delta^{sr} \delta^{(3)}(\Bp – \Bq),
\end{aligned}
\end{equation}
where all other anticommutators are zero
\begin{equation}\label{eqn:qftLecture21b:960}
\symmetric{a^r}{b^s} =
\symmetric{a^r}{b^{s\dagger}} =
\symmetric{a^{r\dagger}}{b^s} =
\symmetric{a^{r\dagger}}{b^{s\dagger}} = 0.
\end{equation}
and used these to algebraically remove the negative energy states of the Hamiltonian.