[Click here for a PDF version of this post]

Motivation

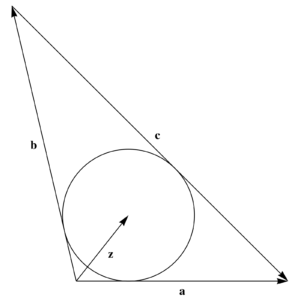
In Jim Smith’s recent Handling Rejection! Using Geometric Algebra to Find the Incircle of a Triangle video, he uses an area argument to find the center point of a circle inscribed in a triangle, as illustrated in fig. 1.

fig. 1. Triangle with inscribed circle.

fig. 1. Triangle with inscribed circle.

In the video, Jim mentioned that he first tried calculating the intersection of the bivectors, but didn’t like the form of the solution. I’m curious what aspect of that solution wasn’t desirable, since it is a pretty compact way to solve the system.

Setup.

A very convenient way to describe a triangle is with a pair of vectors for two of the edges, say \( \Ba, \Bb \), where the third edge is \( \Bc = \Ba -\Bb \). In Jim’s problem, he started with the scalar lengths of all the edges \( a, b, c \). The two representations are interchangable. We can set
\begin{equation}\label{eqn:triangleInscribedCircle:n}\
\begin{aligned}
\Ba &= a\Be_1 \\
\Bb &= b \Be_1 e^{i\theta_c},
\end{aligned}
\end{equation}
where \( i = \Be_1 \Be_2 \), and \( \theta_c \) is the angle opposite edge \( \Bc \), which can be found from the cosine law
\begin{equation}\label{eqn:triangleInscribedCircle:20}
\Bc^2 = \lr{ \Ba – \Bb }^2 = \Ba^2 + \Bb^2 – 2 \Ba \cdot \Bb = a^2 + b^2 – 2 a b \cos\theta_c,
\end{equation}
or
\begin{equation}\label{eqn:triangleInscribedCircle:40}
\theta_c = \cos^{-1} \lr{ \frac{a^2 + b^2 – c^2}{2 a b} }.
\end{equation}

The center point.

The points on our bisectors are
\begin{equation}\label{eqn:triangleInscribedCircle:60}
\begin{aligned}
r_c(t) &= t \lr{ \mathbf{\hat{a}} + \mathbf{\hat{b}} } \\
r_b(t) &= \Ba + t \lr{ \mathbf{\hat{a}} + \mathbf{\hat{c}} } \\
r_a(t) &= \Bb + t \lr{ \mathbf{\hat{c}} – \mathbf{\hat{b}} }.
\end{aligned}
\end{equation}
We can find the intersection of any two of these to find the center point of the circle. For example, we seek solutions of
\begin{equation}\label{eqn:triangleInscribedCircle:80}
u \lr{ \mathbf{\hat{a}} + \mathbf{\hat{b}} } = \Ba + v \lr{ \mathbf{\hat{a}} + \mathbf{\hat{c}} }.
\end{equation}
We can wedge this with either of the \( u, v \) vector factors, to eliminate one of the scalars in this equation. Seeking \( u \), we wedge with \( \mathbf{\hat{a}} + \mathbf{\hat{c}} \), for
\begin{equation}\label{eqn:triangleInscribedCircle:100}
u \lr{ \mathbf{\hat{a}} + \mathbf{\hat{c}} } \wedge \lr{ \mathbf{\hat{a}} + \mathbf{\hat{b}} } = \lr{ \mathbf{\hat{a}} + \mathbf{\hat{c}} } \wedge \Ba = \mathbf{\hat{c}} \wedge \Ba.
\end{equation}
so
\begin{equation}\label{eqn:triangleInscribedCircle:120}
\Bz = \lr{ \mathbf{\hat{a}} + \mathbf{\hat{b}} } \lr{ \lr{ \mathbf{\hat{c}} \wedge \Ba } \cdot \inv{ \lr{ \mathbf{\hat{a}} + \mathbf{\hat{c}} } \wedge \lr{ \mathbf{\hat{a}} + \mathbf{\hat{b}} } } }.
\end{equation}
Having found the center, we can calculate the radius that touches the \( a \) edge, which is just
\begin{equation}\label{eqn:triangleInscribedCircle:140}
\mathrm{Rej}_{\Ba}(\Bz) = \lr{ \Bz \wedge \mathbf{\hat{a}} } \cdot \mathbf{\hat{a}}.
\end{equation}
The scalar radius is
\begin{equation}\label{eqn:triangleInscribedCircle:160}
r = \Norm{ \Bz \wedge \mathbf{\hat{a}} }.
\end{equation}

Calculation.

Using a Mathematica Manipulate, I plotted this solution, employing a duality transformation to calculate the bivectors using cross products (avoiding any GA package dependencies.)

For the radius, we need only:
\begin{equation}\label{eqn:triangleInscribedCircle:200}
r = \Norm{ \Bz \cross \mathbf{\hat{a}} }.
\end{equation}

For the intersection, we can use:
\begin{equation}\label{eqn:triangleInscribedCircle:180}
\Bz = \lr{ \mathbf{\hat{a}} + \mathbf{\hat{b}} } \lr{ \lr{ \mathbf{\hat{c}} \cross \Ba } \cdot \inv{ \lr{ \mathbf{\hat{a}} + \mathbf{\hat{c}} } \cross \lr{ \mathbf{\hat{a}} + \mathbf{\hat{b}} } } }.
\end{equation}

In retrospect, just using a ratio of the determinants of the coordinates would have been a direct representation of the ratio of the wedge products, so I could have done that instead to translate the results from GA to Mathematica (since this is a planar problem.)  The wedge products could have also been encoding using complex numbers (in the newest version of the notebook, I’ve done that.)


Of course, using Mathematica, we could have just used it’s more general \( \textrm{Solve} \) function, and need not grow our own wedge product based implementation.