[Click here for a PDF version of this post]

One of my favorite Dover books, [1], is a powerhouse of a reference, and has a huge set of the mathematical tricks and techniques.  Probably most of the tricks that any engineer or physicist would ever want.

Reading it a bit today, I encountered the following interesting looking theorem for evaluating sums using contour integrals.

Theorem 1.1:

Given a meromorphic function \( f(z) \) that shares no poles with \( \cot( \pi z ) \), where \( C \) encloses the zeros of \( \sin( \pi z \), located at \( z = a, a+1, \cdots b \), then
\begin{equation*}
\sum_{m=a}^b f(m) = \inv{2 \pi i} \oint_C \pi \cot( \pi z ) f(z) dz -\quad \sum_{\mbox{poles of \( f(z) \) in \( C \)}} \mathrm{Res}\lr{ \pi \cot( \pi z ) f(z) }.
\end{equation*}

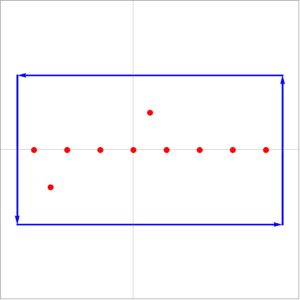
The enclosing contour may look like fig. 1.

fig. 1. Sample contour

Start proof:

We basically want to evaluate
\begin{equation}\label{eqn:sumUsingContour:20}
\oint_C \pi \cot( \pi z ) f(z) dz,
\end{equation}
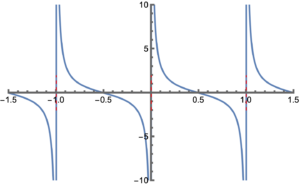
using residues. To see why this works, observe that \( \cot( \pi z ) \) is periodic, as plotted in fig. 2.

fig. 2. Cotangent.

In particular, if \( z = m + \epsilon \), we have
\begin{equation}\label{eqn:sumUsingContour:40}
\begin{aligned}
\cot(\pi z)
&= \frac{\cos(\pi(m + \epsilon))}{\sin(\pi(m + \epsilon))} \\
&= \frac{(-1)^m \cos(\pi \epsilon)}{(-1)^m \sin(\pi \epsilon)} \\
&= \cot(\pi \epsilon).
\end{aligned}
\end{equation}
The residue of \( \pi \cot(\pi z) \), at \( z = 0 \), or at any other integer point, is
\begin{equation}\label{eqn:sumUsingContour:60}
\frac{\pi}{
\pi z – (\pi z)^3/6 + \cdots
}
= 1.
\end{equation}
This means that we have
\begin{equation}\label{eqn:sumUsingContour:80}
\oint_C \pi \cot( \pi z ) f(z) dz = 2 \pi i \sum_{m = a}^b f(m) + 2 \pi i \quad \sum_{\mbox{poles of \( f(z) \) in \( C \)}} \mathrm{Res}\lr{ \pi \cot( \pi z ) f(z) }.
\end{equation}
We just have to rearrange and scale to complete the proof.

End proof.

In the book the sample application was to use this to show that
\begin{equation}\label{eqn:sumUsingContour:100}
\coth x – \inv{x} = \sum_{m=1}^\infty \frac{2x}{x^2 + m^2 \pi^2}.
\end{equation}
That’s then integrated to show that
\begin{equation}\label{eqn:sumUsingContour:120}
\frac{\sinh x}{x} = \prod_{m = 1}^\infty \lr{ 1 + \frac{x^2}{m^2 \pi^2} },
\end{equation}
or with \( x = i \theta \),
\begin{equation}\label{eqn:sumUsingContour:140}
\sin \theta = \theta \prod_{m = 1}^\infty \lr{ 1 – \frac{\theta^2}{m^2 \pi^2} },
\end{equation}
and finally equating \( \theta^3 \) terms in this infinite product, we find
\begin{equation}\label{eqn:sumUsingContour:160}
\sum_{m = 1}^\infty \inv{m^2} = \frac{\pi^2}{6},
\end{equation}
which is \( \zeta(2) \), a specific value of the Riemann zeta function.

All this is done in a couple spectacularly dense pages of calculation, and illustrates the kind of gems in this book. At about 700 pages, it’s got a lot of gems.

References

[1] F.W. Byron and R.W. Fuller. Mathematics of Classical and Quantum Physics. Dover Publications, 1992.