Month: April 2025

toycalculator, an MLIR/LLVM compiler experiment.

April 27, 2025 C/C++ development and debugging. No comments , , , , ,

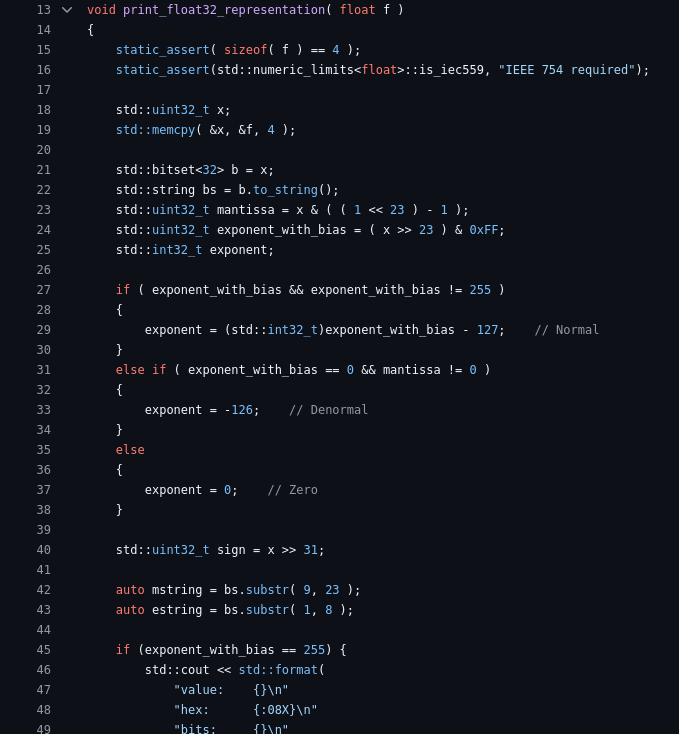
Over the last 8 years, I’ve been intimately involved in building a pair of LLVM based compilers for the COBOL and PL/I languages.  However, a lot of my work was on the runtime side of the story. This was non-trivial work, with lots of complex interactions to figure out, but it also meant that I didn’t get to play with the fun (codegen) part of the compiler.

Over the last month or so, I’ve been incrementally building an MLIR based compiler for a toy language.  I thought this would be a great way to get my hands dirty, and learn as I went.  These were the elements required:

As it turns out, MLIR tablegen is pretty finicky when you have no clue what you are doing.  Once you get the basic infrastructure in place it makes a lot more sense, and you can look at the generated C++ classes associated with your tablegen, to get a good idea what is happening under the covers.

Here’s a couple examples that illustrate the toy language:

// empty.toy
// This should be allowed by the grammar.



// dcl.toy
DCL x; // the next simplest non-empty program (i.e.: also has a comment)



// foo.toy
DCL x;
x = 3;
// This indenting is to test location generation, and to verify that the resulting columnar position is right.
     PRINT x;



// unary.toy
DCL x;
x = 3;
x = +x;
x = -x;
PRINT x;



// test.toy
DCL x;
DCL y;
x = 5 + 3;
y = x * 2;
PRINT x;

There is also a RETURN statement, not in any of those examples explicitly. I added that language element to simplify the LLVM lowering process. Here’s a motivating example:

> ../build/toycalculator empty.toy  --location
"builtin.module"() ({
  "toy.program"() ({
  ^bb0:
  }) : () -> () loc(#loc1)
}) : () -> () loc(#loc)
#loc = loc(unknown) 
#loc1 = loc("empty.toy":2:1)

Notice the wierd looking ‘^bb0:’ in the MLIR dump. This is a representation of an empty basic block, and was a bit of a pain to figure out how to lower properly. What I ended up doing is inserting a RETURN operation into the program if there was no other statements. I wanted to support such a dumb trivial program with no actual statements as a first test for the lowering, and see that things worked end to end before getting some of the trickier lowering working. With a return statement, empty.toy’s MLIR now looks like:

"builtin.module"() ({ 
  "toy.program"() ({
    "toy.return"() : () -> () loc(#loc1)
  }) : () -> () loc(#loc1)
}) : () -> () loc(#loc)
#loc = loc(unknown)
#loc1 = loc("../samples/empty.toy":2:1)

The idea behind the lowering operations is that each MLIR operation can be matched with a rewriter operation, and the program can be iterated over, gradually replacing all the MLIR operators with LLVM operations.

For example, an element like:

"toy.return"() : () -> ()

Can be replaced by

  %0 = "llvm.mlir.constant"() <{value = 0 : i32}> : () -> i32
  "llvm.return"(%0) : (i32) -> ()

Once that replacement is made, we can delete the toy.return element:

    // Lower toy.return to nothing (erase).
    class ReturnOpLowering : public ConversionPattern
    {
       public:
        ReturnOpLowering( MLIRContext* context )
            : ConversionPattern( toy::ReturnOp::getOperationName(), 1, context )
        {
        }           

        LogicalResult matchAndRewrite(
            Operation* op, ArrayRef operands,
            ConversionPatternRewriter& rewriter ) const override
        {   
            LLVM_DEBUG( llvm::dbgs()
                        << "Lowering toy.return: " << *op << '\n' );
            // ...
            rewriter.eraseOp( op );
            return success();
        }
    };

In the sample above the toy.program elememt also needs to be deleted. It gets replaced by a llvm basic block, moving all the MLIR BB elements into it. The last step is the removal of the outer most MLIR module, but there's an existing Dialect for that. When all is said and done, we are left with the following LLVM IR:

define i32 @main() {
  ret i32 0
}

Here's the MLIR for the foo.toy, which is slightly more interesting

"builtin.module"() ({
  "toy.program"() ({
    %0 = "memref.alloca"() <{operandSegmentSizes = array}> : () -> memref
    "toy.declare"() <{name = "x"}> : () -> ()
    %1 = "arith.constant"() <{value = 3 : i64}> : () -> i64
    %2 = "toy.unary"(%1) <{op = "+"}> : (i64) -> f64
    "memref.store"(%2, %0) : (f64, memref) -> ()
    "toy.assign"(%2) <{name = "x"}> : (f64) -> ()
    "toy.print"(%0) : (memref) -> ()
    "toy.return"() : () -> ()
  }) : () -> ()
}) : () -> ()

As we go through the lowering replacements, more an more of the MLIR operators get replaced with LLVM equivalents. Here's an example part way through:

"llvm.func"() <{CConv = #llvm.cconv, function_type = !llvm.func, linkage = #llvm.linkage, sym_name = "main", visibility_ = 0 : i64}> ({
  %0 = "llvm.mlir.constant"() <{value = 1 : i64}> : () -> i64
  %1 = "llvm.alloca"(%0) <{alignment = 8 : i64, elem_type = f64}> : (i64) -> !llvm.ptr
  %2 = "memref.alloca"() <{operandSegmentSizes = array}> : () -> memref
  "toy.declare"() <{name = "x"}> : () -> ()
  %3 = "llvm.mlir.constant"() <{value = 3 : i64}> : () -> i64
  %4 = "arith.constant"() <{value = 3 : i64}> : () -> i64
  %5 = "toy.unary"(%4) <{op = "+"}> : (i64) -> f64
  "memref.store"(%5, %2) : (f64, memref) -> ()
  "toy.assign"(%5) <{name = "x"}> : (f64) -> ()
  "toy.print"(%2) : (memref) -> ()
  "toy.return"() : () -> ()
}) : () -> ()

and after a few more:

"llvm.func"() <{CConv = #llvm.cconv, function_type = !llvm.func, linkage = #llvm.linkage, sym_na
me = "main", visibility_ = 0 : i64}> ({
  %0 = "llvm.mlir.constant"() <{value = 1 : i64}> : () -> i64
  %1 = "llvm.alloca"(%0) <{alignment = 8 : i64, elem_type = f64}> : (i64) -> !llvm.ptr
  %2 = "memref.alloca"() <{operandSegmentSizes = array}> : () -> memref
  "toy.declare"() <{name = "x"}> : () -> ()
  %3 = "llvm.mlir.constant"() <{value = 3 : i64}> : () -> i64
  %4 = "arith.constant"() <{value = 3 : i64}> : () -> i64
  %5 = "llvm.sitofp"(%3) : (i64) -> f64
  %6 = "toy.unary"(%4) <{op = "+"}> : (i64) -> f64
  "llvm.store"(%5, %1) <{ordering = 0 : i64}> : (f64, !llvm.ptr) -> ()
  "memref.store"(%6, %2) : (f64, memref) -> ()
  "toy.assign"(%6) <{name = "x"}> : (f64) -> ()
  %7 = "llvm.load"(%1) <{ordering = 0 : i64}> : (!llvm.ptr) -> f64
  "llvm.call"(%7) <{CConv = #llvm.cconv, TailCallKind = #llvm.tailcallkind, callee = @__toy_print, fastmathFlags = #llvm.fastmath, op_bundle_sizes = array, operandSegmentSizes = array}> : (f64) -> ()
  "toy.print"(%2) : (memref) -> ()
  %8 = "llvm.mlir.constant"() <{value = 0 : i32}> : () -> i32
  "llvm.return"(%8) : (i32) -> ()
  "toy.return"() : () -> ()
}) : () -> ()

Eventually, after various LLVM IR blocks get merged (almost magically by one of the passes), we end up with:

declare void @__toy_print(double)

define i32 @main() {
  %1 = alloca double, i64 1, align 8
  store double 3.000000e+00, ptr %1, align 8
  %2 = load double, ptr %1, align 8
  call void @__toy_print(double %2)
  ret i32 0
}

Enabling an assembly printer pass, we get an object file

fedora:/home/pjoot/toycalculator/samples> objdump -dr foo.o

foo.o:     file format elf64-x86-64


Disassembly of section .text:

0000000000000000 
:
   0:   50                      push   %rax
   1:   48 b8 00 00 00 00 00    movabs $0x4008000000000000,%rax
   8:   00 08 40 
   b:   48 89 04 24             mov    %rax,(%rsp)
   f:   f2 0f 10 05 00 00 00    movsd  0x0(%rip),%xmm0        # 17 
  16:   00 
                        13: R_X86_64_PC32       .LCPI0_0-0x4
  17:   e8 00 00 00 00          call   1c 
                        18: R_X86_64_PLT32      __toy_print-0x4
  1c:   31 c0                   xor    %eax,%eax
  1e:   59                      pop    %rcx
  1f:   c3                      ret

Here's an end to end example of a full compile, link and build of this little module:

fedora:/home/pjoot/toycalculator/samples> ../build/toycalculator foo.toy 
Generated object file: foo.o
fedora:/home/pjoot/toycalculator/samples> clang -o foo foo.o -L ../build -l toy_runtime -Wl,-rpath,`pwd`/../build
fedora:/home/pjoot/toycalculator/samples> ./foo
3.000000

A month of work and 1800 lines of code, and now I can print a single constant number!

A little float explorer program

April 23, 2025 C/C++ development and debugging. No comments , , , ,

Karl’s 1st year C programming course included IEEE floating point representation.  It’s good to understand that representation, but pretty silly to try to do those conversions by hand.

I remember covering this in our computer organization course, but by that time I’d already figured it out for my own purposes.  I wasn’t smart enough to look it up, and figured it out the hard way by reverse engineering the layout with printfs or the debugger or something like that.

I couldn’t help myself and wrote a little program to unpack a (32-bit) float into it’s representative parts.  The idea is that we have a number in the form:

\begin{equation}\label{eqn:float32:1}
\pm 1.bbbbbbbb x 2^n
\end{equation}

The sizes of those components in a 32-bit C float type are:

  • 1 sign bit,
  • 8 exponent bits,
  • 1 implied 1 mantissa bit,
  • 23 mantissa bits,

where the exponent has a bias (127 = (1<<7)-1) so that the hardware doesn’t have to do any twos complement manipulation.

I’ve put my little floating point explorer program on github. Here is some sample output:

value:    0
hex:      00000000
bits:     00000000000000000000000000000000
sign:     0
exponent:  00000000                        (0+0)
mantissa:          00000000000000000000000
number:          0.00000000000000000000000 x 2^(0)

value:    inf
hex:      7F800000
bits:     01111111100000000000000000000000
sign:     0
exponent:  11111111
mantissa:          00000000000000000000000
number:   +inf

value:    -inf
hex:      FF800000
bits:     11111111100000000000000000000000
sign:     1
exponent:  11111111
mantissa:          00000000000000000000000
number:   -inf

value:    nan
hex:      7FC00000
bits:     01111111110000000000000000000000
sign:     0
exponent:  11111111
mantissa:          10000000000000000000000
number:   NaN

value:    1.1754944e-38
hex:      00800000
bits:     00000000100000000000000000000000
sign:     0
exponent:  00000001                        (127 -126)
mantissa:          00000000000000000000000
number:          1.00000000000000000000000 x 2^(-126)

value:    3.4028235e+38
hex:      7F7FFFFF
bits:     01111111011111111111111111111111
sign:     0
exponent:  11111110                        (127 +127)
mantissa:          11111111111111111111111
number:          1.11111111111111111111111 x 2^(127)
Smallest denormal:

value:    1e-45
hex:      00000001
bits:     00000000000000000000000000000001
sign:     0
exponent:  00000000                        (0-126)
mantissa:          00000000000000000000001
number:          0.00000000000000000000001 x 2^(-126)
Largest denormal:

value:    1.1754942e-38
hex:      007FFFFF
bits:     00000000011111111111111111111111
sign:     0
exponent:  00000000                        (0-126)
mantissa:          11111111111111111111111
number:          0.11111111111111111111111 x 2^(-126)

value:    1
hex:      3F800000
bits:     00111111100000000000000000000000
sign:     0
exponent:  01111111                        (127 +0)
mantissa:          00000000000000000000000
number:          1.00000000000000000000000 x 2^(0)

value:    -2
hex:      C0000000
bits:     11000000000000000000000000000000
sign:     1
exponent:  10000000                        (127 +1)
mantissa:          00000000000000000000000
number:         -1.00000000000000000000000 x 2^(1)

value:    6
hex:      40C00000
bits:     01000000110000000000000000000000
sign:     0
exponent:  10000001                        (127 +2)
mantissa:          10000000000000000000000
number:          1.10000000000000000000000 x 2^(2)

value:    1.5
hex:      3FC00000
bits:     00111111110000000000000000000000
sign:     0
exponent:  01111111                        (127 +0)
mantissa:          10000000000000000000000
number:          1.10000000000000000000000 x 2^(0)

value:    0.125
hex:      3E000000
bits:     00111110000000000000000000000000
sign:     0
exponent:  01111100                        (127 -3)
mantissa:          00000000000000000000000
number:          1.00000000000000000000000 x 2^(-3)

Shoutout to Grok for the code review and the code fragments required to show the representation of NaN, \( \pm \infty \), and denormalized numbers. Grok offered to help extend this to double and long double representations, but where is the fun in letting it do that — that’s an exercise for another day.

EDIT: I updated the code with double decoding support too (and added command line options):

./floatexplorer  --float --double 1
value:    1
hex:      3F800000
bits:     00111111100000000000000000000000
sign:     0
exponent:  01111111                        (127 +0)
mantissa:          00000000000000000000000
number:          1.00000000000000000000000 x 2^(0)

value:    1
hex:      3FF0000000000000
bits:     0011111111110000000000000000000000000000000000000000000000000000
sign:     0
exponent:  01111111111                                                     (1023 +0)
mantissa:             0000000000000000000000000000000000000000000000000000
number:             1.0000000000000000000000000000000000000000000000000000 x 2^(0)

more git-fu: reset –hard after force push

April 10, 2025 Linux , , ,

When I have a branch that I’m sharing only between myself, it’s occasionally helpful to force push and then reset all the other repo versions of the branch to the new one.  Yes, I know that’s inherently dangerous, and I’ve screwed up doing this a couple times.

Here’s one way to do it:

# alias gitbranch='git branch --show-current'
git fetch
git reset origin/`gitbranch` --hard

When I do this, I always first check that the branch on the repo in question is pushed to the upstream branch (i.e., I can consider the current state discardable), and sometimes I’ll also do a sanity check diff against the commit hash that came with the fetch to see what I’m going to get with the reset.

Assuming that I still want to be stupid and dangerous, is there an easier way to do it?

I asked Grok if there was an short cut for this action, and as expected, there’s a nice one:

git fetch
git reset @{u} --hard

Here the @{u} is a shorthand for the current upstream branch.

Grok suggested a one liner using && for the two commands, but when I’m being dangerous and (possibly) stupid I’d rather be more deliberate and do these separately, so that I can think between the two steps.