ECE1254H Modeling of Multiphysics Systems. Lecture 2: Assembling system equations automatically. Taught by Prof. Piero Triverio

September 23, 2014 ece1254 , ,

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

Assembling system equations automatically. Node/branch method

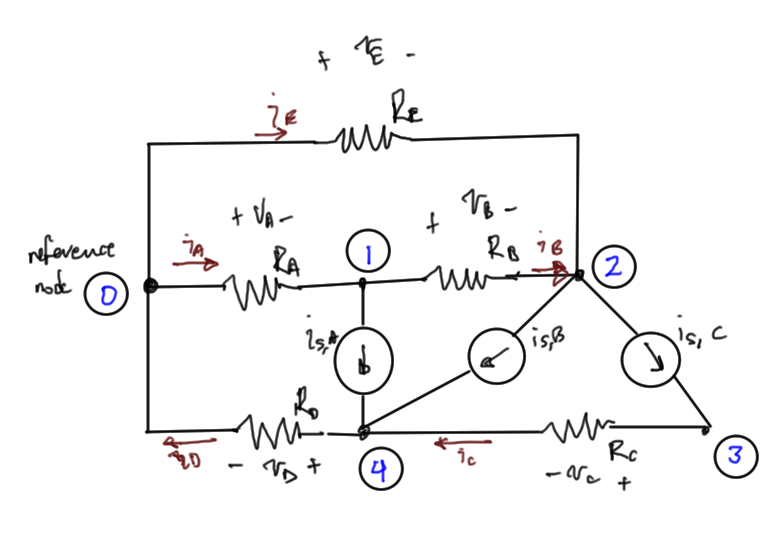
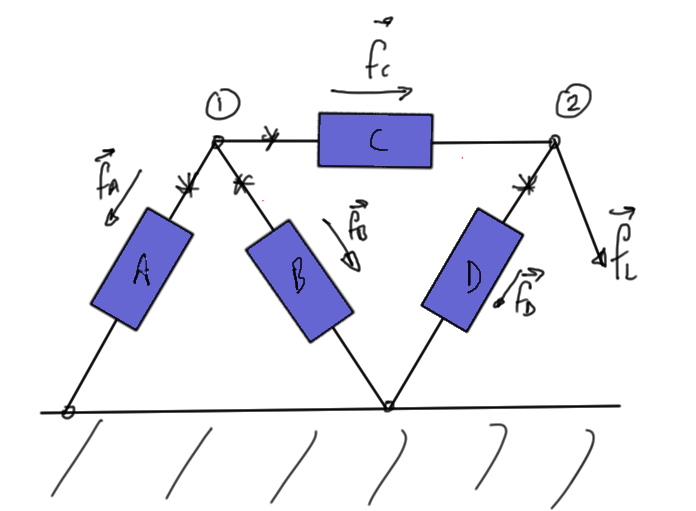
Consider the sample circuit of fig. 1.

fig. 1. Sample resistive circuit

fig. 1. Sample resistive circuit

Step 1. Choose unknowns:

For this problem, let’s take

  • node voltages: \(V_1, V_2, V_3, V_4\)

  • branch currents: \(i_A, i_B, i_C, i_D, i_E\)

We do not need to introduce additional labels for the source current sources.
We always introduce a reference node and call that zero.

For a circuit with \(N\) nodes, and \(B\) resistors, there will be \(N-1\) unknown node voltages and \(B\) unknown branch currents, for a total number of \(N – 1 + B\) unknowns.

Step 2. Conservation equations:

KCL

  • 0: \(i_A + i_E – i_D = 0\)
  • 1: \(-i_A + i_B + i_{S,A} = 0\)
  • 2: \(-i_B + i_{S,B} – i_E + i_{S,C} = 0\)
  • 3: \(i_C – i_{S,C} = 0\)
  • 4: \(-i_{S,A} – i_{S,B} + i_D – i_C = 0\)

Grouping unknown currents, this is

  • 0: \(i_A + i_E – i_D = 0\)
  • 1: \(-i_A + i_B = -i_{S,A}\)
  • 2: \(-i_B -i_E = -i_{S,B} -i_{S,C}\)
  • 3: \(i_C = i_{S,C}\)
  • 4: \(i_D – i_C = i_{S,A} + i_{S,B}\)

Note that one of these equations is redundant (sum 1-4). In a circuit with \(N\) nodes, we can write at most \(N-1\) independent KCLs.

In matrix form

\begin{equation}\label{eqn:multiphysicsL2:20}
\begin{bmatrix}
-1 & 1 & 0 & 0 & 0 \\
0 & -1 & 0 & 0 & -1 \\
0 & 0 & 1 & 0 & 0 \\
0 & 0 & -1 & 1 & 0
\end{bmatrix}
\begin{bmatrix}
i_A \\
i_B \\
i_C \\
i_D \\
i_E \\
\end{bmatrix}
=
\begin{bmatrix}
-i_{S,A} \\
-i_{S,B} -i_{S,C} \\
i_{S,C} \\
i_{S,A} + i_{S,B}
\end{bmatrix}
\end{equation}

We call this first matrix of ones and minus ones the incidence matrix \(A\). This matrix has \(B\) columns and \(N-1\) rows. We call the known current matrix \(\overline{I}_S\), and the branch currents \(\overline{I}_B\). That is

\begin{equation}\label{eqn:multiphysicsL2:40}
A \overline{I}_B = \overline{I}_S.
\end{equation}

Observe that we have both a plus and minus one in all columns except for those columns impacted by our neglect of the reference node current conservation equation.

Algorithm for filling \(A\)

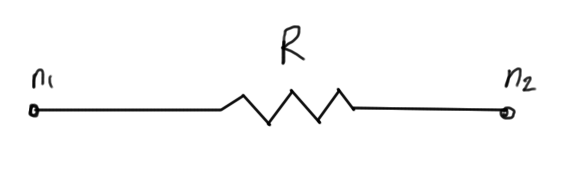
In the input file, to describe a resistor of fig. 2, you’ll have a line of the form

R name \(n_1\) \(n_2\) value

fig. 2. Resistor node convention

fig. 2. Resistor node convention

The algorithm to process resistor lines is

\begin{equation*}
\begin{aligned}
&A \leftarrow 0 \\
&ic \leftarrow 0 \\
&\text{forall resistor lines} \\
&ic \leftarrow ic + 1, \text{adding one column to \(A\)} \\
&\text{if}\ n_1 != 0 \\
&A(n_1, ic) \leftarrow +1 \\
&\text{endif} \\
&\text{if}\ n_2 != 0 \\
&A(n_2, ic) \leftarrow -1 \\
&\text{endif} \\
&\text{endfor} \\
\end{aligned}
\end{equation*}

Algorithm for filling \(\overline{I}_S\)

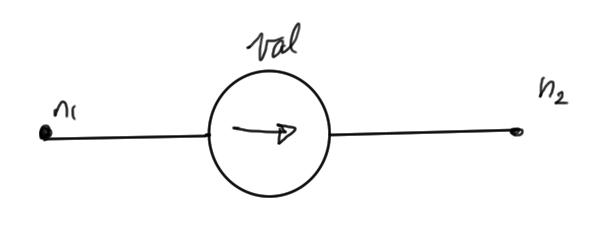
Current sources, as in fig. 3, a line will have the specification (FIXME: confirm… didn’t write this down).

I name \(n_1\) \(n_2\) value

fig. 3. Current source conventions

fig. 3. Current source conventions

\begin{equation*}
\begin{aligned}
&\overline{I}_S = \text{zeros}(N-1, 1) \\
&\text{forall current lines} \\
&\overline{I}_S(n_1) \leftarrow \overline{I}_S(n_1) – \text{value} \\
&\overline{I}_S(n_2) \leftarrow \overline{I}_S(n_1) + \text{value} \\
&\text{endfor}
\end{aligned}
\end{equation*}

Step 3. Constitutive equations:

\begin{equation}\label{eqn:multiphysicsL2:60}
\begin{bmatrix}
i_A \\
i_B \\
i_C \\
i_D \\
i_E
\end{bmatrix}
=
\begin{bmatrix}
1/R_A & & & & \\
& 1/R_B & & & & \\
& & 1/R_C & & & \\
& & & 1/R_D & & \\
& & & & & 1/R_E
\end{bmatrix}
\begin{bmatrix}
v_A \\
v_B \\
v_C \\
v_D \\
v_E
\end{bmatrix}
\end{equation}

Or

\begin{equation}\label{eqn:multiphysicsL2:80}
\overline{I}_B = \alpha \overline{V}_B,
\end{equation}

where \(\overline{V}_B\) are the branch voltages, not unknowns of interest directly. We can write

\begin{equation}\label{eqn:multiphysicsL2:100}
\begin{bmatrix}
v_A \\
v_B \\
v_C \\
v_D \\
v_E
\end{bmatrix}
=
\begin{bmatrix}
-1 & & & \\
1 & -1 & & \\
& & 1 & -1 \\
& & & 1 \\
& -1 & &
\end{bmatrix}
\begin{bmatrix}
v_1 \\
v_2 \\
v_3 \\
v_4
\end{bmatrix}
\end{equation}

Observe that this is the transpose of \(A\), allowing us to write

\begin{equation}\label{eqn:multiphysicsL2:120}
\overline{V}_B = A^\T \overline{V}_N.
\end{equation}

Solving

  • KCLs: \(A \overline{I}_B = \overline{I}_S\)

  • constitutive: \(\overline{I}_B = \alpha \overline{V}_B \Rightarrow \overline{I}_B = \alpha A^\T \overline{V}_N\)

  • branch and node voltages: \(\overline{V}_B = A^\T \overline{V}_N\)

In block matrix form, this is

\begin{equation}\label{eqn:multiphysicsL2:140}
\begin{bmatrix}
A & 0 \\
I & -\alpha A^\T
\end{bmatrix}
\begin{bmatrix}
\overline{I}_B \\
\overline{V}_N
\end{bmatrix}
=
\begin{bmatrix}
\overline{I}_S \\
0
\end{bmatrix}.
\end{equation}

Is it square? We see that it is after observing that we have

  • \(N-1\) rows in \(A\) , and \(B\) columns.
  • \(B\) rows in \(I\).
  • \(N-1\) columns.

ECE1254H Modeling of Multiphysics Systems. Lecture 1: Analogies to circuit systems. Taught by Prof. Piero Triverio

September 22, 2014 ece1254

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. May not be entirely coherent.

In slides

A review of systematic nodal analysis for a basic resistive circuit was outlined in slides, with a subsequent attempt to show how many similar linear systems can be modeled as circuits so that the same toolbox can be applied. This included blood flow through a body (and blood flow to the brain), a model of antenna interference in a portable phone, heat conduction in a one dimensional conductor under a heat lamp, and a few other systems.

This discussion reminded me of the joke where the farmer, the butcher and the physicist are all invited to talk at a beef convention. After meaningful and appropriate talks by the farmer and the butcher, the physicist gets his chance, and proceeds with “We begin by modeling the cow as a sphere, …”. The ECE equivalent of that appears to be a Kirchhoff circuit problem.

Mechanical structures example

Continuing the application of circuits like linear systems to other systems, let’s consider a truss system as illustrated in fig. 1, or in the simpler similar system of fig. 2.

fig. 1. A static loaded truss configuratio

fig. 1. A static loaded truss configuratio

fig 2. Simple static load

fig 2. Simple static load

Our unknowns are

  • positions of the joints after deformation \((x_i, y_i)\).
  • force acting on each strut \(\BF_j = (F_{j,x}, F_{j,y})\).

The constitutive equations, assuming static conditions (steady state, no transients)

  • Load force. \(\BF_L = (F_{L, x}, F_{L, y}) = (0, -m g)\).
  • Strut forces. Under static conditions the total resulting force on the strut is zero, so \(\BF’_j = -\BF_j\). For this problem it is redundant to label forces on both ends, so we mark the labeled end of the object with an asterisk as in fig. 3.
fig 3. Strut model

fig 3. Strut model

Consider a simple case

One strut as in fig. 4.

fig. 4. Very simple static load

fig. 4. Very simple static load

\begin{equation}\label{eqn:multiphysicsL1:20}
\BF^\conj = – \Ba_x
\underbrace{
\epsilon
}_{\text{constant, describes the beam elasticity, given}}
\biglr{
\underbrace{
L
}_{\text{unloaded length \(L = \Abs{x^\conj – 0}\), given}}
– L_0}
\end{equation}

The constitutive law for a general strut as in fig. 5 is

fig 5. Strut force diagram

fig 5. Strut force diagram

The force is directed along the unit vector

\begin{equation}\label{eqn:multiphysicsL1:40}
\Be = \frac{\Br^\conj – \Br}{\Abs{\Br^\conj – \Br}},
\end{equation}

and has the form
\begin{equation}\label{eqn:multiphysicsL1:60}
\BF^\conj = – \Be \epsilon \lr{ L – L_0 }.
\end{equation}

The value \(\epsilon\) may be related to Hooks’ constant, and \(L_0\) is given by

\begin{equation}\label{eqn:multiphysicsL1:80}
L = \Abs{\Br^\conj – \Br} = \sqrt{(x^\conj – x)^2 + (y^\conj – y)^2}.
\end{equation}

Observe that the relation between \(\BF^\conj\) and position is nonlinear!

Treatment of this system will be used as the prototype for our handling of other nonlinear systems.

Returning to the simple static system, and introducing force and joint labels as in fig. 6, we can examine the \textAndIndex{conservation law}, the balance of forces.

fig 6. Strut system

fig 6. Strut system

  • At joint 1:\begin{equation}\label{eqn:multiphysicsL1:100}
    \Bf_A + \Bf_B + \Bf_C = 0
    \end{equation}or
    \begin{equation}\label{eqn:multiphysicsL1:120}
    \begin{aligned}
    \Bf_{A,x} + \Bf_{B,x} + \Bf_{C,x} &= 0 \\
    \Bf_{A,y} + \Bf_{B,y} + \Bf_{C,y} &= 0
    \end{aligned}
    \end{equation}
  • At joint 2:\begin{equation}\label{eqn:multiphysicsL1:140}
    -\Bf_C + \Bf_D + \Bf_L = 0
    \end{equation}or
    \begin{equation}\label{eqn:multiphysicsL1:160}
    \begin{aligned}
    -\Bf_{C,x} + \Bf_{D,x} + \Bf_{L,x} &= 0 \\
    -\Bf_{C,y} + \Bf_{D,y} + \Bf_{L,y} &= 0
    \end{aligned}
    \end{equation}

We have an equivalence

  • Force \(\leftrightarrow\) Current.
  • Force balance equation \(\leftrightarrow\) KCL

Sundried tomatoes in oil and vinegar

September 15, 2014 Food , , ,

 

The grocery stores sell little bottles of sundried tomatoes, packed in oil and vinegar.  These are tasty, good in salads, sandwiches, wraps and many other things, but at $3-$5, you don’t get very much for the money.

You can also buy whole or halved sundried tomatoes in bigger packages.  For $10 I can get a sizeable shrink wrapped bag of these at the local grocery store, which can then be cut into slivers

 

photo 1

Place these into an empty washed jar,

photo 2 add some oil and vinegar photo 3

a bit of salt, and then shake vigorously, resulting in a slimy looking mix

 

photo 5

 

Let this sit for a day or so in the fridge, and it will be ready to eat (it will also loose the slimy look that occurs just after shaking).

You’ll get a large number of batches out of the bulk sundried tomatoes this way, with not very much cost in time to prepare.

Enjoy your salad, sandwich, spaghetti, or many other things that are good with this nice topping.

A debugger walk through an out of module call on AIX

August 29, 2014 C/C++ development and debugging. , , , , , ,

We were seeing the following powerpc instruction sequence mess up, ending up
with the CTR (counter) register containing zero. The CTR register, which can
be used for computed gotos and other stuff, is one of the only registers that I believe can be
both loaded and branched to easily on powerpc, and is one of the volatile
regisers in the ABI (one that doesn’t have to be spilled to and from the stack
before another call).

0x090000000A9E8B78 : E8040000 ld r0,0(r4)
0x090000000A9E8B7C : 7C0903A6 mtctr r0
0x090000000A9E8B80 : E8440008 ld r2,8(r4)
0x090000000A9E8B84 : 4E800421 bctrl # 20,bit0

I had a recollection that this sequence was a call through a function pointer,
but thought it may also be what we get for a plain old out of module call
(calling something in a shared library from the main text segment or a call to some other shared
library function from a shared library function). Let’s see what an out of module looks like, for a simple call like

#include <stdio.h>

int main(int argc, char ** argv)
{
   printf( "out of module call\n" ) ;

   return 0;
}

I set an instruction breakpoint at the bl (branch and link) instruction for
printf, and then step into that

(dbx) stopi at 0x100000788
[1] stopi at 0x100000788 (main+0x28)
(dbx) c
[1] stopped in main at 0x100000788
0x100000788 (main+0x28) 48000059 bl 0x1000007e0 (printf)
(dbx) stepi
stopped in glink64.printf at 0x1000007e0
0x1000007e0 (printf) e98200d8 ld r12,0xd8(r2)
(dbx)

Observe that the debugger is letting us know that we aren’t actually in printf
yet, but are in the glue code for printf. Looking at the instruction sequence
for this glue code we see that it matches the type of code we saw in out NULL
CTR trap sequence above

stopped in glink64.printf at 0x1000007e4
0x1000007e4 (printf+0x4) f8410028 std r2,0x28(r1)
(dbx)

stopped in glink64.printf at 0x1000007e8
0x1000007e8 (printf+0x8) e80c0000 ld r0,0x0(r12)
(dbx)

stopped in glink64.printf at 0x1000007ec
0x1000007ec (printf+0xc) e84c0008 ld r2,0x8(r12)
(dbx)

stopped in glink64.printf at 0x1000007f0
0x1000007f0 (printf+0x10) 7c0903a6 mtctr r0

We save our TOC register (GR2, the table of contents register) to the stack,
load a new value into GR0 to copy to the CTR register, and load the TOC
register (GR2) for the module that we are calling.

Now if we look at what just got put in the TOC register, we see that it’s the
address that we find the actual code for printf at

(dbx) p $r0
0x0900000000004f80
(dbx) listi 0x0900000000004f80
0x900000000004f80 (printf) fbe1fff8 std r31,-8(r1)
0x900000000004f84 (printf+0x4) fbc1fff0 std r30,-16(r1)
0x900000000004f88 (printf+0x8) 7c0802a6 mflr r0
0x900000000004f8c (printf+0xc) fba1ffe8 std r29,-24(r1)
0x900000000004f90 (printf+0x10) ebe20dd0 ld r31,0xdd0(r2)
0x900000000004f94 (printf+0x14) f8010010 std r0,0x10(r1)
0x900000000004f98 (printf+0x18) 8002000c lwz r0,0xc(r2)
0x900000000004f9c (printf+0x1c) f821ff71 stdu r1,-144(r1)
0x900000000004fa0 (printf+0x20) 60000000 ori r0,r0,0x0
0x900000000004fa4 (printf+0x24) 2c000000 cmpi cr0,0x0,r0,0x0

The glue code, a branch table for out of module calls, gets us to there, but
we have to pay a number of instruction penalty for this call, in addition to
the normal function call overhead.

What does this mean for the trap scenerio? One implication is that this isn’t
neccessarily as simple as a NULL function pointer. That instruction sequence
is probably different (but I don’t recall exactly how at the moment). Perhaps
this means that the jump table for the currently exectuting shared library got
corrupted? It is probably writable since the run time loader must be able to
modify it. I’d guess that it remains writable throughout execution to support
lazy runtime loader address fixups. This is likely not going to be an easy
problem to solve.

Apple Bonjour service shutting down my computer?

August 7, 2014 Incoherent ramblings , , ,

 

I’ve been running the armory bitcoin client, which has a very cpu and network intensive initial setup.  Two days in a row I attempted to let it run overnight, only to find my computer shutdown in the morning (with errors about improper shutdown on boot).

In both cases, the very last thing that I see in my system event log are timeouts for the Bonjour service.  Last night, the last stuff in the log before shutdown was:

Capture

and the night before:

Capture

I’m wondering if anybody else has seen similar unexpected shutdown occur.  I’m wondering if Bonjour is raising some sort of abort that manages to shutdown my system?