The lldb TUI (text user interface)

August 26, 2019 C/C++ development and debugging. , , ,

It turns out, like GDB, that lldb has a TUI mode too, but it’s really simplistic.  You enter with

(lldb) gui

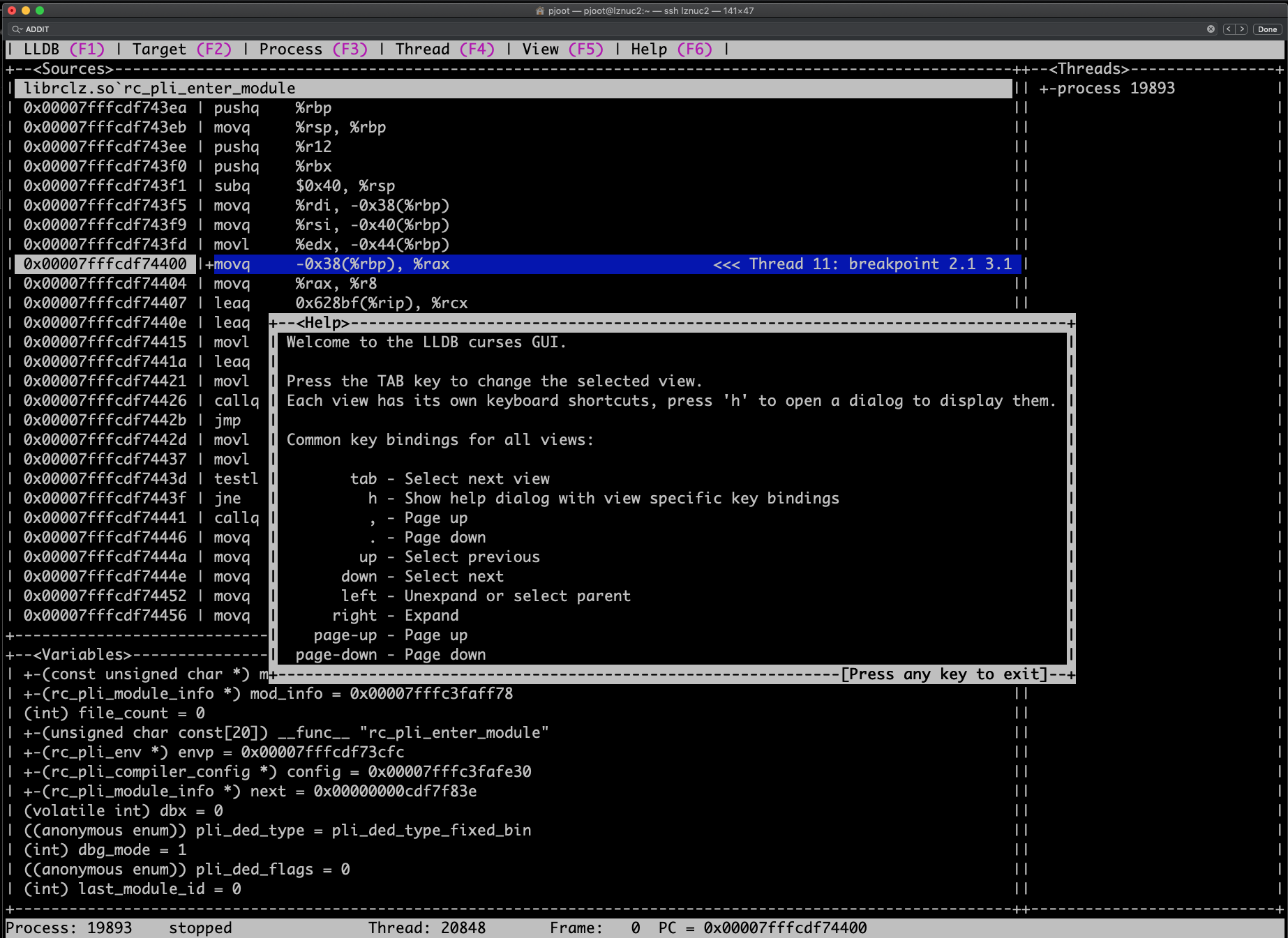
at which point you get a full screen of code or assembly, and options for register exploration, thread and stack exploration, and a variable view.  The startup screen looks like:

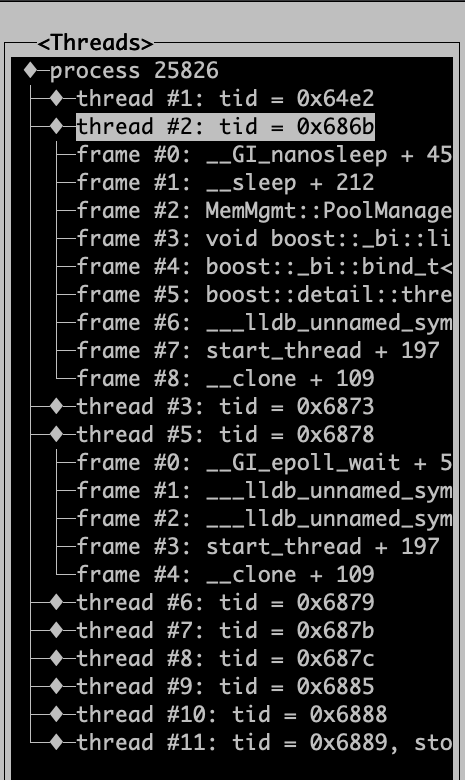
If you tab over to the Threads window, you can space select the process, and drill into the stack traces for any of the running threads

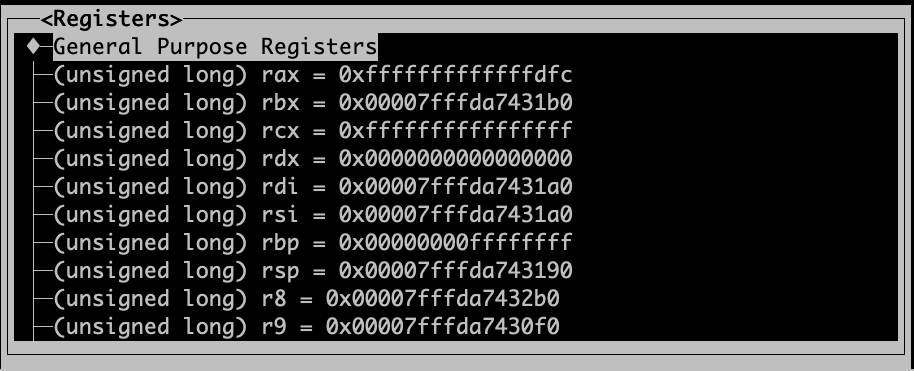
You can also expand the regsiters by register class:

I’d like to know how to resize the various windows.  If you resize the terminal, the size of the stack view pane seems to remain fixed, so the symbol names always end up truncated.

Apparently this code hasn’t been maintained or developed since it was added.  Because there is no console pane, you have to set all desired breakpoints and continue, then pop into the GUI to look at stuff, and then <F1> to get back to the console prompt.  It’s nice that it gives you a larger view of the code, but given that lldb already displays context around each line, the lldb TUI isn’t that much of a value add in that respect.

This “GUI” would actually be fairly usable if it just had a console pane.

My youngest reader

August 23, 2019 Incoherent ramblings ,

My nephew Jake is a prodigy, and is already tackling QM!

Two more books dispatched: Art of the Deal, and Deception Point.

August 3, 2019 Incoherent ramblings, Reviews , , , ,

I’ve been working hard to take down my backlog of books to read, and have now finished two more.

1) Trump’s: The Art of the Deal.

Other possible alternate titles for this book would be “How I financed my projects at others’ expense using  tax rebates and other tricks”, and “How I used PR to get what I want.”  Reading this leaves you with the slightly nauseous feeling that you have after talking to a slimy used car salesman.  A lot of what was stated left me with the feeling that relevant facts were being omitted.  I’d like to see a fact checking “Coles Notes” for this book, and to look at how the projects that are named in the book are doing now.

I am inclined to enumerate all the people that Trump mentions in the book and dig into the relationships that Trump took the time to name drop in this book.  Trump’s pedophile buddy Epstein didn’t make the cut in the book, but Adnan Khashoggi did. A lot of the other names I didn’t recognize.

EDIT: here’s some backstory on the book.  Included in that article was one more interesting name drop, Roy Cohn, Trump’s lawyer.  That name may have been mentioned in the book, but if so, I didn’t recognize it when I read that part of the book.  With Epstein’s case reactivated, I now recognize Cohn’s name from Whitney Webb’s writing [1], [2] and her interview with Pierce Redmond.

2) Dan Brown’s: Deception point.

This book would be a lot better as a movie. Like a lot of Michael Crichton books, this one moves very fast, but is pretty shallow, as well as predictable and probably forgettable.  I did enjoy it, but it’s definitely not one to keep, and I intend to bring it to the second hand bookstore, or if they don’t want it, to the communal take-or-leave a book shelf at the recycling depot.

References

[1] Hidden in Plain Sight: The Shocking Origins of the Jeffrey Epstein Case

[2] Government by Blackmail: Jeffrey Epstein, Trump’s Mentor and the Dark Secrets of the Reagan Era

Gatto’s “Dumbing Us Down”

July 20, 2019 Incoherent ramblings , , ,

 

I’ve just read John Taylor Gatto’s “Dumbing Us Down, the hidden curriculum of compulsory schooling.”  I’ve heard Brett Veinotte on the School Sucks Podcast talk about Gatto’s exposition of the origins of the North American school system.  Given that, I expected a lot more from this particular book.  Instead this book is a largely a collection of speeches, converted into essay form, as opposed to a systematic deconstruction of the school system.

I did enjoy those essays, but my reaction included a lot of “Sir, you are preaching to the choir.”  I am guessing that the book that I really wanted was his “The Underground History of American Education“, which weighs in at ~450 pages.

A interesting video with some analysis of the Wim Hof method

July 14, 2019 Incoherent ramblings , , ,

I’d heard the Wim Hof interview on Joe Rogan a while ago (youtube link no longer available), which was pretty interesting.

Due to the indoctrination of my youth(*), I recognize that I’m predisposed to the idea that the mind can control the body, so the techniques that Wof described in the Rogan podcast seemed plausible.  However, that plausibility wasn’t enough to make me want to spend the money me to purchase his book.

I have to admit that I did try some Wim Hof style intense breathing before jumping in the late fall 50F pool, after some time in the hot tub.  I suspect that I was not doing the breathing exercises correctly.  At that pool temperature, without the ablity to self-regulate my body heat, I find that I don’t warm up, even after a number of laps.

For anybody that finds the idea of body self regulation interesting, here is some analysis of the Wim Hof method on the medlife youtube channel.  It may not be the way to acquire Bene Gesserit like abilities, however,  if you also have the urge to play the hot-tub/cold-pool alternation game, or climb mountains, it does sound like the breathing techniques are worth knowing.

Footnotes:

(*) I grew up Scientology household where the actor at the head of the body-mind-spirit story is an all-powerful entity, somewhat akin to a Jin, but in need of significant re-training.