DISCLAIMER: Very rough notes from class, with some additional side notes.
These are notes for the UofT course PHY2403H, Quantum Field Theory I, taught by Prof. Erich Poppitz fall 2018.
Last time
We followed a sequence of operations
- Noether’s theorem
- \( \rightarrow \) conserved currents
- \( \rightarrow \) charges (classical)
- \( \rightarrow \) “correspondence principle”
- \( \rightarrow \hatQ \)
- Hermitian operators
- “generators of symmetry”
\begin{equation}\label{eqn:qftLecture9:20}
\hatU(\alpha) = e^{i \alpha \hatQ}
\end{equation}
We found
\begin{equation}\label{eqn:qftLecture9:40}
\hatU(\alpha) \phihat \hatU^\dagger(\alpha) = \phihat + i \alpha \antisymmetric{\hatQ}{\phihat} + \cdots
\end{equation}
Example: internal symmetries:
(non-spacetime), such as \( O(N)\) or \( U(1) \).
In QFT internal symmetries can have different “\underline{modes of realization}”.
- [I]
- “Wigner mode”. These are also called “unbroken symmetries”.
\begin{equation}\label{eqn:qftLecture9:60}
\hatQ \ket{0} = 0
\end{equation}
i.e. \( \hatU(\alpha) \ket{0} = 0 \).
Ground state invariant. Formally \( :\hatQ: \) annihilates \( \ket{0} \).
\( \antisymmetric{\hatQ}{\hatH} = 0 \) implies that all eigenstates are eigenstates of \( \hatQ \) in \( U(1) \). Example from HW 1
\begin{equation}\label{eqn:qftLecture9:80}
\hatQ = \text{“charge” under \( U(1) \)}.
\end{equation}
All states have definite charge, just live in QU. - “Nambu-Goldstone mode” (Landau-ginsburg). This is also called a “spontaneously broken symmetry”\footnote{
First encounter example (HWII, \( SU(2) \times SU(2) \rightarrow SU(2) \)). Here a \( U(1) \) spontaneous broken symmetry.}.
\( H \) or \( L \) is invariant under symmetry, but ground state is not.
Example:
\begin{equation}\label{eqn:qftLecture9:100}
\LL = \partial_\mu \phi^\conj \partial^\mu \phi – V(\Abs{\phi}),
\end{equation}
where
\begin{equation}\label{eqn:qftLecture9:120}
V(\Abs{\phi}) = m^2 \phi^\conj \phi + \frac{\lambda}{4} \lr{ \phi^\conj \phi }^2.
\end{equation}
When \( m^2 > 0 \) we have a Wigner mode, but when \( m^2 < 0 \) we have an issue: \( \phi = 0 \) is not a minimum of potential.
When \( m^2 < 0 \) we write
\begin{equation}\label{eqn:qftLecture9:140}
\begin{aligned}
V(\phi)
&= – m^2 \phi^\conj \phi + \frac{\lambda}{4} \lr{ \phi^\conj \phi}^2 \\
&= \frac{\lambda}{4} \lr{
\lr{ \phi^\conj \phi}^2 – \frac{4}{\lambda} m^2 } \\
&= \frac{\lambda}{4} \lr{
\phi^\conj \phi – \frac{2}{\lambda} m^2 }^2 – \frac{4 m^4}{\lambda^2},
\end{aligned}
\end{equation}
or simply
\begin{equation}\label{eqn:qftLecture9:780}
V(\phi)
=
\frac{\lambda}{4} \lr{ \phi^\conj \phi – v^2 }^2 + \text{const}.
\end{equation}
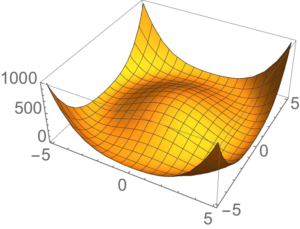
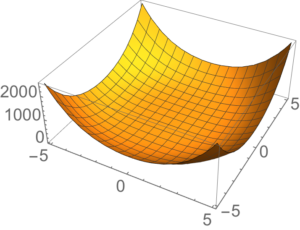
The potential (called the Mexican hat potential) is illustrated in fig. 1 for non-zero \( v \), and in
fig. 2 for \( v = 0 \).
We choose to expand around some point on the minimum ring (it doesn’t matter which one).
When there is no potential, we call the field massless (i.e. if we are in the minimum ring).
We expand as
\begin{equation}\label{eqn:qftLecture9:160}
\phi(x) = v \lr{ 1 + \frac{\rho(x)}{v} } e^{i \alpha(x)/v },
\end{equation}
so
\begin{equation}\label{eqn:qftLecture9:180}
\begin{aligned}
\frac{\lambda}{4}
\lr{\phi^\conj \phi – v^2}^2
&=
\lr{
v^2 \lr{ 1 + \frac{\rho(x)}{v} }^2
– v^2
}^2 \\
&=
\frac{\lambda}{4}
v^4 \lr{ \lr{ 1 + \frac{\rho(x)}{v} }^2 – 1 } \\
&=
\frac{\lambda}{4}
v^4
\lr{
\frac{2 \rho}{v} + \frac{\rho^2}{v^2}
}^2.
\end{aligned}
\end{equation}
\begin{equation}\label{eqn:qftLecture9:200}
\partial_\mu \phi =
\lr{
v \lr{ 1 + \frac{\rho(x)}{v} } \frac{i}{v} \partial_\mu \alpha
+ \partial_\mu \rho
} e^{i \alpha}
\end{equation}
so
\begin{equation}\label{eqn:qftLecture9:220}
\begin{aligned}
\LL
&= \Abs{\partial \phi^\conj}^2 – \frac{\lambda}{4} \lr{ \Abs{\phi^\conj}^2 – v^2 }^2 \\
&=
\partial_\mu \rho \partial^\mu \rho + \partial_\mu \alpha \partial^\mu \alpha \lr{ 1 + \frac{\rho}{v} }
–
\frac{\lambda v^4}{4} \frac{ 4\rho^2}{v^2} + O(\rho^3) \\
&=
\partial_\mu \rho \partial^\mu \rho
– \lambda v^2\rho^2
+
\partial_\mu \alpha \partial^\mu \alpha \lr{ 1 + \frac{\rho}{v} }.
\end{aligned}
\end{equation}
We have two fields, \( \rho \) : a massive scalar field, the “Higgs”, and a massless field \( \alpha \) (the Goldstone Boson).
\( U(1) \) symmetry acts on \( \phi(x) \rightarrow e^{i \omega } \phi(x) \) i.t.o \( \alpha(x) \rightarrow \alpha(x) + v \omega \).
\( U(1) \) global symmetry (broken) acts on the Goldstone field \( \alpha(x) \) by a constant shift. (\(U(1)\) is still a symmetry of the Lagrangian.)
The current of the \( U(1) \) symmetry is:
\begin{equation}\label{eqn:qftLecture9:240}
j_\mu = \partial_\mu \alpha \lr{ 1 + \text{higher dimensional \( \rho \) terms} }.
\end{equation}
When we quantize
\begin{equation}\label{eqn:qftLecture9:260}
\alpha(x) =
\int \frac{d^3p}{(2\pi)^3 \sqrt{ 2 \omega_p }} e^{i \omega_p t – i \Bp \cdot \Bx} \hat{a}_\Bp^\dagger +
\int \frac{d^3p}{(2\pi)^3 \sqrt{ 2 \omega_p }} e^{-i \omega_p t + i \Bp \cdot \Bx} \hat{a}_\Bp
\end{equation}
\begin{equation}\label{eqn:qftLecture9:280}
j^\mu(x) = \partial^\mu \alpha(x) =
\int \frac{d^3p}{(2\pi)^3 \sqrt{ 2 \omega_p }} \lr{ i \omega_\Bp – i \Bp } e^{i \omega_p t – i \Bp \cdot \Bx} \hat{a}_\Bp^\dagger +
\int \frac{d^3p}{(2\pi)^3 \sqrt{ 2 \omega_p }} \lr{ -i \omega_\Bp + i \Bp } e^{-i \omega_p t + i \Bp \cdot \Bx} \hat{a}_\Bp.
\end{equation}
\begin{equation}\label{eqn:qftLecture9:300}
j^\mu(x) \ket{0} \ne 0,
\end{equation}
instead it creates a single particle state.
Examples of symmetries
In particle physics, examples of Wigner vs Nambu-Goldstone, ignoring gravity the only exact internal symmetry in the standard module is
\( (B\# – L\#) \), believed to be a \( U(1) \) symmetry in Wigner mode.
Here \(B\#\) is the Baryon number, and \( L\# \) is the Lepton number. Examples:
- \( B(p) = 1 \), proton.
- \( B(q) = 1/3 \), quark
- \( B(e) = 1 \), electron
- \( B(n) = 1 \), neutron.
- \( L(p) = 1 \), proton.
- \( L(q) = 0 \), quark.
- \( L(e) = 0 \), electron.
The major use of global internal symmetries in the standard model is as “approximate” ones. They become symmetries when one neglects some effect( “terms in \( \LL \)”).
There are other approximate symmetries (use of group theory to find the Balmer series).
Example from HW2:
QCD in limit
\begin{equation}\label{eqn:qftLecture9:320}
m_u = m_d = 0.
\end{equation}
\( m_u m_d \ll m_p \) (the products of the up-quark mass and the down-quark mass are much less than a composite one (name?)).
\( SU(2)_L \times SU(2)_R \rightarrow SU(2)_V \)
EWSB (Electro-Weak-Symmetry-Breaking) sector
When the couplings \( g_2, g_1 = 0 \). (\( g_2 \in SU(2), g_1 \in U(1) \)).
Scale invariance
\begin{equation}\label{eqn:qftLecture9:340}
\begin{aligned}
x &\rightarrow e^{\lambda} x \\
\phi &\rightarrow e^{-\lambda} \phi \\
A_\mu &\rightarrow e^{-\lambda} A_\mu
\end{aligned}
\end{equation}
Any unitary theory which is scale invariant is also \underline{conformal} invariant. Conformal invariance means that angles are preserved.
The point here is that there is more than scale invariance.
We have classical internal global continuous symmetries.
These can be either
- “unbroken” (Wigner mode)
\begin{equation}\label{eqn:qftLecture9:360}
\hatQ\ket{0} = 0.
\end{equation} - “spontaneously broken”
\begin{equation}\label{eqn:qftLecture9:380}
j^\mu(x) \ket{0} \ne 0
\end{equation}
(creates Goldstone modes). - “anomalous”. Classical symmetries are not a symmetry of QFT.
Examples:- Scale symmetry (to be studied in QFT II), although this is not truly internal.
- In QCD again when \( \omega_\Bq = 0 \), a \( U(1\) symmetry (chiral symmetry) becomes exact, and cannot be preserved in QFT.
- In the standard model (E.W sector), the Baryon number and Lepton numbers are not symmetries, but their difference \( B\# – L\# \) is a symmetry.
Lorentz invariance.
We’d like to study the action of Lorentz symmetries on quantum states. We are going to “go by the book”, finding symmetries, currents, quantize, find generators, and so forth.
Under a Lorentz transformation
\begin{equation}\label{eqn:qftLecture9:400}
x^\mu \rightarrow {x’}^\mu = {\Lambda^\mu}_\nu x^\nu,
\end{equation}
We are going to consider infinitesimal Lorentz transformations
\begin{equation}\label{eqn:qftLecture9:420}
{\Lambda^\mu}_\nu \approx
{\delta^\mu}_\nu + {\omega^\mu}_\nu
,
\end{equation}
where \( {\omega^\mu}_\nu \) is small.
A Lorentz transformation \( \Lambda \) must satisfy \( \Lambda^\T G \Lambda = G \), or
\begin{equation}\label{eqn:qftLecture9:800}
g_{\mu\nu} = {{\Lambda}^\alpha}_\mu g_{\alpha \beta} {{\Lambda}^\beta}_\nu,
\end{equation}
into which we insert the infinitesimal transformation representation
\begin{equation}\label{eqn:qftLecture9:820}
\begin{aligned}
0
&=
– g_{\mu\nu} +
\lr{ {\delta^\alpha}_\mu + {\omega^\alpha}_\mu }
g_{\alpha \beta}
\lr{ {\delta^\beta}_\nu + {\omega^\beta}_\nu } \\
&=
– g_{\mu\nu} +
\lr{
g_{\mu \beta}
+
\omega_{\beta\mu}
}
\lr{ {\delta^\beta}_\nu + {\omega^\beta}_\nu } \\
&=
– g_{\mu\nu} +
g_{\mu \nu}
+
\omega_{\nu\mu}
+
\omega_{\mu\nu}
+
\omega_{\beta\mu}
{\omega^\beta}_\nu.
\end{aligned}
\end{equation}
The quadratic term can be ignored, leaving just
\begin{equation}\label{eqn:qftLecture9:840}
0 =
\omega_{\nu\mu}
+
\omega_{\mu\nu},
\end{equation}
or
\begin{equation}\label{eqn:qftLecture9:860}
\omega_{\nu\mu} = – \omega_{\mu\nu}.
\end{equation}
Note that \( \omega \) is a completely antisymmetric tensor, and like \( F_{\mu\nu} \) this has only 6 elements.
This means that the
infinitesimal transformation of the coordinates is
\begin{equation}\label{eqn:qftLecture9:440}
x^\mu \rightarrow {x’}^\mu \approx x^\mu + \omega^{\mu\nu} x_\nu,
\end{equation}
the field transforms as
\begin{equation}\label{eqn:qftLecture9:460}
\phi(x) \rightarrow \phi'(x’) = \phi(x)
\end{equation}
or
\begin{equation}\label{eqn:qftLecture9:760}
\phi'(x^\mu + \omega^{\mu\nu} x_\nu) =
\phi'(x) + \omega^{\mu\nu} x_\nu \partial_\mu\phi(x) = \phi(x),
\end{equation}
so
\begin{equation}\label{eqn:qftLecture9:480}
\delta \phi = \phi'(x) – \phi(x) =
-\omega^{\mu\nu} x_\nu \partial_\mu \phi.
\end{equation}
Since \( \LL \) is a scalar
\begin{equation}\label{eqn:qftLecture9:500}
\begin{aligned}
\delta \LL
&=
-\omega^{\mu\nu} x_\nu \partial_\mu \LL \\
&=
–
\partial_\mu \lr{
\omega^{\mu\nu} x_\nu \LL
}
+
(\partial_\mu x_\nu) \omega^{\mu\nu} \LL \\
&=
\partial_\mu \lr{
–
\omega^{\mu\nu} x_\nu \LL
},
\end{aligned}
\end{equation}
since \( \partial_\nu x_\mu = g_{\nu\mu} \) is symmetric, and \( \omega \) is antisymmetric.
Our current is
\begin{equation}\label{eqn:qftLecture9:520}
J^\mu_\omega
=
–
\omega^{\mu\nu} x_\mu \LL
.
\end{equation}
Our Noether current is
\begin{equation}\label{eqn:qftLecture9:540}
\begin{aligned}
j^\nu_{\omega^{\mu\rho}}
&= \PD{\phi_{,\nu}}{\LL} \delta \phi – J^\mu_\omega \\
&=
\partial^\nu \phi\lr{ – \omega^{\mu\rho} x_\rho \partial_\mu \phi } + \omega^{\nu \rho} x_\rho \LL \\
&=
\omega^{\mu\rho}
\lr{
\partial^\nu \phi\lr{ – x_\rho \partial_\mu \phi } + {\delta^{\nu}}_\mu x_\rho \LL
} \\
&=
\omega^{\mu\rho} x_\rho
\lr{
-\partial^\nu \phi \partial_\mu \phi + {\delta^{\nu}}_\mu \LL
}
\end{aligned}
\end{equation}
We identify
\begin{equation}\label{eqn:qftLecture9:560}
–
{T^\nu}_\mu =
-\partial^\nu \phi \partial_\mu \phi + {\delta^{\nu}}_\mu \LL,
\end{equation}
so the current is
\begin{equation}\label{eqn:qftLecture9:580}
\begin{aligned}
j^\nu_{\omega_{\mu\rho}}
&=
-\omega^{\mu\rho} x_\rho
{T^\nu}_\mu \\
&=
-\omega_{\mu\rho} x^\rho
T^{\nu\mu}
.
\end{aligned}
\end{equation}
Define
\begin{equation}\label{eqn:qftLecture9:600}
j^{\nu\mu\rho} = \inv{2} \lr{ x^\rho T^{\nu\mu} – x^{\mu} T^{\nu\rho} },
\end{equation}
which retains the antisymmetry in \( \mu \rho \) yet still drops the parameter \( \omega^{\mu\rho} \).
To check that this makes sense, we can contract
\( j^{\nu\mu\rho} \) with \( \omega_{\rho\mu} \)
\begin{equation}\label{eqn:qftLecture9:880}
\begin{aligned}
j^{\nu\mu\rho} \omega_{\rho\mu}
&= -\inv{2} \lr{ x^\rho T^{\nu\mu} – x^{\mu} T^{\nu\rho} }
\omega_{\mu\rho} \\
&=
-\inv{2} x^\rho T^{\nu\mu}
\omega_{\mu\rho}
– \inv{2} x^{\mu} T^{\nu\rho}
\omega_{\rho\mu} \\
&=
-\inv{2} x^\rho T^{\nu\mu}
\omega_{\mu\rho}
– \inv{2} x^{\rho} T^{\nu\mu}
\omega_{\mu\rho} \\
&=
– x^{\rho} T^{\nu\mu}
\omega_{\mu\rho},
\end{aligned}
\end{equation}
which matches \ref{eqn:qftLecture9:580} as desired.
Example. Rotations \( \mu\rho = ij \)
\begin{equation}\label{eqn:qftLecture9:620}
\begin{aligned}
J^{0 i j} \epsilon_{ijk}
&=
\inv{2} \lr{ x^i T^{0j} – x^{j} T^{0i} } \epsilon_{ijk} \\
&=
x^i T^{0j} \epsilon_{ijk}.
\end{aligned}
\end{equation}
Observe that this has the structure of \( (\Bx \cross \Bp)_k \), where \( \Bp \) is the momentum density of the field.
Let
\begin{equation}\label{eqn:qftLecture9:640}
L_k \equiv Q_k = \int d^3 x J^{0ij} \epsilon_{ijk}.
\end{equation}
We can now quantize and build a generator
\begin{equation}\label{eqn:qftLecture9:660}
\begin{aligned}
\hatU(\Balpha)
&= e^{i \Balpha \cdot \hat{\BL}} \\
&= \exp\lr{i \alpha_k
\int d^3 x x^i \hat{T}^{0j} \epsilon_{ijk}
}
\end{aligned}
\end{equation}
From \ref{eqn:qftLecture9:560} we can quantize with \( T^{0j} = \partial^0 \phi \partial^j \phi \rightarrow \hat{\pi} \lr{\spacegrad \phihat}_j\), or
\begin{equation}\label{eqn:qftLecture9:900}
\begin{aligned}
\hatU(\Balpha)
&=
\exp\lr{i \alpha_k
\int d^3 x x^i \hat{\pi} (\spacegrad \phihat)_j \epsilon_{ijk}
} \\
&=
\exp\lr{i \Balpha \cdot
\int d^3 x \hat{\pi} \spacegrad \phihat \cross \Bx
}
\end{aligned}
\end{equation}
(up to a sign in the exponent which doesn’t matter)
\begin{equation}\label{eqn:qftLecture9:680}
\begin{aligned}
\phihat(\By) \rightarrow \hatU(\alpha) \phihat(\By) \hatU^\dagger(\alpha)
&\approx
\phihat(\By) +
i \Balpha \cdot
\antisymmetric{
\int d^3 x \hat{\pi}(\Bx) \spacegrad \phihat(\Bx) \cross \Bx
}
{
\phihat(\By)
} \\
&=
\phihat(\By) +
i \Balpha \cdot
\int d^3 x
(-i) \delta^3(\Bx – \By)
\spacegrad \phihat(\Bx) \cross \Bx \\
&=
\phihat(\By) +
\Balpha \cdot \lr{ \spacegrad \phihat(\By ) \cross \By}
\end{aligned}
\end{equation}
Explicitly, in coordinates, this is
\begin{equation}\label{eqn:qftLecture9:700}
\begin{aligned}
\phihat(\By)
&\rightarrow
\phihat(\By) +
\alpha^i
\lr{
\partial^j \phihat(\By) y^k \epsilon_{jki}
} \\
&=
\phihat(\By) –
\epsilon_{ikj} \alpha^i y^k \partial^j \phihat \\
&=
\phihat( y^j – \epsilon^{ikj} \alpha^i y^k ).
\end{aligned}
\end{equation}
This is a rotation. To illustrate, pick \( \Balpha = (0, 0, \alpha) \), so \( y^j \rightarrow y^j – \epsilon^{ikj} \alpha y^k \delta_{i3} = y^j – \epsilon^{3kj} \alpha y^k \), or
\begin{equation}\label{eqn:qftLecture9:n}
\begin{aligned}
y^1 &\rightarrow y^1 – \epsilon^{3k1} \alpha y^k = y^1 + \alpha y^2 \\
y^2 &\rightarrow y^2 – \epsilon^{3k2} \alpha y^k = y^2 – \alpha y^1 \\
y^3 &\rightarrow y^3 – \epsilon^{3k3} \alpha y^k = y^3,
\end{aligned}
\end{equation}
or in matrix form
\begin{equation}\label{eqn:qftLecture9:720}
\begin{bmatrix}
y^1 \\
y^2 \\
y^3 \\
\end{bmatrix}
\rightarrow
\begin{bmatrix}
1 & \alpha & 0 \\
-\alpha & 1 & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
y^1 \\
y^2 \\
y^3 \\
\end{bmatrix}.
\end{equation}