ece1254

ECE1254H Modeling of Multiphysics Systems. Lecture 2: Assembling system equations automatically. Taught by Prof. Piero Triverio

September 23, 2014 ece1254 , ,

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

Assembling system equations automatically. Node/branch method

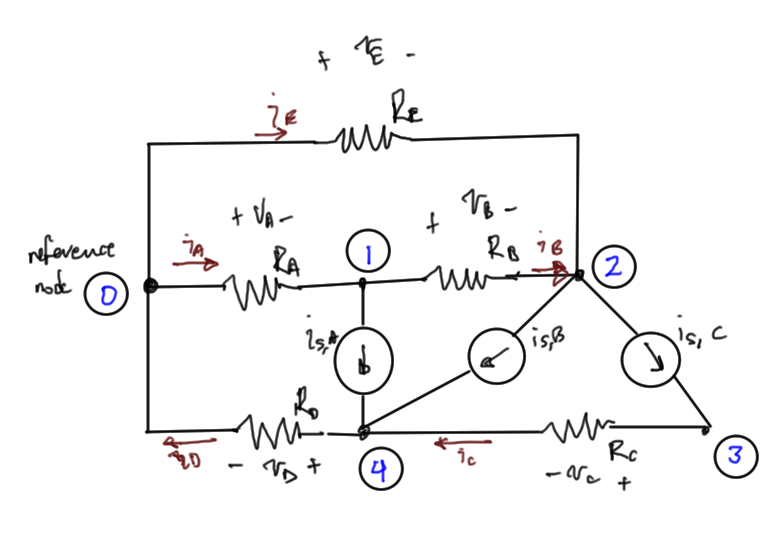
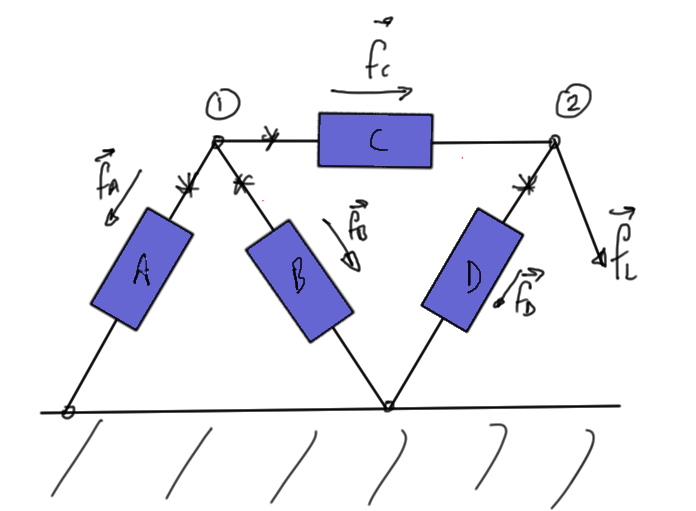
Consider the sample circuit of fig. 1.

fig. 1. Sample resistive circuit

fig. 1. Sample resistive circuit

Step 1. Choose unknowns:

For this problem, let’s take

  • node voltages: \(V_1, V_2, V_3, V_4\)

  • branch currents: \(i_A, i_B, i_C, i_D, i_E\)

We do not need to introduce additional labels for the source current sources.
We always introduce a reference node and call that zero.

For a circuit with \(N\) nodes, and \(B\) resistors, there will be \(N-1\) unknown node voltages and \(B\) unknown branch currents, for a total number of \(N – 1 + B\) unknowns.

Step 2. Conservation equations:

KCL

  • 0: \(i_A + i_E – i_D = 0\)
  • 1: \(-i_A + i_B + i_{S,A} = 0\)
  • 2: \(-i_B + i_{S,B} – i_E + i_{S,C} = 0\)
  • 3: \(i_C – i_{S,C} = 0\)
  • 4: \(-i_{S,A} – i_{S,B} + i_D – i_C = 0\)

Grouping unknown currents, this is

  • 0: \(i_A + i_E – i_D = 0\)
  • 1: \(-i_A + i_B = -i_{S,A}\)
  • 2: \(-i_B -i_E = -i_{S,B} -i_{S,C}\)
  • 3: \(i_C = i_{S,C}\)
  • 4: \(i_D – i_C = i_{S,A} + i_{S,B}\)

Note that one of these equations is redundant (sum 1-4). In a circuit with \(N\) nodes, we can write at most \(N-1\) independent KCLs.

In matrix form

\begin{equation}\label{eqn:multiphysicsL2:20}
\begin{bmatrix}
-1 & 1 & 0 & 0 & 0 \\
0 & -1 & 0 & 0 & -1 \\
0 & 0 & 1 & 0 & 0 \\
0 & 0 & -1 & 1 & 0
\end{bmatrix}
\begin{bmatrix}
i_A \\
i_B \\
i_C \\
i_D \\
i_E \\
\end{bmatrix}
=
\begin{bmatrix}
-i_{S,A} \\
-i_{S,B} -i_{S,C} \\
i_{S,C} \\
i_{S,A} + i_{S,B}
\end{bmatrix}
\end{equation}

We call this first matrix of ones and minus ones the incidence matrix \(A\). This matrix has \(B\) columns and \(N-1\) rows. We call the known current matrix \(\overline{I}_S\), and the branch currents \(\overline{I}_B\). That is

\begin{equation}\label{eqn:multiphysicsL2:40}
A \overline{I}_B = \overline{I}_S.
\end{equation}

Observe that we have both a plus and minus one in all columns except for those columns impacted by our neglect of the reference node current conservation equation.

Algorithm for filling \(A\)

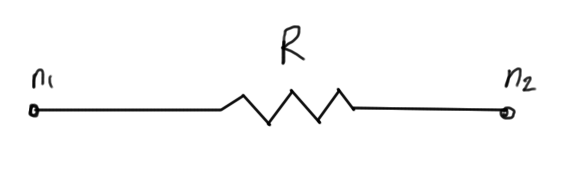
In the input file, to describe a resistor of fig. 2, you’ll have a line of the form

R name \(n_1\) \(n_2\) value

fig. 2. Resistor node convention

fig. 2. Resistor node convention

The algorithm to process resistor lines is

\begin{equation*}
\begin{aligned}
&A \leftarrow 0 \\
&ic \leftarrow 0 \\
&\text{forall resistor lines} \\
&ic \leftarrow ic + 1, \text{adding one column to \(A\)} \\
&\text{if}\ n_1 != 0 \\
&A(n_1, ic) \leftarrow +1 \\
&\text{endif} \\
&\text{if}\ n_2 != 0 \\
&A(n_2, ic) \leftarrow -1 \\
&\text{endif} \\
&\text{endfor} \\
\end{aligned}
\end{equation*}

Algorithm for filling \(\overline{I}_S\)

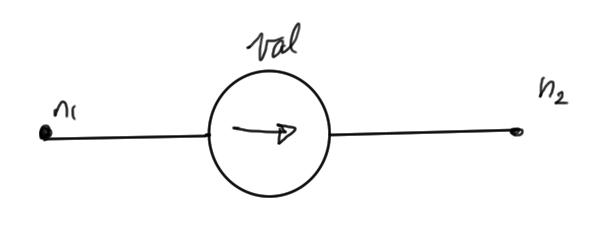
Current sources, as in fig. 3, a line will have the specification (FIXME: confirm… didn’t write this down).

I name \(n_1\) \(n_2\) value

fig. 3. Current source conventions

fig. 3. Current source conventions

\begin{equation*}
\begin{aligned}
&\overline{I}_S = \text{zeros}(N-1, 1) \\
&\text{forall current lines} \\
&\overline{I}_S(n_1) \leftarrow \overline{I}_S(n_1) – \text{value} \\
&\overline{I}_S(n_2) \leftarrow \overline{I}_S(n_1) + \text{value} \\
&\text{endfor}
\end{aligned}
\end{equation*}

Step 3. Constitutive equations:

\begin{equation}\label{eqn:multiphysicsL2:60}
\begin{bmatrix}
i_A \\
i_B \\
i_C \\
i_D \\
i_E
\end{bmatrix}
=
\begin{bmatrix}
1/R_A & & & & \\
& 1/R_B & & & & \\
& & 1/R_C & & & \\
& & & 1/R_D & & \\
& & & & & 1/R_E
\end{bmatrix}
\begin{bmatrix}
v_A \\
v_B \\
v_C \\
v_D \\
v_E
\end{bmatrix}
\end{equation}

Or

\begin{equation}\label{eqn:multiphysicsL2:80}
\overline{I}_B = \alpha \overline{V}_B,
\end{equation}

where \(\overline{V}_B\) are the branch voltages, not unknowns of interest directly. We can write

\begin{equation}\label{eqn:multiphysicsL2:100}
\begin{bmatrix}
v_A \\
v_B \\
v_C \\
v_D \\
v_E
\end{bmatrix}
=
\begin{bmatrix}
-1 & & & \\
1 & -1 & & \\
& & 1 & -1 \\
& & & 1 \\
& -1 & &
\end{bmatrix}
\begin{bmatrix}
v_1 \\
v_2 \\
v_3 \\
v_4
\end{bmatrix}
\end{equation}

Observe that this is the transpose of \(A\), allowing us to write

\begin{equation}\label{eqn:multiphysicsL2:120}
\overline{V}_B = A^\T \overline{V}_N.
\end{equation}

Solving

  • KCLs: \(A \overline{I}_B = \overline{I}_S\)

  • constitutive: \(\overline{I}_B = \alpha \overline{V}_B \Rightarrow \overline{I}_B = \alpha A^\T \overline{V}_N\)

  • branch and node voltages: \(\overline{V}_B = A^\T \overline{V}_N\)

In block matrix form, this is

\begin{equation}\label{eqn:multiphysicsL2:140}
\begin{bmatrix}
A & 0 \\
I & -\alpha A^\T
\end{bmatrix}
\begin{bmatrix}
\overline{I}_B \\
\overline{V}_N
\end{bmatrix}
=
\begin{bmatrix}
\overline{I}_S \\
0
\end{bmatrix}.
\end{equation}

Is it square? We see that it is after observing that we have

  • \(N-1\) rows in \(A\) , and \(B\) columns.
  • \(B\) rows in \(I\).
  • \(N-1\) columns.

ECE1254H Modeling of Multiphysics Systems. Lecture 1: Analogies to circuit systems. Taught by Prof. Piero Triverio

September 22, 2014 ece1254

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. May not be entirely coherent.

In slides

A review of systematic nodal analysis for a basic resistive circuit was outlined in slides, with a subsequent attempt to show how many similar linear systems can be modeled as circuits so that the same toolbox can be applied. This included blood flow through a body (and blood flow to the brain), a model of antenna interference in a portable phone, heat conduction in a one dimensional conductor under a heat lamp, and a few other systems.

This discussion reminded me of the joke where the farmer, the butcher and the physicist are all invited to talk at a beef convention. After meaningful and appropriate talks by the farmer and the butcher, the physicist gets his chance, and proceeds with “We begin by modeling the cow as a sphere, …”. The ECE equivalent of that appears to be a Kirchhoff circuit problem.

Mechanical structures example

Continuing the application of circuits like linear systems to other systems, let’s consider a truss system as illustrated in fig. 1, or in the simpler similar system of fig. 2.

fig. 1. A static loaded truss configuratio

fig. 1. A static loaded truss configuratio

fig 2. Simple static load

fig 2. Simple static load

Our unknowns are

  • positions of the joints after deformation \((x_i, y_i)\).
  • force acting on each strut \(\BF_j = (F_{j,x}, F_{j,y})\).

The constitutive equations, assuming static conditions (steady state, no transients)

  • Load force. \(\BF_L = (F_{L, x}, F_{L, y}) = (0, -m g)\).
  • Strut forces. Under static conditions the total resulting force on the strut is zero, so \(\BF’_j = -\BF_j\). For this problem it is redundant to label forces on both ends, so we mark the labeled end of the object with an asterisk as in fig. 3.
fig 3. Strut model

fig 3. Strut model

Consider a simple case

One strut as in fig. 4.

fig. 4. Very simple static load

fig. 4. Very simple static load

\begin{equation}\label{eqn:multiphysicsL1:20}
\BF^\conj = – \Ba_x
\underbrace{
\epsilon
}_{\text{constant, describes the beam elasticity, given}}
\biglr{
\underbrace{
L
}_{\text{unloaded length \(L = \Abs{x^\conj – 0}\), given}}
– L_0}
\end{equation}

The constitutive law for a general strut as in fig. 5 is

fig 5. Strut force diagram

fig 5. Strut force diagram

The force is directed along the unit vector

\begin{equation}\label{eqn:multiphysicsL1:40}
\Be = \frac{\Br^\conj – \Br}{\Abs{\Br^\conj – \Br}},
\end{equation}

and has the form
\begin{equation}\label{eqn:multiphysicsL1:60}
\BF^\conj = – \Be \epsilon \lr{ L – L_0 }.
\end{equation}

The value \(\epsilon\) may be related to Hooks’ constant, and \(L_0\) is given by

\begin{equation}\label{eqn:multiphysicsL1:80}
L = \Abs{\Br^\conj – \Br} = \sqrt{(x^\conj – x)^2 + (y^\conj – y)^2}.
\end{equation}

Observe that the relation between \(\BF^\conj\) and position is nonlinear!

Treatment of this system will be used as the prototype for our handling of other nonlinear systems.

Returning to the simple static system, and introducing force and joint labels as in fig. 6, we can examine the \textAndIndex{conservation law}, the balance of forces.

fig 6. Strut system

fig 6. Strut system

  • At joint 1:\begin{equation}\label{eqn:multiphysicsL1:100}
    \Bf_A + \Bf_B + \Bf_C = 0
    \end{equation}or
    \begin{equation}\label{eqn:multiphysicsL1:120}
    \begin{aligned}
    \Bf_{A,x} + \Bf_{B,x} + \Bf_{C,x} &= 0 \\
    \Bf_{A,y} + \Bf_{B,y} + \Bf_{C,y} &= 0
    \end{aligned}
    \end{equation}
  • At joint 2:\begin{equation}\label{eqn:multiphysicsL1:140}
    -\Bf_C + \Bf_D + \Bf_L = 0
    \end{equation}or
    \begin{equation}\label{eqn:multiphysicsL1:160}
    \begin{aligned}
    -\Bf_{C,x} + \Bf_{D,x} + \Bf_{L,x} &= 0 \\
    -\Bf_{C,y} + \Bf_{D,y} + \Bf_{L,y} &= 0
    \end{aligned}
    \end{equation}

We have an equivalence

  • Force \(\leftrightarrow\) Current.
  • Force balance equation \(\leftrightarrow\) KCL