ellipse

ECE1505H Convex Optimization. Lecture 4: Sets and convexity. Taught by Prof. Stark Draper

January 25, 2017 ece1505 , , , , , , ,

ECE1505H Convex Optimization. Lecture 4: Sets and convexity. Taught by Prof. Stark Draper

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

These are notes for the UofT course ECE1505H, Convex Optimization, taught by Prof. Stark Draper, covering [1] content.

Today

  • more on various sets: hyperplanes, half-spaces, polyhedra, balls, ellipses, norm balls, cone of PSD
  • generalize inequalities
  • operations that preserve convexity
  • separating and supporting hyperplanes.

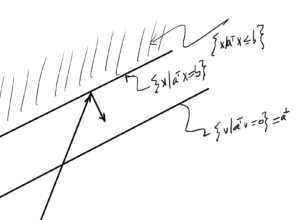
Hyperplanes

Find some \( \Bx_0 \in \mathbb{R}^n \) such that \( \Ba^\T \Bx_0 = \Bb \), so

\begin{equation}\label{eqn:convexOptimizationLecture4:20}
\begin{aligned}
\setlr{ \Bx | \Ba^\T \Bx = \Bb }
&=
\setlr{ \Bx | \Ba^\T \Bx = \Ba^\T \Bx_0 } \\
&=
\setlr{ \Bx | \Ba^\T (\Bx – \Bx_0) } \\
&=
\Bx_0 + \Ba^\perp,
\end{aligned}
\end{equation}

where

\begin{equation}\label{eqn:convexOptimizationLecture4:40}
\Ba^\perp = \setlr{ \Bv | \Ba^\T \Bv = 0 }.
\end{equation}

fig. 1. Parallel hyperplanes.

 

Recall

\begin{equation}\label{eqn:convexOptimizationLecture4:60}
\Norm{\Bz}_\conj = \sup_\Bx \setlr{ \Bz^\T \Bx | \Norm{\Bx} \le 1 }
\end{equation}

Denote the optimizer of above as \( \Bx^\conj \). By definition

\begin{equation}\label{eqn:convexOptimizationLecture4:80}
\Bz^\T \Bx^\conj \ge \Bz^\T \Bx \quad \forall \Bx, \Norm{\Bx} \le 1
\end{equation}

This defines a half space in which the unit ball

\begin{equation}\label{eqn:convexOptimizationLecture4:100}
\setlr{ \Bx | \Bz^\T (\Bx – \Bx^\conj \le 0 }
\end{equation}

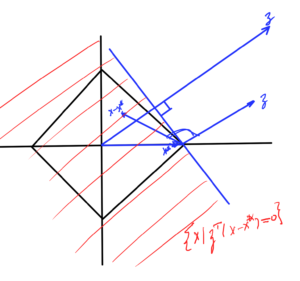
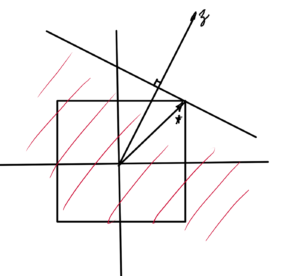
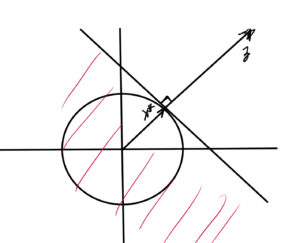
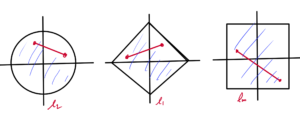
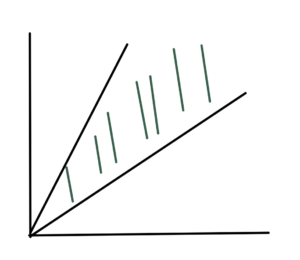
Start with the \( l_1 \) norm, duals of \( l_1 \) is \( l_\infty \)

 

fig. 2. Half space containing unit ball.

Similar pic for \( l_\infty \), for which the dual is the \( l_1 \) norm, as sketched in fig. 3.  Here the optimizer point is at \( (1,1) \)

 

fig. 3. Half space containing the unit ball for l_infinity

and a similar pic for \( l_2 \), which is sketched in fig. 4.

 

fig. 4. Half space containing for l_2 unit ball.

Q: What was this optimizer point?

Polyhedra

\begin{equation}\label{eqn:convexOptimizationLecture4:120}
\begin{aligned}
\mathcal{P}
&= \setlr{ \Bx |
\Ba_j^\T \Bx \le \Bb_j, j \in [1,m],
\Bc_i^\T \Bx = \Bd_i, i \in [1,p]
} \\
&=
\setlr{ \Bx | A \Bx \le \Bb, C \Bx = d },
\end{aligned}
\end{equation}

where the final inequality and equality are component wise.

Proving \( \mathcal{P} \) is convex:

  • Pick \(\Bx_1 \in \mathcal{P}\), \(\Bx_2 \in \mathcal{P} \)
  • Pick any \(\theta \in [0,1]\)
  • Test \( \theta \Bx_1 + (1-\theta) \Bx_2 \). Is it in \(\mathcal{P}\)?

\begin{equation}\label{eqn:convexOptimizationLecture4:140}
\begin{aligned}
A \lr{ \theta \Bx_1 + (1-\theta) \Bx_2 }
&=
\theta A \Bx_1 + (1-\theta) A \Bx_2 \\
&\le
\theta \Bb + (1-\theta) \Bb \\
&=
\Bb.
\end{aligned}
\end{equation}

Balls

Euclidean ball for \( \Bx_c \in \mathbb{R}^n, r \in \mathbb{R} \)

\begin{equation}\label{eqn:convexOptimizationLecture4:160}
\mathcal{B}(\Bx_c, r)
= \setlr{ \Bx | \Norm{\Bx – \Bx_c}_2 \le r },
\end{equation}

or
\begin{equation}\label{eqn:convexOptimizationLecture4:180}
\mathcal{B}(\Bx_c, r)
= \setlr{ \Bx | \lr{\Bx – \Bx_c}^\T \lr{\Bx – \Bx_c} \le r^2 }.
\end{equation}

Let \( \Bx_1, \Bx_2 \), \(\theta \in [0,1]\)

\begin{equation}\label{eqn:convexOptimizationLecture4:200}
\begin{aligned}
\Norm{ \theta \Bx_1 + (1-\theta) \Bx_2 – \Bx_c }_2
&=
\Norm{ \theta (\Bx_1 – \Bx_c) + (1-\theta) (\Bx_2 – \Bx_c) }_2 \\
&\le
\Norm{ \theta (\Bx_1 – \Bx_c)}_2 + \Norm{(1-\theta) (\Bx_2 – \Bx_c) }_2 \\
&=
\Abs{\theta} \Norm{ \Bx_1 – \Bx_c}_2 + \Abs{1 -\theta} \Norm{ \Bx_2 – \Bx_c }_2 \\
&=
\theta \Norm{ \Bx_1 – \Bx_c}_2 + \lr{1 -\theta} \Norm{ \Bx_2 – \Bx_c }_2 \\
&\le
\theta r + (1 – \theta) r \\
&= r
\end{aligned}
\end{equation}

Ellipse

\begin{equation}\label{eqn:convexOptimizationLecture4:220}
\mathcal{E}(\Bx_c, P)
=
\setlr{ \Bx | (\Bx – \Bx_c)^\T P^{-1} (\Bx – \Bx_c) \le 1 },
\end{equation}

where \( P \in S^n_{++} \).

  • Euclidean ball is an ellipse with \( P = I r^2 \)
  • Ellipse is image of Euclidean ball \( \mathcal{B}(0,1) \) under affine mapping.

 

fig. 5. Circle and ellipse.

Given

\begin{equation}\label{eqn:convexOptimizationLecture4:240}
F(\Bu) = P^{1/2} \Bu + \Bx_c
\end{equation}

\begin{equation}\label{eqn:convexOptimizationLecture4:260}
\begin{aligned}
\setlr{ F(\Bu) | \Norm{\Bu}_2 \le r }
&=
\setlr{ P^{1/2} \Bu + \Bx_c | \Bu^\T \Bu \le r^2 } \\
&=
\setlr{ \Bx | \Bx = P^{1/2} \Bu + \Bx_c, \Bu^\T \Bu \le r^2 } \\
&=
\setlr{ \Bx | \Bu = P^{-1/2} (\Bx – \Bx_c), \Bu^\T \Bu \le r^2 } \\
&=
\setlr{ \Bx | (\Bx – \Bx_c)^\T P^{-1} (\Bx – \Bx_c) \le r^2 }
\end{aligned}
\end{equation}

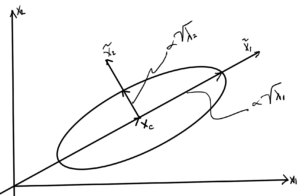
Geometry of an ellipse

Decomposition of positive definite matrix \( P \in S^n_{++} \subset S^n \) is:

\begin{equation}\label{eqn:convexOptimizationLecture4:280}
\begin{aligned}
P &= Q \textrm{diag}(\lambda_i) Q^\T \\
Q^\T Q &= 1
\end{aligned},
\end{equation}

where \( \lambda_i \in \mathbb{R}\), and \(\lambda_i > 0 \). The ellipse is defined by

\begin{equation}\label{eqn:convexOptimizationLecture4:300}
(\Bx – \Bx_c)^\T Q \textrm{diag}(1/\lambda_i) (\Bx – \Bx_c) Q \le r^2
\end{equation}

The term \( (\Bx – \Bx_c)^\T Q \) projects \( \Bx – \Bx_c \) onto the columns of \( Q \). Those columns are perpendicular since \( Q \) is an orthogonal matrix. Let

\begin{equation}\label{eqn:convexOptimizationLecture4:320}
\tilde{\Bx} = Q^\T (\Bx – \Bx_c),
\end{equation}

this shifts the origin around \( \Bx_c \) and \( Q \) rotates into a new coordinate system. The ellipse is therefore

\begin{equation}\label{eqn:convexOptimizationLecture4:340}
\tilde{\Bx}^\T
\begin{bmatrix}
\inv{\lambda_1} & & & \\
&\inv{\lambda_2} & & \\
& \ddots & \\
& & & \inv{\lambda_n}
\end{bmatrix}
\tilde{\Bx}
=
\sum_{i = 1}^n \frac{\tilde{x}_i^2}{\lambda_i} \le 1.
\end{equation}

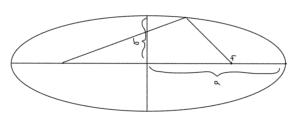
An example is sketched for \( \lambda_1 > \lambda_2 \) below.

 

Ellipse with \( \lambda_1 > \lambda_2 \).

  • \( \lambda_i \) tells us length of the semi-major axis.
  • Larger \( \lambda_i \) means \( \tilde{x}_i^2 \) can be bigger and still satisfy constraint \( \le 1 \).
  • Volume of ellipse if proportional to \( \sqrt{ \det P } = \sqrt{ \prod_{i = 1}^n \lambda_i } \).
  • When any \( \lambda_i \rightarrow 0 \) a dimension is lost and the volume goes to zero. That removes the invertibility required.

Ellipses will be seen a lot in this course, since we are interested in “bowl” like geometries (and the ellipse is the image of a Euclidean ball).

Norm ball.

The norm ball

\begin{equation}\label{eqn:convexOptimizationLecture4:360}
\mathcal{B} = \setlr{ \Bx | \Norm{\Bx} \le 1 },
\end{equation}

is a convex set for all norms. Proof:

Take any \( \Bx, \By \in \mathcal{B} \)

\begin{equation}\label{eqn:convexOptimizationLecture4:380}
\Norm{ \theta \Bx + (1 – \theta) \By }
\le
\Abs{\theta} \Norm{ \Bx } + \Abs{1 – \theta} \Norm{ \By }
=
\theta \Norm{ \Bx } + \lr{1 – \theta} \Norm{ \By }
\lr
\theta + \lr{1 – \theta}
=
1.
\end{equation}

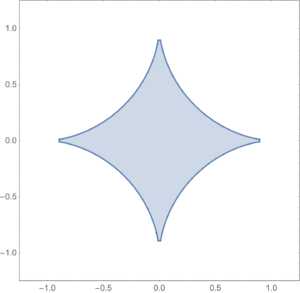
This is true for any p-norm \( 1 \le p \), \( \Norm{\Bx}_p = \lr{ \sum_{i = 1}^n \Abs{x_i}^p }^{1/p} \).

 

Norm ball.

The shape of a \( p < 1 \) norm unit ball is sketched below (lines connecting points in such a region can exit the region).

 

Cones

Recall that \( C \) is a cone if \( \forall \Bx \in C, \theta \ge 0, \theta \Bx \in C \).

Impt cone of PSD matrices

\begin{equation}\label{eqn:convexOptimizationLecture4:400}
\begin{aligned}
S^n &= \setlr{ X \in \mathbb{R}^{n \times n} | X = X^\T } \\
S^n_{+} &= \setlr{ X \in S^n | \Bv^\T X \Bv \ge 0, \quad \forall v \in \mathbb{R}^n } \\
S^n_{++} &= \setlr{ X \in S^n_{+} | \Bv^\T X \Bv > 0, \quad \forall v \in \mathbb{R}^n } \\
\end{aligned}
\end{equation}

These have respectively

  • \( \lambda_i \in \mathbb{R} \)
  • \( \lambda_i \in \mathbb{R}_{+} \)
  • \( \lambda_i \in \mathbb{R}_{++} \)

\( S^n_{+} \) is a cone if:

\( X \in S^n_{+}\), then \( \theta X \in S^n_{+}, \quad \forall \theta \ge 0 \)

\begin{equation}\label{eqn:convexOptimizationLecture4:420}
\Bv^\T (\theta X) \Bv
= \theta \Bv^\T \Bv
\ge 0,
\end{equation}

since \( \theta \ge 0 \) and because \( X \in S^n_{+} \).

Shorthand:

\begin{equation}\label{eqn:convexOptimizationLecture4:440}
\begin{aligned}
X &\in S^n_{+} \Rightarrow X \succeq 0
X &\in S^n_{++} \Rightarrow X \succ 0.
\end{aligned}
\end{equation}

Further \( S^n_{+} \) is a convex cone.

Let \( A \in S^n_{+} \), \( B \in S^n_{+} \), \( \theta_1, \theta_2 \ge 0, \theta_1 + \theta_2 = 1 \), or \( \theta_2 = 1 – \theta_1 \).

Show that \( \theta_1 A + \theta_2 B \in S^n_{+} \) :

\begin{equation}\label{eqn:convexOptimizationLecture4:460}
\Bv^\T \lr{ \theta_1 A + \theta_2 B } \Bv
=
\theta_1 \Bv^\T A \Bv
+\theta_2 \Bv^\T B \Bv
\ge 0,
\end{equation}

since \( \theta_1 \ge 0, \theta_2 \ge 0, \Bv^\T A \Bv \ge 0, \Bv^\T B \Bv \ge 0 \).

 

fig. 8. Cone.

Inequalities:

Start with a proper cone \( K \subseteq \mathbb{R}^n \)

  • closed, convex
  • non-empty interior (“solid”)
  • “pointed” (contains no lines)

The \( K \) defines a generalized inequality in \R{n} defined as “\(\le_K\)”

Interpreting

\begin{equation}\label{eqn:convexOptimizationLecture4:480}
\begin{aligned}
\Bx \le_K \By &\leftrightarrow \By – \Bx \in K
\Bx \end{aligned}
\end{equation}

Why pointed? Want if \( \Bx \le_K \By \) and \( \By \le_K \Bx \) with this \( K \) is a half space.

Example:1: \( K = \mathbb{R}^n_{+}, \Bx \in \mathbb{R}^n, \By \in \mathbb{R}^n \)

 

fig. 12. K is non-negative “orthant”

\begin{equation}\label{eqn:convexOptimizationLecture4:500}
\Bx \le_K \By \Rightarrow \By – \Bx \in K
\end{equation}

say:

\begin{equation}\label{eqn:convexOptimizationLecture4:520}
\begin{bmatrix}
y_1 – x_1
y_2 – x_2
\end{bmatrix}
\in R^2_{+}
\end{equation}

Also:

\begin{equation}\label{eqn:convexOptimizationLecture4:540}
K = R^1_{+}
\end{equation}

(pointed, since it contains no rays)

\begin{equation}\label{eqn:convexOptimizationLecture4:560}
\Bx \le_K \By ,
\end{equation}

with respect to \( K = \mathbb{R}^n_{+} \) means that \( x_i \le y_i \) for all \( i \in [1,n]\).

Example:2: For \( K = PSD \subseteq S^n \),

\begin{equation}\label{eqn:convexOptimizationLecture4:580}
\Bx \le_K \By ,
\end{equation}

means that

\begin{equation}\label{eqn:convexOptimizationLecture4:600}
\By – \Bx \in K = S^n_{+}.
\end{equation}

  • Difference \( \By – \Bx \) is always in \( S \)
  • check if in \( K \) by checking if all eigenvalues \( \ge 0 \).
  • \( S^n_{++} \) is the interior of \( S^n_{+} \).

Interpretation:

\begin{equation}\label{eqn:convexOptimizationLecture4:620}
\begin{aligned}
\Bx \le_K \By &\leftrightarrow \By – \Bx \in K \\
\Bx \end{aligned}
\end{equation}

We’ll use these with vectors and matrices so often the \( K \) subscript will often be dropped, writing instead (for vectors)

\begin{equation}\label{eqn:convexOptimizationLecture4:640}
\begin{aligned}
\Bx \le \By &\leftrightarrow \By – \Bx \in \mathbb{R}^n_{+} \\
\Bx < \By &\leftrightarrow \By – \Bx \in \textrm{int} \mathbb{R}^n_{++}
\end{aligned}
\end{equation}

and for matrices

\begin{equation}\label{eqn:convexOptimizationLecture4:660}
\begin{aligned}
\Bx \le \By &\leftrightarrow \By – \Bx \in S^n_{+} \\
\Bx < \By &\leftrightarrow \By – \Bx \in \textrm{int} S^n_{++}.
\end{aligned}
\end{equation}

Intersection

Take the intersection of (perhaps infinitely many) sets \( S_\alpha \):

If \( S_\alpha \) is (affine,convex, conic) for all \( \alpha \in A \) then

\begin{equation}\label{eqn:convexOptimizationLecture4:680}
\cap_\alpha S_\alpha
\end{equation}

is (affine,convex, conic). To prove in homework:

\begin{equation}\label{eqn:convexOptimizationLecture4:700}
\mathcal{P} = \setlr{ \Bx | \Ba_i^\T \Bx \le \Bb_i, \Bc_j^\T \Bx = \Bd_j, \quad \forall i \cdots j }
\end{equation}

This is convex since the intersection of a bunch of hyperplane and half space constraints.

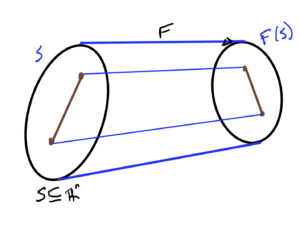
  1. If \( S \subseteq \mathbb{R}^n \) is convex then\begin{equation}\label{eqn:convexOptimizationLecture4:720}
    F(S) = \setlr{ F(\Bx) | \Bx \in S }
    \end{equation}is convex.
  2. If \( S \subseteq \mathbb{R}^m \) then\begin{equation}\label{eqn:convexOptimizationLecture4:740}
    F^{-1}(S) = \setlr{ \Bx | F(\Bx) \in S }
    \end{equation}is convex. Such a mapping is sketched in fig. 14.

 

fig. 14. Mapping functions of sets.

References

[1] Stephen Boyd and Lieven Vandenberghe. Convex optimization. Cambridge university press, 2004.

Circumference of an ellipse

March 9, 2015 math and physics play , , , ,

[Click here for a PDF of this post with nicer formatting]

Motivation

Lance told me they’ve been covering the circumference of a circle in school this week. This made me think of the generalization of a circle, the ellipse, but I couldn’t recall what the circumference of an ellipse was. Sofia guessed \( \pi ( a + b ) \). Her reasoning was that this goes to \( 2 \pi r \) when the ellipse is circular, just like the area of an ellipse \( \pi a b \), goes to \( \pi a^2 \) in the circular limit. That seemed reasonable to me, but also strange since I didn’t recall any \( \pi ( a + b ) \) formula.

It turns out that there’s no closed form expression for the circumference of an ellipse, unless you count infinite series or special functions. Here I’ll calculate one expression for this circumference.

Geometry recap

There’s two ways that I think of ellipses. One is the shape that you get when you put a couple tacks in a paper, and use a string and pencil to trace it out, as sketched in fig. 1.
The other is the basic vector parameterization of that same path

\begin{equation}\label{eqn:elipticCircumference:20}
\Br = ( a \cos\theta, b \sin\theta ).
\end{equation}

ellipseFig1

fig. 1. Ellipse, showing tracing curve from the foci.

 

It’s been a long time since grade 11 when I would have taken it for granted that these two representations are identical. To do so, we’d have to know where the foci of the ellipse sit. Cheating a bit I find in [1] that the foci are located at

\begin{equation}\label{eqn:elipticCircumference:40}
\Bf_{\pm} = \pm \sqrt{ a^2 – b^2 } (1, 0).
\end{equation}

This and the equivalence of the pencil and tack representation of the ellipse can be verified by checking that the “length of the string” equals \( 2 a \) as expected.

That string length is

\begin{equation}\label{eqn:elipticCircumference:60}
\begin{aligned}
\Abs{ \Br – \Bf_{+} } + \Abs{ \Br – \Bf_{-} }
&=
\sqrt{ (a \cos\theta – f)^2 + b^2 \sin^2\theta }
+
\sqrt{ (a \cos\theta + f)^2 + b^2 \sin^2\theta } \\
&=
\sqrt{ a^2 \cos^2 \theta + f^2 – 2 a f \cos\theta + b^2 \lr{ 1 – \cos^2\theta } } \\
&\quad +
\sqrt{ a^2 \cos^2 \theta + f^2 + 2 a f \cos\theta + b^2 \lr{ 1 – \cos^2\theta } }.
\end{aligned}
\end{equation}

These square roots simplify nicely

\begin{equation}\label{eqn:elipticCircumference:80}
\begin{aligned}
\sqrt{ a^2 \cos^2 \theta + f^2 \pm 2 a f \cos\theta + b^2 \lr{ 1 – \cos^2\theta } }
&=
\sqrt{ (a^2 – b^2) \cos^2 \theta + a^2 – b^2 \pm 2 a f \cos\theta + b^2 } \\
&=
\sqrt{ f^2 \cos^2 \theta + a^2 \pm 2 a f \cos\theta } \\
&=
\sqrt{ (a \pm f \cos\theta)^2 } \\
&=
a \pm f \cos\theta.
\end{aligned}
\end{equation}

So the total length from one focus to a point on the ellipse, back to the other focus, is

\begin{equation}\label{eqn:elipticCircumference:100}
\Abs{ \Br – \Bf_{+} } + \Abs{ \Br – \Bf_{-} }
=
a + f \cos\theta + a – f \cos\theta = 2 a,
\end{equation}

as expected. That verifies that the trigonometric parameterization matches with the pencil and tacks representation of an ellipse (provided the foci are placed at the points \ref{eqn:elipticCircumference:40}).

Calculating the circumference

The circumference expression can almost be written by inspection. An element of the tangent vector along the curve is

\begin{equation}\label{eqn:elipticCircumference:340}
\frac{d\Br}{d\theta} = ( -a \sin\theta, b \cos\theta ),
\end{equation}

so the circumference is just a one liner

\begin{equation}\label{eqn:elipticCircumference:280}
C = 4 \int_0^{\pi/2} \sqrt{ a^2 \sin^2\theta + b^2 \cos^2 \theta} d\theta.
\end{equation}

The problem is that this one liner isn’t easy to evaluate. The square root can be put in a slightly simpler form in terms of the eccentricity, which is defined by

\begin{equation}\label{eqn:elipticCircumference:300}
e = \frac{f}{a} = \frac{\sqrt{a^2 – b^2}}{a} = \sqrt{ 1 – \frac{b^2}{a^2} }.
\end{equation}

Factoring out \( a \) and writing the sine as a cosine gives

\begin{equation}\label{eqn:elipticCircumference:320}
\begin{aligned}
C
&=
4 a \int_0^{\pi/2} \sqrt{ 1 – \cos^2\theta + \frac{b^2}{a^2} \cos^2 \theta} d\theta \\
&=
4 a \int_0^{\pi/2} \sqrt{ 1 + \lr{ \frac{b^2}{a^2} -1} \cos^2 \theta} d\theta \\
&=
4 a \int_0^{\pi/2} \sqrt{ 1 – e^2 \cos^2 \theta} d\theta.
\end{aligned}
\end{equation}

For the square root, it’s not hard to show that the fractional binomial expansion is

\begin{equation}\label{eqn:elipticCircumference:360}
\sqrt{1 + a}
=
1 – \sum_{k=1}^\infty \frac{(-a)^k}{2k – 1}\frac{ (2k – 1)!!}{(2k)!!},
\end{equation}

so the circumference is

\begin{equation}\label{eqn:elipticCircumference:380}
C
=
4 a \int_0^{\pi/2} d\theta
\lr{ 1 – \sum_{k=1}^\infty \frac{(e \cos\theta)^{2k}}{2k – 1}\frac{ (2k – 1)!!}{(2k)!!}}.
\end{equation}

Using \ref{eqn:elipticCircumference:260}, this is

\begin{equation}\label{eqn:elipticCircumference:400}
C
=
2 \pi a
–
4 a
\sum_{k=1}^\infty \frac{e^{2k}}{2k – 1}\frac{ (2k – 1)!!}{(2k)!!}
\frac{(2k – 1)!!}{(2k)!!} \frac{\pi}{2}
\end{equation}

\begin{equation}\label{eqn:elipticCircumference:420}
\boxed{
C
=
2 \pi a \lr{ 1 –
\sum_{k=1}^\infty \frac{e^{2k}}{2k – 1} \lr{ \frac{ (2k – 1)!!}{(2k)!!} }^2
}.
}
\end{equation}

Observe that this does reduce to \( 2 \pi r \) for the circle (where \( e = 0 \)), and certainly isn’t as nice as \( \pi (a + b) \).

Appendix. Integral of even cosine powers.

The integral

\begin{equation}\label{eqn:elipticCircumference:120}
\int_0^{\pi/2} \cos^{2k} \theta d\theta
\end{equation}

can be evaluated using integration by parts.

\begin{equation}\label{eqn:elipticCircumference:140}
\begin{aligned}
\int_0^{\pi/2} \cos^{2k} \theta d\theta
&=
\int_0^{\pi/2} \cos^{2k-1} \theta \frac{d \sin\theta}{d\theta} d\theta \\
&=
\evalrange{
\cos^{2k-1} \theta \sin\theta
}{0}{\pi/2}
–
(2 k -1)
\int_0^{\pi/2} \cos^{2k-2} \theta (-\sin\theta) \sin\theta d\theta \\
&=
(2 k -1)
\int_0^{\pi/2} \cos^{2k-2} \theta (1 – \cos^2\theta) d\theta \\
&=
(2 k -1)
\int_0^{\pi/2} \cos^{2k-2} \theta d\theta
–
(2 k -1)
\int_0^{\pi/2} \cos^{2k} \theta d\theta.
\end{aligned}
\end{equation}

Bringing the \( 2k \) power integral to the other side and solving for the original integral gives a recurrence relation

\begin{equation}\label{eqn:elipticCircumference:160}
\begin{aligned}
\int_0^{\pi/2} \cos^{2k} \theta d\theta
&= \frac{2 k – 1}{2 k}
\int_0^{\pi/2} \cos^{2k -2} \theta d\theta \\
&=
\frac{2 k – 1}{2 k}
\frac{2 k – 3}{2 k – 2}
\int_0^{\pi/2} \cos^{2k -4} \theta d\theta \\
&=
\frac{2 k – 1}{2 k}
\frac{2 k – 3}{2 k – 2}
\cdots
\frac{3}{4}
\int_0^{\pi/2} \cos^{2} \theta d\theta.
\end{aligned}
\end{equation}

This last can also be solved using integration by parts

\begin{equation}\label{eqn:elipticCircumference:180}
\begin{aligned}
\int_0^{\pi/2} \cos^{2} \theta d\theta
&=
\int_0^{\pi/2} \cos \theta \frac{d \sin\theta}{d\theta} d\theta \\
&=
–
\int_0^{\pi/2} (-\sin \theta) \sin\theta d\theta \\
&=
\int_0^{\pi/2} \lr{ 1 – \cos^2 \theta } d\theta,
\end{aligned}
\end{equation}

or

\begin{equation}\label{eqn:elipticCircumference:200}
\begin{aligned}
\Abs{ \Br – \Bf_{+} } + \Abs{ \Br – \Bf_{-} }
&=
\int_0^{\pi/2} \cos^{2} \theta d\theta \\
&=
\inv{2} \frac{\pi}{2}.
\end{aligned}
\end{equation}

This gives

\begin{equation}\label{eqn:elipticCircumference:220}
\int_0^{\pi/2} \cos^{2k} \theta d\theta
=
\frac{2 k – 1}{2 k}
\frac{2 k – 3}{2 k – 2}
\cdots
\frac{3}{4}
\frac{1}{2}
\frac{\pi}{2}.
\end{equation}

Using the double factorial notation (factorial that skips every other value), this is

\begin{equation}\label{eqn:elipticCircumference:260}
\boxed{
\int_0^{\pi/2} \cos^{2k} \theta d\theta
=
\frac{(2k – 1)!!}{(2k)!!} \frac{\pi}{2}
}
\end{equation}

References

[1] Wikipedia. Ellipse — wikipedia, the free encyclopedia, 2015. URL https://en.wikipedia.org/w/index.php?title=Ellipse&oldid=650116160. [Online; accessed 9-March-2015].