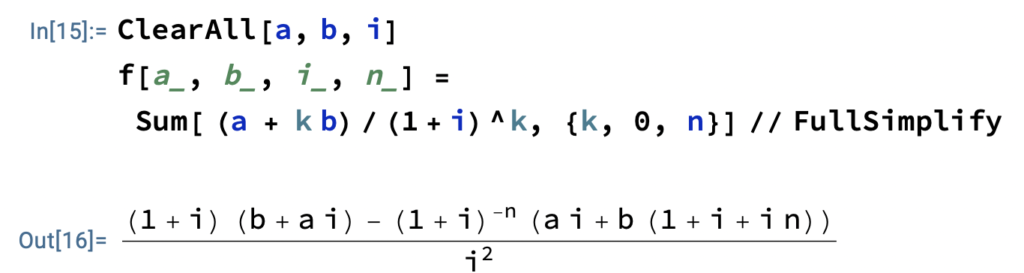[Click here for a PDF version of this post]
Karl needed to evaluate the sum:
\begin{equation}\label{eqn:weightedGeometric:20}
S = \sum_{k = 0}^9 \frac{a + b k}{\lr{ 1 + i }^k}
\end{equation}
He ended up using a spreadsheet, which was a quick and effective way to deal with the problem. I was curious about this sum, since he asked me how to sum it symbolically, and I didn’t know.
Mathematica doesn’t have any problem with it, as seen in fig. 1.
How can we figure this out?
Let’s write \( r = 1/(1+i) \) to start with, and break up the sum into constituent parts
\begin{equation}\label{eqn:weightedGeometric:40}
\begin{aligned}
S_n
&= \sum_{k = 0}^n \frac{a + b k}{\lr{ 1 + i }^k} \\
&= a \sum_{k = 0}^n r^k + b \sum_{k = 0}^n k r^k.
\end{aligned}
\end{equation}
We can evaluate the geometric part of this easily using the usual trick. Let
\begin{equation}\label{eqn:weightedGeometric:60}
T_n = \sum_{k = 0}^n r^k,
\end{equation}
then
\begin{equation}\label{eqn:weightedGeometric:80}
r T_n – T_n = r^{n+1} – 1,
\end{equation}
so
\begin{equation}\label{eqn:weightedGeometric:100}
T_n = \frac{r^{n+1} – 1}{r – 1}.
\end{equation}
Now we just have to figure out how to sum
\begin{equation}\label{eqn:weightedGeometric:120}
G_n = \sum_{k = 0}^n k r^k = \sum_{k = 1}^n k r^k.
\end{equation}
This looks suspiciously like the derivative of a geometric series. Let’s evaluate such a derivative, as a function of r:
\begin{equation}\label{eqn:weightedGeometric:140}
\begin{aligned}
\frac{d T_n(r)}{dr}
&= \sum_{k = 0}^n \frac{d}{dr} r^k \\
&= \sum_{k = 0}^n k r^{k-1} \\
&= \sum_{k = 1}^n k r^{k-1} \\
&= \inv{r} \sum_{k = 1}^n k r^k.
\end{aligned}
\end{equation}
Having summed the geometric series, we may also take the derivative of that summed result
\begin{equation}\label{eqn:weightedGeometric:160}
\begin{aligned}
\frac{d T_n(r)}{dr}
&= \frac{d}{dr} \lr{ \frac{r^{n+1} – 1}{r – 1} } \\
&= \frac{(n+1)r^n}{r – 1} – \frac{r^{n+1} – 1}{\lr{r -1}^2} \\
&= \frac{(n+1)r^n(r-1) – \lr{r^{n+1} – 1}}{\lr{r -1}^2}.
\end{aligned}
\end{equation}
Putting the pieces together, we have
\begin{equation}\label{eqn:weightedGeometric:180}
T_n = \frac{r}{\lr{r -1}^2} \lr{ (n+1)r^n(r-1) – \lr{r^{n+1} – 1} }.
\end{equation}
This means that our sum is
\begin{equation}\label{eqn:weightedGeometric:200}
S_n = a \frac{r^{n+1} – 1}{r – 1} + b \frac{r}{\lr{r -1}^2} \lr{ (n+1)r^n(r-1) – \lr{r^{n+1} – 1} }.
\end{equation}
Putting back \( r = 1/(1+i) \), and subsequent simplification, gives the Mathematica result. It’s not pretty, but at least we can do it if we want to.
Shout out to Grok that pointed out the derivative trick for the second series. I’d forgotten that one.