[Click here for a PDF version of this post]

Another problem from x/twitter [1]:

Find \( k \), where
\begin{equation}\label{eqn:trigProp:20}
\int_0^{2 \pi} \sin^4 x dx = k \int_0^{\pi/2} \cos^4 x dx.
\end{equation}
I initially misread the integration range in the second integral as \( 2 \pi \), not \( \pi/2 \), in which case the answer is just 1 by inspection. However, solving the stated problem, is not much more difficult.

Since sine and cosine are equal up to a shift by \( \pi/2 \)
\begin{equation}\label{eqn:trigProp:40}
\sin(u + \pi/2) = \frac{e^{i(u + \pi/2)} – e^{-i(u + \pi/2)}}{2i} = \frac{e^{i u} + e^{-i u}}{2} = \cos u,
\end{equation}
we can make an \( x = u + \pi/2 \) substitution in the sine integral.

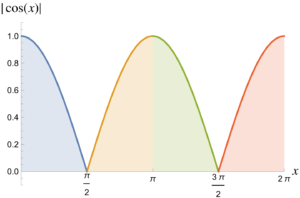
Observe that \( \cos^4 x = \Abs{\cos x}^4 \), but the area under \( \Abs{\cos x} \) is the same for each \( \pi/2 \) interval. This is shown in fig. 1.

fig. 1. Plot of |cos x|

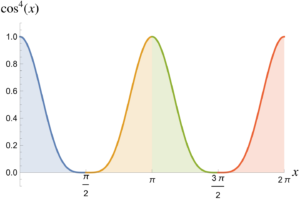
Of course, the area under \( \cos^4 x \), will also have the same periodicity, but those regions will be rounded out by the power operation, as shown in fig. 2.

fig. 2. Plot of cos^4 x.

Since the area under \( \cos^4 x \) is the same for each \( \pi/2 \) wide interval, we have
\begin{equation}\label{eqn:trigProp:60}
\boxed{
k = 4.
}
\end{equation}

References

[1] CalcInsights. What will be the value of k to satisfy this integral equation, 2025. URL https://x.com/CalcInsights_/status/1880932308108341443. [Online; accessed 19-Jan-2025].