[Click here for a PDF version of this post]
Scalar equation for a hyperplane.
In our last post, we found, in a round about way, that
Theorem 1.1:
\begin{equation*}
\Bx \cdot \mathbf{\hat{n}} = d.
\end{equation*}
Start proof:
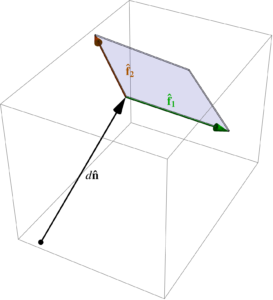
Let \( \beta = \setlr{ \mathbf{\hat{f}}_1, \cdots \mathbf{\hat{f}}_{N-1} } \) be an orthonormal basis for the hyperplane normal to \( \mathbf{\hat{n}} \), and \( \Bd = d \mathbf{\hat{n}} \) be the vector in that hyperplane, closest to the origin, as illustrated in fig. 1.
The hyperplane \( d \) distant from the origin with normal \( \mathbf{\hat{n}} \) has the parametric representation
\begin{equation}\label{eqn:hyperplaneGeometry:40}
\Bx(a_1, \cdots, a_{N-1}) = d \mathbf{\hat{n}} + \sum_{i = 1}^{N-1} a_i \mathbf{\hat{f}}_i.
\end{equation}
Equivalently, suppressing the parameterization, with \( \Bx = \Bx(a_1, \cdots, a_{N-1}) \), representing any vector in that hyperplane, by dotting with \( \mathbf{\hat{n}} \), we have
\begin{equation}\label{eqn:hyperplaneGeometry:60}
\Bx \cdot \mathbf{\hat{n}} = d \mathbf{\hat{n}} \cdot \mathbf{\hat{n}},
\end{equation}
where all the \( \mathbf{\hat{f}}_i \cdot \mathbf{\hat{n}} \) dot products are zero by construction. Since \( \mathbf{\hat{n}} \cdot \mathbf{\hat{n}} = 0 \), the proof is complete.
End proof.
Incidentally, observe we can also write the hyperplane equation in dual form, as
\begin{equation}\label{eqn:hyperplaneGeometry:220}
\Bx \wedge (\mathbf{\hat{n}} I) = d I,
\end{equation}
where \( I \) is an \(\mathbb{R}^N\) pseudoscalar (such as \( I = \mathbf{\hat{n}} \mathbf{\hat{f}}_1 \cdots \mathbf{\hat{f}}_{N-1} \)).
Our previous parallel plane separation problem.
The standard \(\mathbb{R}^3\) scalar form for an equation of a plane is
\begin{equation}\label{eqn:hyperplaneGeometry:80}
a x + b y + c z = d,
\end{equation}
where \( d \) looses it’s geometrical meaning. If we form \( \Bn = (a,b,c) \), then we can rewrite this as
\begin{equation}\label{eqn:hyperplaneGeometry:100}
\Bx \cdot \Bn = d,
\end{equation}
for this representation of an equation of a plane, we see that \( d/\Norm{\Bn} \) is the shortest distance from the origin to the plane. This means that if we have a pair of parallel plane equations
\begin{equation}\label{eqn:hyperplaneGeometry:120}
\begin{aligned}
\Bx \cdot \Bn &= d_1 \\
\Bx \cdot \Bn &= d_2,
\end{aligned}
\end{equation}
then the distance between those planes, by inspection, is
\begin{equation}\label{eqn:hyperplaneGeometry:140}
\Abs{ \frac{d_2}{\Norm{\Bn}} – \frac{d_1}{\Norm{\Bn}} },
\end{equation}
which reduces to just \( \Abs{d_2 – d_1} \) if \( \Bn \) is a unit normal for the plane. In our previous post, the problem to solve was to find the shortest distance between the parallel planes given by
\begin{equation}\label{eqn:hyperplaneGeometry:160}
\begin{aligned}
x – y + 2 z &= -3 \\
3 x – 3 y + 6 z &= 1.
\end{aligned}
\end{equation}
The more natural geometrical form for these plane equations is
\begin{equation}\label{eqn:hyperplaneGeometry:180}
\begin{aligned}
\Bx \cdot \mathbf{\hat{n}} &= -\frac{3}{\sqrt{6}} \\
\Bx \cdot \mathbf{\hat{n}} &= \inv{3 \sqrt{6}},
\end{aligned}
\end{equation}
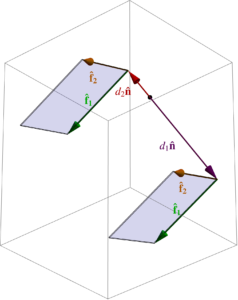
where \( \mathbf{\hat{n}} = (1,-1,2)/\sqrt{6} \), as illustrated in fig. 2.
Given that representation, we can find the distance between the planes just by taking the absolute difference of the respective distances to the origin
\begin{equation}\label{eqn:hyperplaneGeometry:200}
\begin{aligned}
\Abs{ -\frac{3}{\sqrt{6}} – \inv{3 \sqrt{6}} }
&= \frac{\sqrt{6}}{6} \lr{ 3 + \inv{3} } \\
&= \frac{10}{18} \sqrt{6} \\
&= \frac{5}{9} \sqrt{6}.
\end{aligned}
\end{equation}