[Click here for a PDF version of this post]
Here’s (31(d)) from [1]. Find
\begin{equation}\label{eqn:fourPoles:20}
I = \int_0^\infty \frac{dx}{1 + x^4} = \inv{2}\int_{-\infty}^\infty \frac{dx}{1 + x^4}.
\end{equation}
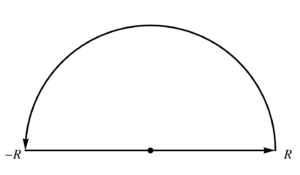
This one is easy conceptually, but a bit messy algebraically. We integrate over the contour \( C \) illustrated in fig. 1.
fig. 1. Standard above the x-axis, semicircular contour.
We want to evaluate
\begin{equation}\label{eqn:fourPoles:40}
2 I = \oint_C \frac{dz}{1 + z^4},
\end{equation}
because the semicircular part of the integral is \( O(R^{-3}) \), which tends to zero in the \( R \rightarrow \infty \) limit.
The poles are at the points
\begin{equation}\label{eqn:fourPoles:60}
\begin{aligned}
z^4
&= -1 \\
&= e^{i \pi + 2 \pi i k},
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:fourPoles:80}
\begin{aligned}
z
&= e^{i \pi/4 + \pi i k/2},
\end{aligned}
\end{equation}
These are the points \( z = (\pm 1 \pm i)/\sqrt{2} \), two of which are enclosed by our contour. Specifically
\begin{equation}\label{eqn:fourPoles:100}
\begin{aligned}
2 I
&= \oint_C \frac{dz}{
\lr{ z – \frac{1 + i}{\sqrt{2}} }
\lr{ z – \frac{-1 + i}{\sqrt{2}} }
\lr{ z – \frac{1 – i}{\sqrt{2}} }
\lr{ z – \frac{-1 – i}{\sqrt{2}} }
} \\
&= \oint_C \frac{dz}{
\lr{ z – \frac{1 + i}{\sqrt{2}} }
\lr{ z – \frac{-1 + i}{\sqrt{2}} }
\lr{ \lr{z + \frac{i}{\sqrt{2}}}^2 – \inv{2} }
} \\
&=
\evalbar{
\frac{ 2 \pi i }
{
\lr{ z – \frac{-1 + i}{\sqrt{2}} }
\lr{ \lr{z + \frac{i}{\sqrt{2}}}^2 – \inv{2} }
}
}{z = \frac{1 + i}{\sqrt{2}}}
+
\evalbar{
\frac{ 2 \pi i }
{
\lr{ z – \frac{1 + i}{\sqrt{2}} }
\lr{ \lr{z + \frac{i}{\sqrt{2}}}^2 – \inv{2} }
}
}
{z = \frac{-1 + i}{\sqrt{2}} } \\
&=
\evalbar{
\frac{(2 \pi i )(2 \sqrt{2})}
{
\lr{ z’ + 1 – i }
\lr{ \lr{z’ + i}^2 – 1 }
}
}{z’ = 1 + i}
+
\evalbar{
\frac{(2 \pi i )(2 \sqrt{2})}
{
\lr{ z’ – 1 – i }
\lr{ \lr{z’ + i}^2 – 1 }
}
}
{z’ = -1 + i}
\\
&=
\frac{2 \pi i \sqrt{2}}
{
\lr{2 i + 1}^2 – 1 }
–
\frac{2 \pi i \sqrt{2}}
{ \lr{2 i – 1}^2 – 1 }
\\
&=
\frac{\pi i \sqrt{2}}
{
2 (-1 + i)
}
+
\frac{\pi i \sqrt{2}}
{ 2(1 + i) }
\\
&=
\lr{ -1 – i }
\frac{\pi i}
{
2 \sqrt{2}
}
+
\lr{ 1 – i }
\frac{\pi i}
{ 2 \sqrt{2} }
\\
&=
\frac{\pi}
{ \sqrt{2} }
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:fourPoles:120}
\boxed{
I = \frac{\pi}{2 \sqrt{2}}.
}
\end{equation}
References
[1] F.W. Byron and R.W. Fuller. Mathematics of Classical and Quantum Physics. Dover Publications, 1992.