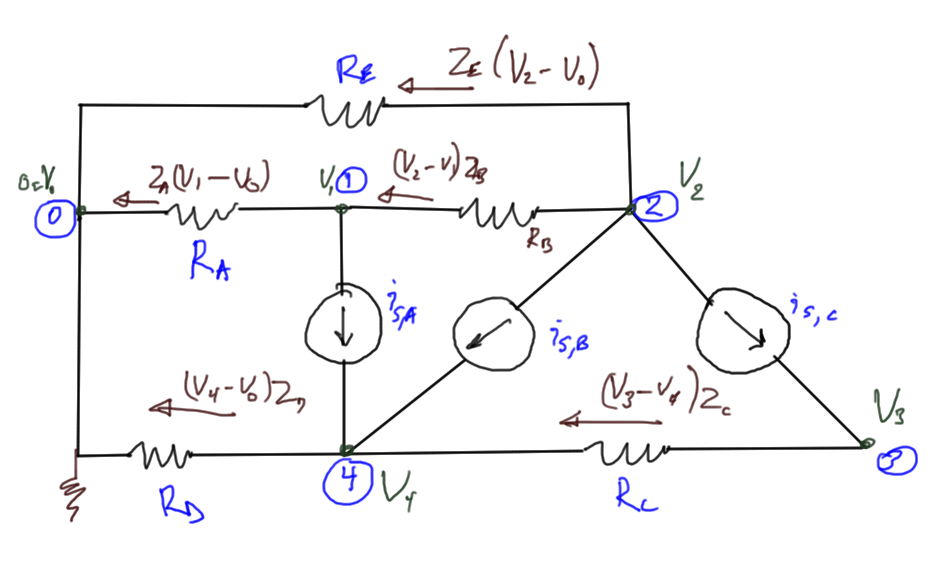
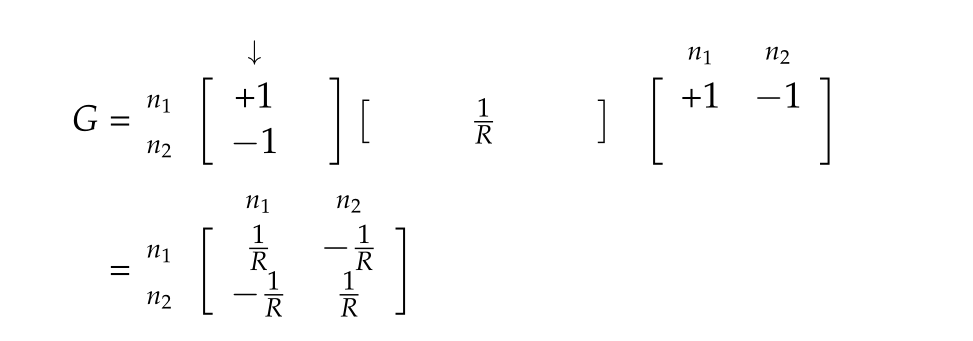
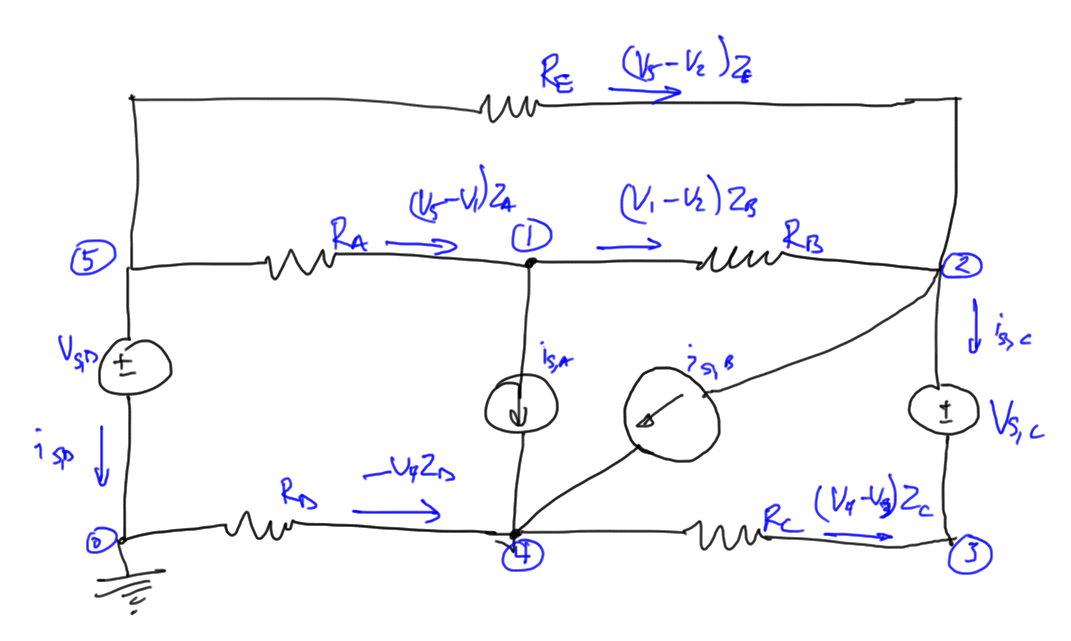
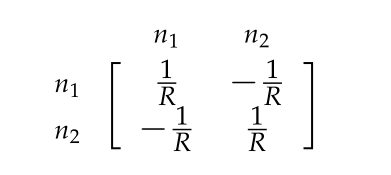The propaganda for celebration of war, destruction, killing, and rape is already starting. I was greeted today on facebook by the serene and smiling image of a world war II vet, along with his seemingly innocent request for “likes”
This is probably supposed to make people feel patriotism, the worship of an artificial boundary on a map and its associated label system. Patriotism and national pride worship are designed to ensure that no rational thought opposes the psychopathic figureheads that run our modern “democracies”.
When we see vet worship propaganda like this, you have to think about the interests that encouraged the war in the first place. These are power brokers like the Carnegies that requested that Wilson not end the war (WWI) too soon (and who had concluded in their minutes before that there was no better institution for profits than the business of war). These are the armaments and munitions manufacturers. These are the companies that built the tanks and the planes that bombed uncounted civilians in Germany and the UK. These are the makers of weapons that use white phosphorus and depleted uranium, and the makers of cluster bombs that shred children into hamburger meat before and after they are deployed.
I would describe us as being in world war III now. This is the series of undeclared and covert wars that the USA and NATO have waged since world war II. This is a war that happens with our tacit approval. This approval that is assumed because there is no widespread disapproval. Unfortunately, so much of this modern and current war happens without our even knowing about it, that nobody thinks to object. This war is disconnected from our immediate attention, and most of the time we don’t even realize that we are funding it. As always, I don’t want my tax dollars, money stolen from me at the point of a gun, to be used to fund the slaughter of people in Yugoslavia or Libya or <enter your favorite target in some little known corner of the world>, but I can’t control this. It happens again and again, and is truly disgusting.
I am happy to see that this poor fellow survived. However, if he had fought a real war, it would have been the war against the propaganda and brainwashing that involved him in the combat that got most of his compatriots killed, and against the same combat that killed uncountable numbers of civilians and “enemies”, and against the combat that encouraged these “enemies” to do the same.
I will not be liking this picture.