[Click here for a PDF of this post with nicer formatting]
Motivation
In class an outline of normal transmission through a slab was presented. Let’s go through the details.
Normal incidence
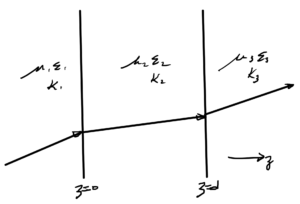
The geometry of a two interface configuration is sketched in fig. 1.
Given a normal incident ray with magnitude \( A \), the respective forward and backwards rays in each the mediums can be written as
- [I]
- \begin{equation}\label{eqn:twoInterfaceNormal:20}
\begin{aligned}
A e^{-j k_1 z} \\
A r e^{j k_1 z} \\
\end{aligned}
\end{equation} - \begin{equation}\label{eqn:twoInterfaceNormal:40}
C e^{-j k_2 z} \\
D e^{j k_2 z} \\
\end{equation} - \begin{equation}\label{eqn:twoInterfaceNormal:60}
A t e^{-j k_3 (z-d)}
\end{equation}
Matching at \( z = 0 \) gives
\begin{equation}\label{eqn:twoInterfaceNormal:80}
\begin{aligned}
A t_{12} + r_{21} D &= C \\
A r &= A r_{12} + D t_{21},
\end{aligned}
\end{equation}
whereas matching at \( z = d \) gives
\begin{equation}\label{eqn:twoInterfaceNormal:100}
\begin{aligned}
A t &= C e^{-j k_2 d} t_{23} \\
D e^{j k_2 d} &= C e^{-j k_2 d} r_{23}
\end{aligned}
\end{equation}
We have four linear equations in four unknowns \( r, t, C, D \), but only care about solving for \( r, t \). Let’s write \(
\gamma = e^{ j k_2 d }, C’ = C/A, D’ = D/A \), for
\begin{equation}\label{eqn:twoInterfaceNormal:120}
\begin{aligned}
t_{12} + r_{21} D’ &= C’ \\
r &= r_{12} + D’ t_{21} \\
t \gamma &= C’ t_{23} \\
D’ \gamma^2 &= C’ r_{23}
\end{aligned}
\end{equation}
Solving for \( C’, D’ \) we get
\begin{equation}\label{eqn:twoInterfaceNormal:140}
\begin{aligned}
D’ \lr{ \gamma^2 – r_{21} r_{23} } &= t_{12} r_{23} \\
C’ \lr{ \gamma^2 – r_{21} r_{23} } &= t_{12} \gamma^2,
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:twoInterfaceNormal:160}
\begin{aligned}
r &= r_{12} + \frac{t_{12} t_{21} r_{23} }{\gamma^2 – r_{21} r_{23} } \\
t &= t_{23} \frac{ t_{12} \gamma }{\gamma^2 – r_{21} r_{23} }.
\end{aligned}
\end{equation}
With \( \phi = -j k_2 d \), or \( \gamma = e^{-j\phi} \), we have
\begin{equation}\label{eqn:twoInterfaceNormal:180}
\boxed{
\begin{aligned}
r &= r_{12} + \frac{t_{12} t_{21} r_{23} e^{2 j \phi} }{1 – r_{21} r_{23} e^{2 j \phi}} \\
t &= \frac{ t_{12} t_{23} e^{j\phi}}{1 – r_{21} r_{23} e^{2 j \phi}}.
\end{aligned}
}
\end{equation}
A slab
When the materials in region I, and III are equal, then \( r_{12} = r_{32} \). For a TE mode, we have
\begin{equation}\label{eqn:twoInterfaceNormal:200}
r_{12}
=
\frac{\mu_2 k_{1z} – \mu_1 k_{2z}}{\mu_2 k_{1z} + \mu_1 k_{2z}}
= -r_{21}.
\end{equation}
so the reflection and transmission coefficients are
\begin{equation}\label{eqn:twoInterfaceNormal:220}
\begin{aligned}
r^{\textrm{TE}} &= r_{12} \lr{ 1 – \frac{t_{12} t_{21} e^{2 j \phi} }{1 – r_{21}^2 e^{2 j \phi}} } \\
t^{\textrm{TE}} &= \frac{ t_{12} t_{21} e^{j\phi}}{1 – r_{21}^2 e^{2 j \phi}}.
\end{aligned}
\end{equation}
It’s possible to produce a matched condition for which \( r_{12} = r_{21} = 0 \), by selecting
\begin{equation}\label{eqn:twoInterfaceNormal:240}
\begin{aligned}
0
&= \mu_2 k_{1z} – \mu_1 k_{2z} \\
&= \mu_1 \mu_2 \lr{ \inv{\mu_1} k_{1z} – \inv{\mu_2} k_{2z} } \\
&= \mu_1 \mu_2 \omega \lr{ \frac{1}{v_1 \mu_1} \theta_1 – \frac{1}{v_2 \mu_2} \theta_2 },
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:twoInterfaceNormal:260}
\inv{\eta_1} \cos\theta_1 = \inv{\eta_2} \cos\theta_2,
\end{equation}
so the matching condition for normal incidence is just
\begin{equation}\label{eqn:twoInterfaceNormal:280}
\eta_1 = \eta_2.
\end{equation}
Given this matched condition, the transmission coefficient for the 1,2 interface is
\begin{equation}\label{eqn:twoInterfaceNormal:300}
\begin{aligned}
t_{12}
&= \frac{2 \mu_2 k_{1z}}{\mu_2 k_{1z} + \mu_1 k_{2z}} \\
&= \frac{2 \mu_2 k_{1z}}{2 \mu_2 k_{1z} } \\
&= 1,
\end{aligned}
\end{equation}
so the matching condition yields
\begin{equation}\label{eqn:twoInterfaceNormal:320}
\begin{aligned}
t
&=
t_{12} t_{21} e^{j\phi} \\
&=
e^{j\phi} \\
&=
e^{-j k_2 d}.
\end{aligned}
\end{equation}
Normal transmission through a matched slab only introduces a phase delay.