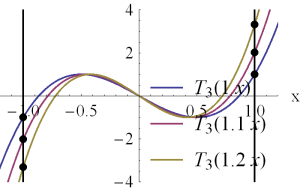[Click here for a PDF of this post with nicer formatting]
In our text [1] is a design procedure that applies Chebychev polynomials to the selection of current magnitudes for an evenly spaced array of identical antennas placed along the z-axis.
For an even number \( 2 M \) of identical antennas placed at positions \( \Br_m = (d/2) \lr{2 m -1} \Be_3 \), the array factor is
\begin{equation}\label{eqn:chebychevDesign:20}
\textrm{AF}
=
\sum_{m=-N}^N I_m e^{-j k \rcap \cdot \Br_m }.
\end{equation}
Assuming the currents are symmetric \( I_{-m} = I_m \), with \( \rcap = (\sin\theta \cos\phi, \sin\theta \sin\phi, \cos\theta ) \), and \( u = \frac{\pi d}{\lambda} \cos\theta \), this is
\begin{equation}\label{eqn:chebychevDesign:40}
\begin{aligned}
\textrm{AF}
&=
\sum_{m=-N}^N I_m e^{-j k (d/2) ( 2 m -1 )\cos\theta } \\
&=
2 \sum_{m=1}^N I_m \cos\lr{ k (d/2) ( 2 m -1)\cos\theta } \\
&=
2 \sum_{m=1}^N I_m \cos\lr{ (2 m -1) u }.
\end{aligned}
\end{equation}
This is a sum of only odd cosines, and can be expanded as a sum that includes all the odd powers of \( \cos u \). Suppose for example that this is a four element array with \( N = 2 \). In this case the array factor has the form
\begin{equation}\label{eqn:chebychevDesign:60}
\begin{aligned}
\textrm{AF}
&=
2 \lr{ I_1 \cos u + I_2 \lr{ 4 \cos^3 u – 3 \cos u } } \\
&=
2 \lr{ \lr{ I_1 – 3 I_2 } \cos u + 4 I_2 \cos^3 u }.
\end{aligned}
\end{equation}
The design procedure in the text sets \( \cos u = z/z_0 \), and then equates this to \( T_3(z) = 4 z^3 – 3 z \) to determine the current amplitudes \( I_m \). That is
\begin{equation}\label{eqn:chebychevDesign:80}
\frac{ 2 I_1 – 6 I_2 }{z_0} z + \frac{8 I_2}{z_0^3} z^3 = -3 z + 4 z^3,
\end{equation}
or
\begin{equation}\label{eqn:chebychevDesign:100}
\begin{aligned}
\begin{bmatrix}
I_1 \\
I_2
\end{bmatrix}
&=
{\begin{bmatrix}
2/z_0 & -6/z_0 \\
0 & 8/z_0^3
\end{bmatrix}}^{-1}
\begin{bmatrix}
-3 \\
4
\end{bmatrix} \\
&=
\frac{z_0}{2}
\begin{bmatrix}
3 (z_0^2 -1) \\
z_0^2
\end{bmatrix}.
\end{aligned}
\end{equation}
The currents in the array factor are fully determined up to a scale factor, reducing the array factor to
\begin{equation}\label{eqn:chebychevDesign:140}
\textrm{AF} = 4 z_0^3 \cos^3 u – 3 z_0 \cos u.
\end{equation}
The zeros of this array factor are located at the zeros of
\begin{equation}\label{eqn:chebychevDesign:120}
T_3( z_0 \cos u ) = \cos( 3 \cos^{-1} \lr{ z_0 \cos u } ),
\end{equation}
which are at \( 3 \cos^{-1} \lr{ z_0 \cos u } = \pi/2 + m \pi = \pi \lr{ m + \inv{2} } \)
\begin{equation}\label{eqn:chebychevDesign:160}
\cos u = \inv{z_0} \cos\lr{ \frac{\pi}{3} \lr{ m + \inv{2} } } = \setlr{ 0, \pm \frac{\sqrt{3}}{2 z_0} }.
\end{equation}
showing that the scaling factor \( z_0 \) effects the locations of the zeros. It also allows the values at the extremes \( \cos u = \pm 1 \), to increase past the \( \pm 1 \) non-scaled limit values. These effects can be explored in this Mathematica notebook, but can also be seen in fig. 1.
fig 1. T_3( z_0 x) for a few different scale factors z_0.
The scale factor can be fixed for a desired maximum power gain. For \( R
\textrm{dB} \), that will be when
\begin{equation}\label{eqn:chebychevDesign:180}
20 \log_{10} \cosh( 3 \cosh^{-1} z_0 ) = R \textrm{dB},
\end{equation}
or
\begin{equation}\label{eqn:chebychevDesign:200}
z_0 = \cosh \lr{ \inv{3} \cosh^{-1} \lr{ 10^{\frac{R}{20}} } }.
\end{equation}
For \( R = 30 \) dB (say), we have \( z_0 = 2.1 \), and
\begin{equation}\label{eqn:chebychevDesign:220}
\textrm{AF}
= 40 \cos^3 \lr{ \frac{\pi d}{\lambda} \cos\theta } – 6.4 \cos \lr{ \frac{\pi d}{\lambda} \cos\theta }.
\end{equation}
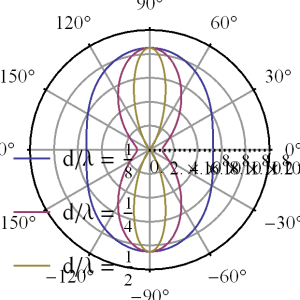
These are plotted in fig. 2 (linear scale), and fig. 3 (dB scale) for a couple values of \( d/\lambda \).
fig 2. T_3 fitting of 4 element array (linear scale).
fig 3. T_3 fitting of 4 element array (dB scale).
To explore the \( d/\lambda \) dependence try this Mathematica notebook.
References
[1] Constantine A Balanis. Antenna theory: analysis and design. John
Wiley & Sons, 3rd edition, 2005.
