Month: October 2020

Some nice positive feedback for my book.

October 31, 2020 math and physics play No comments , , , , , , , , , ,

Here’s a fun congratulatory email that I received today for my Geometric Algebra for Electrical Engineers book

Peeter ..
I had to email to congratulate you on your geometric algebra book. Like yourself, when I came across it, I was totally blown away and your book, being written from the position of a discoverer rather than an expert, answers most of the questions I was confronted by when reading Doran and Lasenby’s book.
You’re a C++ programmer and from my perspective, when using natural world math, you are constructing a representation of a problem (like code does) except many physicists do not recognize this. They’re doing physics with COBOL (or C with classes!).
congratulations
.. Reader
I couldn’t resist pointing out the irony of his COBOL comment, as my work at LzLabs is now heavily focused on COBOL (and PL/I) compilers and compiler runtimes.  You could say that my work, at work or at play, is all an attempt to transition people away from the evils of legacy COBOL.
For reference the Doran and Lasenby book is phenomenal work, but it is really hard material.  To attempt to read this, you’ll need a thorough understanding of electromagnetism, relativity, tensor algebra, quantum mechanics, advanced classical mechanics, and field theory.  I’m still working on this book, and it’s probably been 12 years since I bought it.  I managed to teach myself some of this material as I went, but also took most of the 4th year UofT undergrad physics courses (and some grad courses) to fill in some of the gaps.
When I titled my book, I included “for Electrical Engineers” in the title.  That titling choice was somewhat derivative, as there were already geometric algebra books “for physicists”,  and “for computer science“.  However, I thought it was also good shorthand for the prerequisites required for the book as “for Electrical Engineers” seemed to be good shorthand for “for a student that has seen electromagnetism in its div, grad, curl form, and doesn’t know special relativity, field theory, differential forms, tensor algebra, or other topics from more advanced physics.”
The relativistic presentation of electromagnetism in Doran and Lasenby, using the Dirac algebra (aka Space Time Algebra (STA)), is much more beautiful than the form that I have used in my book.  However, I was hoping to present the subject in a way that was accessible, and provided a stepping stone for the STA approach when the reader was ready to tackle a next interval of the “learning curve.”

Editing a book by tearing out pages!

October 25, 2020 Uncategorized No comments ,

I’ve been editing my classical mechanics notes compilation, which doesn’t yet justify being called a book.  Here’s the editing process in action:

I’ve purged about 120 pages, and wrote 16 new pages (covariant Lagrangian and Lorentz force material) to replace portions of some of the gutted material.  The stack beside the book is about 3/8″ thick of ripped out pages.  I ripped them out so that I could see the remainder more easily.

There’s still a lot to purge and rewrite, but I’m now down to a more manageable 347 pages, which is a good start.  Next up will be the material related to Lagrangian densities for field equations (wave equations, Maxwell’s equation, …)

Lagrangian for the Lorentz force equation.

October 24, 2020 math and physics play No comments , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,

[Click here for a PDF of this post with nicer formatting]

Motivation.

In my old classical mechanics notes it appears that I did covariant derivations of the Lorentz force equations a number of times, using different trial Lagrangians (relativistic and non-relativistic), and using both geometric algebra and tensor methods. However, none of these appear to have been done concisely, and a number not even coherently.

The following document has been drafted as replacement text for those incoherent classical mechanics notes. I’ll attempt to cover

  • a lighting review of the geometric algebra STA (Space Time Algebra),
  • relations between Dirac matrix algebra and STA,
  • derivation of the relativistic form of the Euler-Lagrange equations from the covariant form of the action,
  • relationship of the STA form of the Euler-Lagrange equations to their tensor equivalents,
  • derivation of the Lorentz force equation from the STA Lorentz force Lagrangian,
  • relationship of the STA Lorentz force equation to its equivalent in the tensor formalism,
  • relationship of the STA Lorentz force equation to the traditional vector form.

Note that some of the prerequisite ideas and auxiliary details are presented as problems with solutions. If the reader has sufficient background to attempt those problems themselves, they are encouraged to do so.

The STA and geometric algebra ideas used here are not complete to learn from in isolation. The reader is referred to [1] for a more complete exposition of both STA and geometric algebra.

Conventions.

Definition 1.1: Index conventions.

Latin indexes \( i, j, k, r, s, t, \cdots \) are used to designate values in the range \( \setlr{ 1,2,3 } \). Greek indexes are \( \alpha, \beta, \mu, \nu, \cdots \) are used for indexes of spacetime quantities \( \setlr{0,1,2,3} \).
The Einstein convention of implied summation for mixed upper and lower Greek indexes will be used, for example
\begin{equation*}
x^\alpha x_\alpha \equiv \sum_{\alpha = 0}^3 x^\alpha x_\alpha.
\end{equation*}

Space Time Algebra (STA.)

In the geometric algebra literature, the Dirac algebra of quantum field theory has been rebranded Space Time Algebra (STA). The differences between STA and the Dirac theory that uses matrices (\( \gamma_\mu \)) are as follows

  • STA completely omits any representation of the Dirac basis vectors \( \gamma_\mu \). In particular, any possible matrix representation is irrelevant.
  • STA provides a rich set of fundamental operations (grade selection, generalized dot and wedge products for multivector elements, rotation and reflection operations, …)
  • Matrix trace, and commutator and anticommutator operations are nowhere to be found in STA, as geometrically grounded equivalents are available instead.
  • The “slashed” quantities from Dirac theory, such as \( \gamma_\mu p^\mu \) are nothing more than vectors in their entirety in STA (where the basis is no longer implicit, as is the case for coordinates.)

Our basis vectors have the following properties.

Definition 1.2: Standard basis.

Let the four-vector standard basis be designated \( \setlr{\gamma_0, \gamma_1, \gamma_2, \gamma_3 } \), where the basis vectors satisfy
\begin{equation}\label{eqn:lorentzForceCovariant:1540}
\begin{aligned}
\gamma_0^2 &= -\gamma_i^2 = 1 \\
\gamma_\alpha \cdot \gamma_\beta &= 0, \forall \alpha \ne \beta.
\end{aligned}
\end{equation}

Problem: Commutator properties of the STA basis.

In Dirac theory, the commutator properties of the Dirac matrices is considered fundamental, namely
\begin{equation*}
\symmetric{\gamma_\mu}{\gamma_\nu} = 2 \eta_{\mu\nu}.
\end{equation*}

Show that this follows from the axiomatic assumptions of geometric algebra, and describe how the dot and wedge products are related to the anticommutator and commutator products of Dirac theory.

Answer

The anticommutator is defined as symmetric sum of products
\begin{equation}\label{eqn:lorentzForceCovariant:1040}
\symmetric{\gamma_\mu}{\gamma_\nu}
\equiv
\gamma_\mu \gamma_\nu
+
\gamma_\nu \gamma_\mu,
\end{equation}
but this is just twice the dot product in its geometric algebra form \( a b = (a b + ba)/2 \). Observe that the properties of the basis vectors defined in \ref{eqn:lorentzForceCovariant:1540} may be summarized as
\begin{equation}\label{eqn:lorentzForceCovariant:1060}
\gamma_\mu \cdot \gamma_\nu = \eta_{\mu\nu},
\end{equation}
where \( \eta_{\mu\nu} = \text{diag}(+,-,-,-)
=
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & -1 & 0 & 0 \\
0 & 0 & -1 & 0 \\
0 & 0 & 0 & -1 \\
\end{bmatrix}
\) is the conventional metric tensor. This means
\begin{equation}\label{eqn:lorentzForceCovariant:1080}
\gamma_\mu \cdot \gamma_\nu = \eta_{\mu\nu} = 2 \symmetric{\gamma_\mu}{\gamma_\nu},
\end{equation}
as claimed.

Similarly, observe that the commutator, defined as the antisymmetric sum of products
\begin{equation}\label{eqn:lorentzForceCovariant:1100}
\antisymmetric{\gamma_\mu}{\gamma_\nu} \equiv
\gamma_\mu \gamma_\nu
–
\gamma_\nu \gamma_\mu,
\end{equation}
is twice the wedge product \( a \wedge b = (a b – b a)/2 \). This provides geometric identifications for the respective anti-commutator and commutator products respectively
\begin{equation}\label{eqn:lorentzForceCovariant:1120}
\begin{aligned}
\symmetric{\gamma_\mu}{\gamma_\nu} &= 2 \gamma_\mu \cdot \gamma_\nu \\
\antisymmetric{\gamma_\mu}{\gamma_\nu} &= 2 \gamma_\mu \wedge \gamma_\nu,
\end{aligned}
\end{equation}

Definition 1.3: Pseudoscalar.

The pseudoscalar for the space is denoted \( I = \gamma_0 \gamma_1 \gamma_2 \gamma_3 \).

Problem: Pseudoscalar.

Show that the STA pseudoscalar \( I \) defined by \ref{eqn:lorentzForceCovariant:1540} satisfies
\begin{equation*}
\tilde{I} = I,
\end{equation*}
where the tilde operator designates reversion. Also show that \( I \) has the properties of an imaginary number
\begin{equation*}
I^2 = -1.
\end{equation*}
Finally, show that, unlike the spatial pseudoscalar that commutes with all grades, \( I \) anticommutes with any vector or trivector, and commutes with any bivector.

Answer

Since \( \gamma_\alpha \gamma_\beta = -\gamma_\beta \gamma_\alpha \) for any \( \alpha \ne \beta \), any permutation of the factors of \( I \) changes the sign once. In particular
\begin{equation}\label{eqn:lorentzForceCovariant:680}
\begin{aligned}
I &=
\gamma_0
\gamma_1
\gamma_2
\gamma_3 \\
&=
–
\gamma_1
\gamma_2
\gamma_3
\gamma_0 \\
&=
–
\gamma_2
\gamma_3
\gamma_1
\gamma_0 \\
&=
+
\gamma_3
\gamma_2
\gamma_1
\gamma_0
= \tilde{I}.
\end{aligned}
\end{equation}
Using this, we have
\begin{equation}\label{eqn:lorentzForceCovariant:700}
\begin{aligned}
I^2
&= I \tilde{I} \\
&=
(
\gamma_0
\gamma_1
\gamma_2
\gamma_3
)(
\gamma_3
\gamma_2
\gamma_1
\gamma_0
) \\
&=
\lr{\gamma_0}^2
\lr{\gamma_1}^2
\lr{\gamma_2}^2
\lr{\gamma_3}^2 \\
&=
(+1)
(-1)
(-1)
(-1) \\
&= -1.
\end{aligned}
\end{equation}
To illustrate the anticommutation property with any vector basis element, consider the following two examples:
\begin{equation}\label{eqn:lorentzForceCovariant:720}
\begin{aligned}
I \gamma_0 &=
\gamma_0
\gamma_1
\gamma_2
\gamma_3
\gamma_0 \\
&=
–
\gamma_0
\gamma_0
\gamma_1
\gamma_2
\gamma_3 \\
&=
–
\gamma_0 I,
\end{aligned}
\end{equation}
\begin{equation}\label{eqn:lorentzForceCovariant:740}
\begin{aligned}
I \gamma_2
&=
\gamma_0
\gamma_1
\gamma_2
\gamma_3
\gamma_2 \\
&=
–
\gamma_0
\gamma_1
\gamma_2
\gamma_2
\gamma_3 \\
&=
–
\gamma_2
\gamma_0
\gamma_1
\gamma_2
\gamma_3 \\
&= -\gamma_2 I.
\end{aligned}
\end{equation}
A total of three sign swaps is required to “percolate” any given \(\gamma_\alpha\) through the factors of \( I \), resulting in an overall sign change of \( -1 \).

For any bivector basis element \( \alpha \ne \beta \)
\begin{equation}\label{eqn:lorentzForceCovariant:760}
\begin{aligned}
I \gamma_\alpha \gamma_\beta
&=
-\gamma_\alpha I \gamma_\beta \\
&=
+\gamma_\alpha \gamma_\beta I.
\end{aligned}
\end{equation}

Similarly for any trivector basis element \( \alpha \ne \beta \ne \sigma \)
\begin{equation}\label{eqn:lorentzForceCovariant:780}
\begin{aligned}
I \gamma_\alpha \gamma_\beta \gamma_\sigma
&=
-\gamma_\alpha I \gamma_\beta \gamma_\sigma \\
&=
+\gamma_\alpha \gamma_\beta I \gamma_\sigma \\
&=
-\gamma_\alpha \gamma_\beta \gamma_\sigma I.
\end{aligned}
\end{equation}

Definition 1.4: Reciprocal basis.

The reciprocal basis \( \setlr{ \gamma^0, \gamma^1, \gamma^2, \gamma^3 } \) is defined , such that the property \( \gamma^\alpha \cdot \gamma_\beta = {\delta^\alpha}_\beta \) holds.

Observe that, \( \gamma^0 = \gamma_0 \) and \( \gamma^i = -\gamma_i \).

Theorem 1.1: Coordinates.

Coordinates are defined in terms of dot products with the standard basis, or reciprocal basis
\begin{equation*}
\begin{aligned}
x^\alpha &= x \cdot \gamma^\alpha \\
x_\alpha &= x \cdot \gamma_\alpha,
\end{aligned}
\end{equation*}

Start proof:

Suppose that a coordinate representation of the following form is assumed
\begin{equation}\label{eqn:lorentzForceCovariant:820}
x = x^\alpha \gamma_\alpha = x_\beta \gamma^\beta.
\end{equation}
We wish to determine the representation of the \( x^\alpha \) or \( x_\beta \) coordinates in terms of \( x\) and the basis elements. Taking the dot product with any standard basis element, we find
\begin{equation}\label{eqn:lorentzForceCovariant:840}
\begin{aligned}
x \cdot \gamma_\mu
&= (x_\beta \gamma^\beta) \cdot \gamma_\mu \\
&= x_\beta {\delta^\beta}_\mu \\
&= x_\mu,
\end{aligned}
\end{equation}
as claimed. Similarly, dotting with a reciprocal frame vector, we find
\begin{equation}\label{eqn:lorentzForceCovariant:860}
\begin{aligned}
x \cdot \gamma^\mu
&= (x^\beta \gamma_\beta) \cdot \gamma^\mu \\
&= x^\beta {\delta_\beta}^\mu \\
&= x^\mu.
\end{aligned}
\end{equation}

End proof.

Observe that raising or lowering the index of a spatial index toggles the sign of a coordinate, but timelike indexes are left unchanged.
\begin{equation}\label{eqn:lorentzForceCovariant:880}
\begin{aligned}
x^0 &= x_0 \\
x^i &= -x_i \\
\end{aligned}
\end{equation}

Definition 1.5: Spacetime gradient.

The spacetime gradient operator is
\begin{equation*}
\grad = \gamma^\mu \partial_\mu = \gamma_\nu \partial^\nu,
\end{equation*}
where
\begin{equation*}
\partial_\mu = \PD{x^\mu}{},
\end{equation*}
and
\begin{equation*}
\partial^\mu = \PD{x_\mu}{}.
\end{equation*}

This definition of gradient is consistent with the Dirac gradient (sometimes denoted as a slashed \(\partial\)).

Definition 1.6: Timelike and spacelike components of a four-vector.

Given a four vector \( x = \gamma_\mu x^\mu \), that would be designated \( x^\mu = \setlr{ x^0, \Bx} \) in conventional special relativity, we write
\begin{equation*}
x^0 = x \cdot \gamma_0,
\end{equation*}
and
\begin{equation*}
\Bx = x \wedge \gamma_0,
\end{equation*}
or
\begin{equation*}
x = (x^0 + \Bx) \gamma_0.
\end{equation*}

The spacetime split of a four-vector \( x \) is relative to the frame. In the relativistic lingo, one would say that it is “observer dependent”, as the same operations with \( {\gamma_0}’ \), the timelike basis vector for a different frame, would yield a different set of coordinates.

While the dot and wedge products above provide an effective mechanism to split a four vector into a set of timelike and spacelike quantities, the spatial component of a vector has a bivector representation in STA. Consider the following coordinate expansion of a spatial vector
\begin{equation}\label{eqn:lorentzForceCovariant:1000}
\Bx =
x \wedge \gamma_0
=
\lr{ x^\mu \gamma_\mu } \wedge \gamma_0
=
\sum_{k = 1}^3 x^k \gamma_k \gamma_0.
\end{equation}

Definition 1.7: Spatial basis.

We designate
\begin{equation}\label{eqn:lorentzForceCovariant:1560}
\Be_i = \gamma_i \gamma_0,
\end{equation}
as the standard basis vectors for \(\mathbb{R}^3\).

In the literature, this bivector representation of the spatial basis may be designated \( \sigma_i = \gamma_i \gamma_0 \), as these bivectors have the properties of the Pauli matrices \( \sigma_i \). Because I intend to expand these notes to include purely non-relativistic applications, I won’t use the Pauli notation here.

Problem: Orthonormality of the spatial basis.

Show that the spatial basis \( \setlr{ \Be_1, \Be_2, \Be_3 } \), defined by \ref{eqn:lorentzForceCovariant:1560}, is orthonormal.

Answer

\begin{equation}\label{eqn:lorentzForceCovariant:620}
\begin{aligned}
\Be_i \cdot \Be_j
&= \gpgradezero{ \gamma_i \gamma_0 \gamma_j \gamma_0 } \\
&= -\gpgradezero{ \gamma_i \gamma_j } \\
&= – \gamma_i \cdot \gamma_j.
\end{aligned}
\end{equation}
This is zero for all \( i \ne j \), and unity for any \( i = j \).

Problem: Spatial pseudoscalar.

Show that the STA pseudoscalar \( I = \gamma_0 \gamma_1 \gamma_2 \gamma_3 \) equals the spatial pseudoscalar \( I = \Be_1 \Be_2 \Be_3 \).

Answer

The spatial pseudoscalar, expanded in terms of the STA basis vectors, is
\begin{equation}\label{eqn:lorentzForceCovariant:1020}
\begin{aligned}
I
&= \Be_1 \Be_2 \Be_3 \\
&= \lr{ \gamma_1 \gamma_0 }
\lr{ \gamma_2 \gamma_0 }
\lr{ \gamma_3 \gamma_0 } \\
&= \lr{ \gamma_1 \gamma_0 } \gamma_2 \lr{ \gamma_0 \gamma_3 } \gamma_0 \\
&= \lr{ -\gamma_0 \gamma_1 } \gamma_2 \lr{ -\gamma_3 \gamma_0 } \gamma_0 \\
&= \gamma_0 \gamma_1 \gamma_2 \gamma_3 \lr{ \gamma_0 \gamma_0 } \\
&= \gamma_0 \gamma_1 \gamma_2 \gamma_3,
\end{aligned}
\end{equation}
as claimed.

Problem: Characteristics of the Pauli matrices.

The Pauli matrices obey the following anticommutation relations:
\begin{equation}\label{eqn:lorentzForceCovariant:660}
\symmetric{ \sigma_a}{\sigma_b } = 2 \delta_{a b},
\end{equation}
and commutation relations:
\begin{equation}\label{eqn:lorentzForceCovariant:640}
\antisymmetric{ \sigma_a}{ \sigma_b } = 2 i \epsilon_{a b c}\,\sigma_c,
\end{equation}
Show how these relate to the geometric algebra dot and wedge products, and determine the geometric algebra representation of the imaginary \( i \) above.

Euler-Lagrange equations.

I’ll start at ground zero, with the derivation of the relativistic form of the Euler-Lagrange equations from the action. A relativistic action for a single particle system has the form
\begin{equation}\label{eqn:lorentzForceCovariant:20}
S = \int d\tau L(x, \dot{x}),
\end{equation}
where \( x \) is the spacetime coordinate, \( \dot{x} = dx/d\tau \) is the four-velocity, and \( \tau \) is proper time.

Theorem 1.2: Relativistic Euler-Lagrange equations.

Let \( x \rightarrow x + \delta x \) be any variation of the Lagrangian four-vector coordinates, where \( \delta x = 0 \) at the boundaries of the action integral. The variation of the action is
\begin{equation}\label{eqn:lorentzForceCovariant:1580}
\delta S = \int d\tau \delta x \cdot \delta L(x, \dot{x}),
\end{equation}
where
\begin{equation}\label{eqn:lorentzForceCovariant:1600}
\delta L = \grad L – \frac{d}{d\tau} (\grad_v L),
\end{equation}
where \( \grad = \gamma^\mu \partial_\mu \), and where we construct a similar velocity-gradient with respect to the proper-time derivatives of the coordinates \( \grad_v = \gamma^\mu \partial/\partial \dot{x}^\mu \).The action is extremized when \( \delta S = 0 \), or when \( \delta L = 0 \). This latter condition is called the Euler-Lagrange equations.

Start proof:

Let \( \epsilon = \delta x \), and expand the Lagrangian in Taylor series to first order
\begin{equation}\label{eqn:lorentzForceCovariant:60}
\begin{aligned}
S &\rightarrow S + \delta S \\
&= \int d\tau L( x + \epsilon, \dot{x} + \dot{\epsilon})
&=
\int d\tau \lr{
L(x, \dot{x}) + \epsilon \cdot \grad L + \dot{\epsilon} \cdot \grad_v L
}.
\end{aligned}
\end{equation}
Subtracting off \( S \) and integrating by parts, leaves
\begin{equation}\label{eqn:lorentzForceCovariant:80}
\delta S =
\int d\tau \epsilon \cdot \lr{
\grad L – \frac{d}{d\tau} \grad_v L
}
+
\int d\tau \frac{d}{d\tau} (\grad_v L ) \cdot \epsilon.
\end{equation}
The boundary integral
\begin{equation}\label{eqn:lorentzForceCovariant:100}
\int d\tau \frac{d}{d\tau} (\grad_v L ) \cdot \epsilon
=
\evalbar{(\grad_v L ) \cdot \epsilon}{\Delta \tau} = 0,
\end{equation}
is zero since the variation \( \epsilon \) is required to vanish on the boundaries. So, if \( \delta S = 0 \), we must have
\begin{equation}\label{eqn:lorentzForceCovariant:120}
0 =
\int d\tau \epsilon \cdot \lr{
\grad L – \frac{d}{d\tau} \grad_v L
},
\end{equation}
for all variations \( \epsilon \). Clearly, this requires that
\begin{equation}\label{eqn:lorentzForceCovariant:140}
\delta L = \grad L – \frac{d}{d\tau} (\grad_v L) = 0,
\end{equation}
or
\begin{equation}\label{eqn:lorentzForceCovariant:145}
\grad L = \frac{d}{d\tau} (\grad_v L),
\end{equation}
which is the coordinate free statement of the Euler-Lagrange equations.

End proof.

Problem: Coordinate form of the Euler-Lagrange equations.

Working in coordinates, use the action argument show that the Euler-Lagrange equations have the form
\begin{equation*}
\PD{x^\mu}{L} = \frac{d}{d\tau} \PD{\dot{x}^\mu}{L}
\end{equation*}
Observe that this is identical to the statement of \ref{eqn:lorentzForceCovariant:1600} after contraction with \( \gamma^\mu \).

Answer

In terms of coordinates, the first order Taylor expansion of the action is
\begin{equation}\label{eqn:lorentzForceCovariant:180}
\begin{aligned}
S &\rightarrow S + \delta S \\
&= \int d\tau L( x^\alpha + \epsilon^\alpha, \dot{x}^\alpha + \dot{\epsilon}^\alpha) \\
&=
\int d\tau \lr{
L(x^\alpha, \dot{x}^\alpha) + \epsilon^\mu \PD{x^\mu}{L} + \dot{\epsilon}^\mu \PD{\dot{x}^\mu}{L}
}.
\end{aligned}
\end{equation}
As before, we integrate by parts to separate out a pure boundary term
\begin{equation}\label{eqn:lorentzForceCovariant:200}
\delta S =
\int d\tau \epsilon^\mu
\lr{
\PD{x^\mu}{L} – \frac{d}{d\tau} \PD{\dot{x}^\mu}{L}
}
+
\int d\tau \frac{d}{d\tau} \lr{
\epsilon^\mu \PD{\dot{x}^\mu}{L}
}.
\end{equation}
The boundary term is killed since \( \epsilon^\mu = 0 \) at the end points of the action integral. We conclude that extremization of the action (\( \delta S = 0 \), for all \( \epsilon^\mu \)) requires
\begin{equation}\label{eqn:lorentzForceCovariant:220}
\PD{x^\mu}{L} – \frac{d}{d\tau} \PD{\dot{x}^\mu}{L} = 0.
\end{equation}

Lorentz force equation.

Theorem 1.3: Lorentz force.

The relativistic Lagrangian for a charged particle is
\begin{equation}\label{eqn:lorentzForceCovariant:1640}
L = \inv{2} m v^2 + q A \cdot v/c.
\end{equation}
Application of the Euler-Lagrange equations to this Lagrangian yields the Lorentz-force equation
\begin{equation}\label{eqn:lorentzForceCovariant:1660}
\frac{dp}{d\tau} = q F \cdot v/c,
\end{equation}
where \( p = m v \) is the proper momentum, \( F \) is the Faraday bivector \( F = \grad \wedge A \), and \( c \) is the speed of light.

Start proof:

To make life easier, let’s take advantage of the linearity of the Lagrangian, and break it into the free particle Lagrangian \( L_0 = (1/2) m v^2 \) and a potential term \( L_1 = q A \cdot v/c \). For the free particle case we have
\begin{equation}\label{eqn:lorentzForceCovariant:240}
\begin{aligned}
\delta L_0
&= \grad L_0 – \frac{d}{d\tau} (\grad_v L_0) \\
&= – \frac{d}{d\tau} (m v) \\
&= – \frac{dp}{d\tau}.
\end{aligned}
\end{equation}
For the potential contribution we have
\begin{equation}\label{eqn:lorentzForceCovariant:260}
\begin{aligned}
\delta L_1
&= \grad L_1 – \frac{d}{d\tau} (\grad_v L_1) \\
&= \frac{q}{c} \lr{ \grad (A \cdot v) – \frac{d}{d\tau} \lr{ \grad_v (A \cdot v)} } \\
&= \frac{q}{c} \lr{ \grad (A \cdot v) – \frac{dA}{d\tau} }.
\end{aligned}
\end{equation}
The proper time derivative can be evaluated using the chain rule
\begin{equation}\label{eqn:lorentzForceCovariant:280}
\frac{dA}{d\tau}
=
\frac{\partial x^\mu}{\partial \tau} \partial_\mu A
= (v \cdot \grad) A.
\end{equation}
Putting all the pieces back together we have
\begin{equation}\label{eqn:lorentzForceCovariant:300}
\begin{aligned}
0
&= \delta L \\
&=
-\frac{dp}{d\tau} + \frac{q}{c} \lr{ \grad (A \cdot v) – (v \cdot \grad) A } \\
&=
-\frac{dp}{d\tau} + \frac{q}{c} \lr{ \grad \wedge A } \cdot v.
\end{aligned}
\end{equation}

End proof.

Problem: Gradient of a squared position vector.

Show that
\begin{equation*}
\grad (a \cdot x) = a,
\end{equation*}
and
\begin{equation*}
\grad x^2 = 2 x.
\end{equation*}
It should be clear that the same ideas can be used for the velocity gradient, where we obtain \( \grad_v (v^2) = 2 v \), and \( \grad_v (A \cdot v) = A \), as used in the derivation above.

Answer

The first identity follows easily by expansion in coordinates
\begin{equation}\label{eqn:lorentzForceCovariant:320}
\begin{aligned}
\grad (a \cdot x)
&=
\gamma^\mu \partial_\mu a_\alpha x^\alpha \\
&=
\gamma^\mu a_\alpha \delta_\mu^\alpha \\
&=
\gamma^\mu a_\mu \\
&=
a.
\end{aligned}
\end{equation}
The second identity follows by linearity of the gradient
\begin{equation}\label{eqn:lorentzForceCovariant:340}
\begin{aligned}
\grad x^2
&=
\grad (x \cdot x) \\
&=
\evalbar{\lr{\grad (x \cdot a)}}{a = x}
+
\evalbar{\lr{\grad (b \cdot x)}}{b = x} \\
&=
\evalbar{a}{a = x}
+
\evalbar{b}{b = x} \\
&=
2x.
\end{aligned}
\end{equation}

It is desirable to put this relativistic Lorentz force equation into the usual vector and tensor forms for comparison.

Theorem 1.4: Tensor form of the Lorentz force equation.

The tensor form of the Lorentz force equation is
\begin{equation}\label{eqn:lorentzForceCovariant:1620}
\frac{dp^\mu}{d\tau} = \frac{q}{c} F^{\mu\nu} v_\nu,
\end{equation}
where the antisymmetric Faraday tensor is defined as \( F^{\mu\nu} = \partial^\mu A^\nu – \partial^\nu A^\mu \).

Start proof:

We have only to dot both sides with \( \gamma^\mu \). On the left we have
\begin{equation}\label{eqn:lorentzForceCovariant:380}
\gamma^\mu \cdot \frac{dp}{d\tau}
=
\frac{dp^\mu}{d\tau}.
\end{equation}
On the right, we have
\begin{equation}\label{eqn:lorentzForceCovariant:400}
\begin{aligned}
\gamma^\mu \cdot \lr{ \frac{q}{c} F \cdot v }
&=
\frac{q}{c} (( \grad \wedge A ) \cdot v ) \cdot \gamma^\mu \\
&=
\frac{q}{c} ( \grad ( A \cdot v ) – (v \cdot \grad) A ) \cdot \gamma^\mu \\
&=
\frac{q}{c} \lr{ (\partial^\mu A^\nu) v_\nu – v_\nu \partial^\nu A^\mu } \\
&=
\frac{q}{c} F^{\mu\nu} v_\nu.
\end{aligned}
\end{equation}

End proof.

Problem: Tensor expansion of \(F\).

An alternate way to demonstrate \ref{eqn:lorentzForceCovariant:1620} is to first expand \( F = \grad \wedge A \) in terms of coordinates, an expansion that can be expressed in terms of a second rank tensor antisymmetric tensor \( F^{\mu\nu} \). Find that expansion, and re-evaluate the dot products of \ref{eqn:lorentzForceCovariant:400} using that.

Answer

\begin{equation}\label{eqn:lorentzForceCovariant:900}
\begin{aligned}
F &=
\grad \wedge A \\
&=
\lr{ \gamma_\mu \partial^\mu } \wedge \lr{ \gamma_\nu A^\nu } \\
&=
\lr{ \gamma_\mu \wedge \gamma_\nu } \partial^\mu A^\nu.
\end{aligned}
\end{equation}
To this we can use the usual tensor trick (add self to self, change indexes, and divide by two), to give
\begin{equation}\label{eqn:lorentzForceCovariant:920}
\begin{aligned}
F &=
\inv{2} \lr{
\lr{ \gamma_\mu \wedge \gamma_\nu } \partial^\mu A^\nu
+
\lr{ \gamma_\nu \wedge \gamma_\mu } \partial^\nu A^\mu
} \\
&=
\inv{2}
\lr{ \gamma_\mu \wedge \gamma_\nu } \lr{
\partial^\mu A^\nu
–
\partial^\nu A^\mu
},
\end{aligned}
\end{equation}
which is just
\begin{equation}\label{eqn:lorentzForceCovariant:940}
F =
\inv{2} \lr{ \gamma_\mu \wedge \gamma_\nu } F^{\mu\nu}.
\end{equation}
Now, let’s expand \( (F \cdot v) \cdot \gamma^\mu \) to compare to the earlier expansion in terms of \( \grad \) and \( A \).
\begin{equation}\label{eqn:lorentzForceCovariant:960}
\begin{aligned}
(F \cdot v) \cdot \gamma^\mu
&=
\inv{2}
F^{\alpha\nu}
\lr{ \lr{ \gamma_\alpha \wedge \gamma_\nu } \cdot \lr{ \gamma^\beta v_\beta } } \cdot \gamma^\mu \\
&=
\inv{2}
F^{\alpha\nu} v_\beta
\lr{
{\delta_\nu}^\beta {\gamma_\alpha}^\mu
–
{\delta_\alpha}^\beta {\gamma_\nu}^\mu
} \\
&=
\inv{2}
\lr{
F^{\mu\beta} v_\beta
–
F^{\beta\mu} v_\beta
} \\
&=
F^{\mu\nu} v_\nu.
\end{aligned}
\end{equation}
This alternate expansion illustrates some of the connectivity between the geometric algebra approach and the traditional tensor formalism.

Problem: Lorentz force direct tensor derivation.

Instead of using the geometric algebra form of the Lorentz force equation as a stepping stone, we may derive the tensor form from the Lagrangian directly, provided the Lagrangian is put into tensor form
\begin{equation*}
L = \inv{2} m v^\mu v_\mu + q A^\mu v_\mu /c.
\end{equation*}
Evaluate the Euler-Lagrange equations in coordinate form and compare to \ref{eqn:lorentzForceCovariant:1620}.

Answer

Let \( \delta_\mu L = \gamma_\mu \cdot \delta L \), so that we can write the Euler-Lagrange equations as
\begin{equation}\label{eqn:lorentzForceCovariant:460}
0 = \delta_\mu L = \PD{x^\mu}{L} – \frac{d}{d\tau} \PD{\dot{x}^\mu}{L}.
\end{equation}
Operating on the kinetic term of the Lagrangian, we have
\begin{equation}\label{eqn:lorentzForceCovariant:480}
\delta_\mu L_0 = – \frac{d}{d\tau} m v_\mu.
\end{equation}
For the potential term
\begin{equation}\label{eqn:lorentzForceCovariant:500}
\begin{aligned}
\delta_\mu L_1
&=
\frac{q}{c} \lr{
v_\nu \PD{x^\mu}{A^\nu} – \frac{d}{d\tau} A_\mu
} \\
&=
\frac{q}{c} \lr{
v_\nu \PD{x^\mu}{A^\nu} – \frac{dx_\alpha}{d\tau} \PD{x_\alpha}{ A_\mu }
} \\
&=
\frac{q}{c} v^\nu \lr{
\partial_\mu A_\nu – \partial_\nu A_\mu
} \\
&=
\frac{q}{c} v^\nu F_{\mu\nu}.
\end{aligned}
\end{equation}
Putting the pieces together gives
\begin{equation}\label{eqn:lorentzForceCovariant:520}
\frac{d}{d\tau} (m v_\mu) = \frac{q}{c} v^\nu F_{\mu\nu},
\end{equation}
which is identical\footnote{Some minor index raising and lowering gymnastics are required.} to the tensor form that we found by expanding the geometric algebra form of Maxwell’s equation in coordinates.

Theorem 1.5: Vector Lorentz force equation.

Relative to a fixed observer’s frame, the Lorentz force equation of \ref{eqn:lorentzForceCovariant:1660} splits into a spatial rate of change of momentum, and (timelike component) rate of change of energy, as follows
\begin{equation}\label{eqn:lorentzForceCovariant:1680}
\begin{aligned}
\ddt{(\gamma m \Bv)} &= q \lr{ \BE + \Bv \cross \BB } \\
\ddt{(\gamma m c^2)} &= q \Bv \cdot \BE,
\end{aligned}
\end{equation}
where \( F = \BE + I c \BB \), \( \gamma = 1/\sqrt{1 – \Bv^2/c^2 }\).

Start proof:

The first step is to eliminate the proper time dependencies in the Lorentz force equation. Consider first the coordinate representation of an arbitrary position four-vector \( x \)
\begin{equation}\label{eqn:lorentzForceCovariant:1140}
x = c t \gamma_0 + x^k \gamma_k.
\end{equation}
The corresponding four-vector velocity is
\begin{equation}\label{eqn:lorentzForceCovariant:1160}
v = \ddtau{x} = c \ddtau{t} \gamma_0 + \ddtau{t} \ddt{x^k} \gamma_k.
\end{equation}
By construction, \( v^2 = c^2 \) is a Lorentz invariant quantity (this is one of the relativistic postulates), so the LHS of \ref{eqn:lorentzForceCovariant:1160} must have the same square. That is
\begin{equation}\label{eqn:lorentzForceCovariant:1240}
c^2 = \lr{ \ddtau{t} }^2 \lr{ c^2 – \Bv^2 },
\end{equation}
where \( \Bv = v \wedge \gamma_0 \). This shows that we may make the identification
\begin{equation}\label{eqn:lorentzForceCovariant:1260}
\gamma = \ddtau{t} = \inv{1 – \Bv^2/c^2 },
\end{equation}
and
\begin{equation}\label{eqn:lorentzForceCovariant:1280}
\ddtau{} = \ddtau{t} \ddt{} = \gamma \ddt{}.
\end{equation}
We may now factor the four-velocity \( v \) into its spacetime split
\begin{equation}\label{eqn:lorentzForceCovariant:1300}
v = \gamma \lr{ c + \Bv } \gamma_0.
\end{equation}
In particular the LHS of the Lorentz force equation can be rewritten as
\begin{equation}\label{eqn:lorentzForceCovariant:1320}
\ddtau{p} = \gamma \ddt{}\lr{ \gamma \lr{ c + \Bv } } \gamma_0,
\end{equation}
and the RHS of the Lorentz force equation can be rewritten as
\begin{equation}\label{eqn:lorentzForceCovariant:1340}
\frac{q}{c} F \cdot v
=
\frac{\gamma q}{c} F \cdot \lr{ (c + \Bv) \gamma_0 }.
\end{equation}
Equating timelike and spacelike components leaves us
\begin{equation}\label{eqn:lorentzForceCovariant:1380}
\ddt{ (m \gamma c) } = \frac{q}{c} \lr{ F \cdot \lr{ (c + \Bv) \gamma_0 } } \cdot \gamma_0,
\end{equation}
\begin{equation}\label{eqn:lorentzForceCovariant:1400}
\ddt{ (m \gamma \Bv) } = \frac{q}{c} \lr{ F \cdot \lr{ (c + \Bv) \gamma_0 } } \wedge \gamma_0,
\end{equation}
Evaluating these products requires some care, but is an essentially manual process. The reader is encouraged to do so once, but the end result may also be obtained easily using software (see lorentzForce.nb in [2]). One finds
\begin{equation}\label{eqn:lorentzForceCovariant:1440}
F = \BE + I c \BB
=
E^1 \gamma_{10} +
+ E^2 \gamma_{20} +
+ E^3 \gamma_{30} +
– c B^1 \gamma_{23} +
– c B^2 \gamma_{31} +
– c B^3 \gamma_{12},
\end{equation}
\begin{equation}\label{eqn:lorentzForceCovariant:1460}
\frac{q}{c} \lr{ F \cdot \lr{ (c + \Bv) \gamma_0 } } \cdot \gamma_0
= \frac{q}{c} \BE \cdot \Bv,
\end{equation}
\begin{equation}\label{eqn:lorentzForceCovariant:1480}
\frac{q}{c} \lr{ F \cdot \lr{ (c + \Bv) \gamma_0 } } \wedge \gamma_0
= q \lr{ \BE + \Bv \cross \BB }.
\end{equation}

End proof.

Problem: Algebraic spacetime split of the Lorentz force equation.

Derive the results of \ref{eqn:lorentzForceCovariant:1440} through \ref{eqn:lorentzForceCovariant:1480} algebraically.

Problem: Spacetime split of the Lorentz force tensor equation.

Show that \ref{eqn:lorentzForceCovariant:1680} also follows from the tensor form of the Lorentz force equation (\ref{eqn:lorentzForceCovariant:1620}) provided we identify
\begin{equation}\label{eqn:lorentzForceCovariant:1500}
F^{k0} = E^k,
\end{equation}
and
\begin{equation}\label{eqn:lorentzForceCovariant:1520}
F^{rs} = -\epsilon^{rst} B^t.
\end{equation}

Also verify that the identifications of \ref{eqn:lorentzForceCovariant:1500} and \ref{eqn:lorentzForceCovariant:1520} is consistent with the geometric algebra Faraday bivector \( F = \BE + I c \BB \), and the associated coordinate expansion of the field \( F = (1/2) (\gamma_\mu \wedge \gamma_\nu) F^{\mu\nu} \).

References

[1] C. Doran and A.N. Lasenby. Geometric algebra for physicists. Cambridge University Press New York, Cambridge, UK, 1st edition, 2003.

[2] Peeter Joot. Mathematica modules for Geometric Algebra’s GA(2,0), GA(3,0), and GA(1,3), 2017. URL https://github.com/peeterjoot/gapauli. [Online; accessed 24-Oct-2020].

Partisan political spam from the CEO of an expense reporting company

October 22, 2020 Incoherent ramblings No comments , ,

Check out the following unsolicited email that I received at work from the CEO of the expense reporting software that is used by our company:

I know you don’t want to hear this from me. And I guarantee I don’t want to say it. But we are facing an unprecedented attack on the foundations of democracy itself. If you are a US citizen, anything less than a vote for Biden is a vote against democracy.

That’s right, I’m saying a vote for Trump, a vote for a third-party candidate, or simply not voting at all — they’re all the same, and they all mean:

“I care more about my favorite issue than democracy. I believe Trump winning is more important than democracy. I am comfortable standing aside and allowing democracy to be methodically dismantled, in plain sight.”

If the polls are accurate, there’s a roughly 50% chance that you agree Trump needs to go. You know what to do: show up on November 3rd and vote for Biden. Or even better, don’t wait until then: vote today. Go to Vote.org if you need help figuring out how.

The rest of this email is intended to address the concerns of those who disagree, and I’ll try to take the most likely questions in turn:

Q: Why do you care so much about democracy?

Democracy is core to our business success, in a variety of ways. Internally, we are a famously “flat” organization — nobody reports to anyone else, and advancement is the result of meeting well defined criteria as judged by the vote of those who have already advanced. How we compensate each other is left up to a team vote as well. Even our external business model depends on individual employees “electing” to adopt XXXXXXX as individuals, and then “campaigning” internally to get it adopted companywide. At every layer, democracy is our core competitive advantage — both as a company, and as a nation. But that advantage is only as strong as the clarity of our rules and the fairness of their application. Any attempt to disrupt the rules or apply them unfairly is a direct threat to the strength of our company, and the strength of our nation.

Q: What gives you the right to tell me what to do?

The first amendment. To be clear, you don’t need to listen. But the first amendment exists to encourage people like you and me to find some way to talk about the issues that matter, set aside our differences, and find a common ground on which to collectively govern 331 million citizens. Yes democratic self-rule can be inconvenient. But a burden of democracy is that this is literally our job, so I’m asking all of us to take it seriously.

Q: But you’re a company, shouldn’t you remain neutral?

XXXXXXX depends on a functioning society and economy; not many expense reports get filed during a civil war. As CEO of this business, it’s my job to plot a course through any storm — and all evidence suggests that another 4 (or as Trump has hinted — 8, or more?) years of Trump leadership will damage our democracy to such an extent, I’m obligated on behalf of shareholders to take any action I can to avoid it. I am confident our democracy (and XXXXXXX) can survive a Biden presidency. I can’t say the same about Trump. It’s truly as simple as that.

Q: Don’t you think you’re… exaggerating a bit?

I truly wish I was. I wouldn’t be sending this email if this election were just about “normal issues” — taxes, legislative priorities, healthcare, etc. But it isn’t. This election is a referendum on what limits, if any, we place on our elected leaders to govern us in a fair and representative way. This election will decide if widespread voter suppression is an acceptable governing tactic.

Q: Doesn’t everyone suppress votes?

Not like Trump. This is the most heavily litigated election in history, with over 300 lawsuits rushing through the courts before election day. And in every case, Biden is pushing to enable voters while Trump is pushing to suppress them. The trend couldn’t be more clear: Biden wants democracy, Trump does not. A vote for Trump is to endorse voter suppression, it really is very basic. This isn’t about party politics: if Biden were advocating for half of the voter suppression that Trump is actively doing, then I’d be fighting against Biden, too. This is bigger than politics as usual: this is about the very foundation of our nation.

Q: Isn’t Trump just trying to prevent voter fraud?

Voter fraud is virtually nonexistent, as overwhelmingly shown by data showcased by the White House itself. That data comes from the Heritage Foundation, a conservative think tank counting every single known case of voter fraud since 1948, which adds up to only 1,290 distinct votes over 78 years. In 2016 alone there were 138 million votes. There is just no credible argument that voter fraud is significant, even based on Trump’s own data.

Q: Isn’t Biden just using more widespread voting to get elected?

Absolutely. This is the heart of the issue. Biden believes that enabling more people to vote will help him win. Biden wins by promoting democracy; Trump wins by suppressing it. A vote for Biden is a vote for democracy.

Q: So what if Trump gets elected by voter suppression, all’s fair right?

Well that’s what we’re going to decide, on November 3rd. Do you want your elected official to win based on the merits of their ideas? Or based on the ruthlessness of their voter suppression? And if you’re ok with “just a little suppression” — where do you draw the line?

Q: Why send me this when the polls say Biden is going to win?

The polls said Trump was going to lose last time, and he didn’t. But even if the polls can be trusted, that might still not be enough. Trump has stated repeatedly he will only honor an election that he personally feels is fair. So much depending on his personal judgement is worrying, because he has rejected the overwhelming expert consensus that voter fraud has been negligible historically, and has also said he believes it would be impossible to lose a fair election. Accordingly, the only way to ensure a peaceful transition of power is to ensure this election is an overwhelming, undeniable landslide in favor of Biden. Any excuse to question the election is an opportunity for Trump to refuse to leave the White House, plunging this country into a Constitutional crisis bordering on civil war. No matter how slight that risk might be, the consequences of it happening would be so catastrophic to society and the economy, we need to do all we can to prevent it.

So one final plea. As a fellow citizen, I fully support and respect your Constitutional right to disagree — and as an avid supporter of democracy, I value that disagreement. Constructive, well-informed debate (hopefully using the most accurate, least biased news source available) is what makes this nation so exceptional.

But the Constitution is only as strong as the respect we give it. I’m asking you to cherish it close to your heart, and demand that those you elect do the same.

-XXXXX
Founder and CEO of XXXXXXX

PS: Agree or disagree? Reply to this email to share your thoughts with Concierge, or hit me up on Twitter @XXXXXXX to discuss!

PPS: Want to do even more? Support the National Popular Vote to make every vote count equally toward the presidential election, even if you aren’t in one of the 12 states deciding this election.

PPPS: Are you annoyed that you received this as a non-US citizen? If you’re lucky enough to live in a democracy, then I’d encourage you to protect it and be willing to do uncomfortable things — like emailing millions of customers — to defend it.

I found this severely annoying, and fired off the following quick reply:

Shame on you for spamming corporate customers of your company with a politically partisan opinion piece!  I’m just a worker bee in this company, but if I was a purchasing authority, I’d be severely unimpressed.
I’m not a US citizen, but still find this incredibly offensive, not because I agree or disagree, but because of the shear unprofessionalism of your action.  This has no place being pushed out to random people in their workplaces.
Do you really think you will do any good pushing your unsolicited opinion on people when you have no idea what their beliefs are, or the reasons for their decisions, should they be opting to not vote your choice?  I’d expect that what you are doing will just increase polarization, and not have the objective that you are hoping for.  I’d be amused if the actual result of your unsolicited email is to push Trump supporters that were on their butts out of their chairs to the voting booths because they felt that they had to protect their clown from pushy democrats that are sending out panic laden emails like this.
As it happens, I consider both the lead clowns of the US blue and red parties both horrible options.  You aren’t doing your “save democracy” argument much good when you are pushing either option.  If anything, this just serves to illustrate how much of a fraud democracy is.  Perhaps the democratic party should stop repeatedly sabotaging their candidates that have actual popular support?
Are you a US citizen?  It is too bad that Monty Brewster is not running:  “Don’t vote for any of us. We’re assholes! We’ll only make things worse. That’s a promise!”

Lockdowns are starving kids to death

October 20, 2020 Incoherent ramblings No comments , , , , ,

It’s been clear since our petty dictators started imposing COVID lockdowns that these are actions that disproportionately target the poor. I’d been thinking of that in terms of people in the city, waiters, cooks, theater and gym staff, …, who have lost their jobs, will lose their homes, and will rack up debt.  However, this is much more than a first world problem.  There is real cost to blind fear.

Initially we saw many virtue signalling rich celebrities blindly parrot “stay at home” while their personal shoppers and cooks procured their needs.  Later the peons got into the act and made themselves feel good by spouting meaningless catch phrases like  “flatten the curve”, “exponential growth”, “stay safe”, “stay apart”, and “follow the science” (the irony of this last one is amazing!).  Somehow, this was all exploited by media and power hungry politicians to mobilize enough fear that people clamored to have their freedoms taken away, creating illusions of safety.  I  don’t really understand how the COVID fear porn has reached these comprehension defying levels.  The media and politicians who have been pumping the mindless fear really need to step back and take ownership for the chaos, death and misery that will result from their actions.

For months, there have been WHO projections of millions who will die of starvation in developing countries as side effects of lockdown policies.  I had naively envisioned that this would be economic fallout, believing that developing countries would not be foolhardy enough to attempt to replicate the rich country lockdown strategies.  As it turns out, stupidity is more contagious than I imagined it would be, and there are poor countries that have imposed lockdowns on their people, despite the fact that their people have much bigger dangers to battle in their day to day lives.

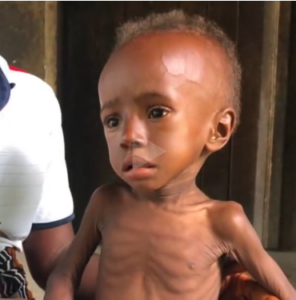
For a taste of this chaos, check out this Tom Woods episode with Gret Glyer, the founder of DonorSee.  The episode talks about lockdowns in Africa that are killing more kids than COVID, and lockdowns in Sierra-Leone that are so severe that kids are not being allowed to get food available across the street.  Crossing the street was prohibited since it would have required them to cross an imaginary line drawn by an idiot bureaucrat. Seeing the images of the skeletal Sierra-Leone kids is heartbreaking.  Gret predicts that despite continual decreases in child mortality over the last 30 years, there will be a massive spike in excess child mortality in 2020. This spike isn’t going to be due to COVID, but because of fear based political responses that are starving kids to death!

Future generations will look back at the pathetic people of 2020, and shake their heads at how uninformed fear and group-think lead to so much death worldwide.  The death that are being focused on are the deaths of those over 80 years old, labelled “covid deaths”.  These are people that generally have multiple pre-existing conditions that were the root cause of the death, with coronaviruses possibly pushing them over the top (and getting the blame.)  Some of those deaths may have been accelerated by COVID, but were likely not preventable.  What could be prevented are all the surplus deaths due to the evil lockdown policies themselves (these deaths in developing countries, deaths by suicide and drug and alcohol abuse in response to financial ruin and demoralization, …).  Children, statistically speaking, are not dying of COVID, but they are being killed by the lockdowns.

It is, incidentally, confusing and heart breaking to be glad that my mother and my mother in law passed away in 2019, and did not live long enough to die this year.  In order to “save grandma” we are consigning family members that are at the end of their lives to die in misery isolated from their families.

[/rant]

Glamping CanyonLands is open for business!

October 15, 2020 Incoherent ramblings No comments

 

My brother and his wife are awesome and fearless. Despite the all the uncertainty and chaos in this climate of dictatorial lockdowns, restrictions and pervasive fear-porn, they have opted to start their own glamping (glamous camping) business, Glamping CanyonLands. They’ve bought a bare bones desert property in Utah that literally had nothing.  They’ve now transformed this nothing into a facility with a washroom and shower (and everything that was required to do so, like water heaters, pumps, septic, …), built parking, and are currently providing three sets of luxury tent accommodations.

This video highlights some of the surroundings and the facilities.  They’ve only been open for a couple of days, but already have a nice set of reviews.

During the night, the location is perfect for viewing the milky way. During the day, it can be your staging area for awesome desert hiking, sightseeing and photography.

Classical mechanics notes on Amazon in paperback (but don’t buy a copy!)

October 13, 2020 math and physics play No comments ,

I have a fairly monstrous set of classical mechanics notes that I accumulated when I was learning all about the theory of Lagrangians, Hamiltonians, and Noether’s theorem.

I also audited a few of the classes from the 2012 session of PHY354H1S, Advanced Classical Mechanics, taught by Prof. Erich Poppitz, at the University of Toronto, and have some notes and problems from those classes in this set of notes.

These notes are not self contained.  In particular, there is fairly heavy use of geometric algebra in many of the problems, with assumptions that the reader is proficient with that algebra.

These notes (436 pages, 6″x9″) are available in the following formats:

  • for free in PDF format (colour),
  • on Amazon in paperback (black and white),
  • as latex sources.

I’ve pressed the publish button on kindle-direct-publishing so that I could get a paper copy of these notes for myself.  An extremely vicious edit is required.  Until I do that editing (assuming I do), the price is set to the absolute minimum no commission price that Amazon let’s me offer (i.e. printing cost plus profit for Amazon.)  I wouldn’t actually recommend that anybody buy this in it’s current form — download the pdf if you are interested.

I’m actually toying with the idea of rewriting these notes from scratch, creating an “Advanced Classical Mechanics, with Geometric Algebra” book out of some of the ideas.  I could flush out many of the details that I explored originally, but add some actual structure and coherence to this mess of write-once-read-none junk.  Tying things to a geometric algebra theme would be the value add proposition that could distinguish things from all the other classical mechanics books in the universe.

That said, this idea would be a very tough book project (for me), as I’d have to understand all the material enough to present it in a coherent fashion.  I’d want to include and explore both Euclidean and relativistic Lagrangians, which would make the material tougher, but comprehensive.  I don’t like the idea of assuming the reader is familiar with special relativity, but the thought of me having to include a self contained introduction to that topic that isn’t complete garbage is pretty intimidating.  Especially if you consider that I’d also want to introduce STA, and help the reader understand the connections between all that material.  There’s a lot of ideas that would all have to come together!

Replacing some wall sconces. Electrical surprise!

October 3, 2020 Uncategorized No comments , , ,

We had some wall sconces in the second floor hallway.  One of them sputtered and we didn’t trust it.  Sofia found some nice replacements a few weeks ago, and today was installation day.

I was rather surprised when I took off the old light and found a wiring hairball.  Here’s a picture after taking off (all but one of) the merretts:

I’d never seen anything like this, not even at my last house, where the previous owner (Mr. C) never found a ground wire that he didn’t like hanging loose.  You can’t really see into the back of the box in that picture, but all the wires are loose (no wiring clips securing the wires to the back of the box). none of the sheathing has been removed, and all the connections were jammed into a single tight cubic inch in an impossibly tangled mess.  The grounds were all tied, but Mr C would have been proud, as none of them were connected to the ground screws at the back of the box.  You can see things a bit better after a bit of unraveling:

Of these wires, I hadn’t yet identified which was switch, which went to the second sconce, and which was the supply.  I’m not sure about other locales, but the Ontario electrical handbook specifies that white is hot at the switch, so looking at this, I think the guess should be that the switch wire is the top left (i.e. when the switch is on, we have supply through the white, to and through the switch, and back through the black where it will power the load.)  That didn’t make sense since the switch is on the right down about a foot.  The only logical wire for the switch would be that bottom one.  I decoupled everything so that I could test the lines (carefully) with the power back on, warning everybody in the house to keep clear:

My tester showed that the top left was the supply, leaving the top right and the left as candidates for the switch and the other sconce.  A couple more trips to the breaker box, and some temporary connections verified what was what, and I was ready to start reconnecting things.  First step was stripping the sheathing off the wires.   I couldn’t use a standard stripping tool, since everything was already in the box, but had to carefully do that with a knife:

I’d never seen anybody not take the sheathing off, which was the major source of the hairball wiring.  This wire was either 12 gauge or just really old, but it was very stiff and hard to handle.  With all the sheathing still on, whoever wired this up originally must have had a hell of a job.  I got the switch’s white connected up to the supply black, and put in some clamps at the back of the box and secured the grounds all physically to the box.

I left one ground long to potentially connect to the new light, but it turned out that the ground wire on the new light was super long, so I ended up trimming that one back and direct connecting it to the back off the box with all the rest, instead of using a merrett for the ground.

Special bonus.

It seemed prudent to open up the switch too, and found that the ghost of Mr C was haunting that too.  Check out the nice floating ground lurking in the switch:

This single pole switch doesn’t have a ground screw, but it just seems really sloppy not to connect that ground to the back of the box.  This wire was also not clamped, so I did that too, and put in a brand new switch while I was at it.

 

EDIT: Before:

After:

My Kiva loan stats and rationale.

October 2, 2020 Incoherent ramblings No comments , ,

For most of the time that I was at IBM (before leaving to LzLabs), I was enrolled in the Employee Charitable Fund (ECF) program.  The ECF was a really easy way to do charitable donations, as the donations were small biweekly payroll deductions.  As all the charitable options were official Canadian charities, I also got that tiny little tax deduction kickback as well.

Despite those benefits, I never really liked the ECF charity options, as it felt like my money was just going into a black hole.  I heard about Kiva on the “How things work” podcast, and decided to bail from the ECF for a while and make some Kiva loans instead.  Kiva is a microloan service, where you can loan selected individuals money in $25 increments.  You get to pick who you want to loan to.  As you get paid back, you can funnel those funds back into new loans.

Switching my funds to Kiva loans isn’t a charitable donation in the traditional sense.  In particular, it doesn’t count as an offical Canadian charitable, so I don’t get any tax kickbacks.  Those are usually just pennies anyways, so that’s not a big loss.  If you are in the US you can get a tax kickback for donations to Kiva itself, but not for your loans.  However, I treat my Kiva account like it’s a one way donation, funneling money in, and recycling all of it into new loans when I get payments.

In a rather timely fashion, as it’s was my end of month “Kiva donation time”, I got a notification of leanpub royalties today:


Leanpub is a pay what you want e-book publishing service that provides the purchasers with automatic updates, and purchaser only forums for Q&A.  I didn’t really expect anybody would buy my stuff on leanpub, since I also make pdfs of all those books available for free.  However, I don’t feel guilty about that for a couple reasons.  One is that the purchaser has freedom to pick their price, and most seem to go over minimum.  The other reason is that I have been funneling my leanpub royalties when I get them into my Kiva account.  Usually, y leanpub sales, as they are batched and sporadic, don’t cover my regular Kiva contributions, but this month, they did.

Having been making kiva loans and contributions for so many years now, I’ve got a pretty decent distribution of countries covered:

I regularly reset my ‘Saved Search’ to remove the most frequently leant to countries, and it looks like it’s time to do that again.

I’m pretty selective about the categories that I select my microloans, and that bias is obvious looking at the distribution of the loan categories I’ve selected:

I particularly like the construction loan category, since I can pick somebody looking for tools to improve their business.  I like the self sustainability of that.

This strategy of small regular loans that feed back on themselves really accumulates nicely.  I’ve been making only small monthly contributions, yet that has added up to $6K of total loans over the years, and I’ve now got $1500 of loans in the pipe.  I’ve lost only about $100, which compared to the management fees of a typical charity, is actually pretty extraordinary.  I’ve also lost a small amounts to donations to Kiva itself.  They are asking for lots per loan these days, and I cheap out those contributions, but that has probably still added up.

%d bloggers like this: