[Click here for a PDF version of this post]
On discord, on the bivector server, ‘stationaryactionprinciple’ asked a question that I really liked.
It’s a question that nagged me before too, but I hadn’t taken the time to puzzle through it properly.
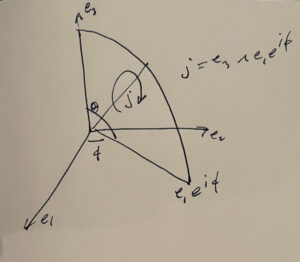
The main character in this question is the spherical polar form of a radial vector, which has the form
\begin{equation}\label{eqn:dexpquestion:20}
\begin{aligned}
i &= \Be_{12} \\
j &= \Be_{31} e^{i\phi} \\
\Bx(r,\theta,\phi) &= r \Be_3 e^{j \theta},
\end{aligned}
\end{equation}
as illustrated in Fig. 1
Notice that all the \( \phi \) dependence comes from the bivector \( j = j(\phi) \), which makes life a bit tricky. We can take \( r, \theta \) or \( \phi \) partials of \( \Bx \), but need to be particularly careful how we do this for the \( \phi \) partials of the exponential factor.
One correct way to compute such a partial is to first expand the exponential in its trig constituents, as
\begin{equation}\label{eqn:dexpquestion:120}
e^{j \theta} = \cos\theta + j \sin\theta,
\end{equation}
and then take the derivative with respect to \(\phi\). If we do so, we get
\begin{equation}\label{eqn:dexpquestion:140}
\PD{\phi}{} e^{j\theta} = \PD{\phi}{j} \sin\theta.
\end{equation}
On the other hand, should we just directly take derivatives of the exponential, one might think that the result is
\begin{equation}\label{eqn:dexpquestion:160}
\PD{\phi}{} e^{j\theta} = \PD{\phi}{(j\theta)} e^{j\theta} = \theta \PD{\phi}{j} e^{j\theta}.
\end{equation}
but this is not correct, for a subtle reason. To understand why, we can step back to the power series representation of the exponential, and compute
\begin{equation}\label{eqn:dexpquestion:60}
\begin{aligned}
\PD{\phi}{e^{j\theta}}
&= \sum_{k = 0}^\infty \PD{\phi}{} \frac{ (j \theta)^k }{k!} \\
&= \sum_{k = 1}^\infty \PD{\phi}{j^k} \frac{ \theta^k }{k!}.
\end{aligned}
\end{equation}
If you treat \( j \) as a complex number, this then reduces to
\begin{equation}\label{eqn:dexpquestion:80}
\begin{aligned}
\PD{\phi}{e^{j\theta}}
&= \sum_{k = 1}^\infty k \PD{\phi}{j} j^{k-1} \frac{ \theta^k }{k!} \\
&=
\theta \PD{\phi}{j} \sum_{k = 1}^\infty \frac{ (j\theta)^{k-1} }{(k-1)!} \\
&=
\theta \PD{\phi}{j} e^{j\theta}.
\end{aligned}
\end{equation}
But, as we have said, this is wrong. The reason that this is wrong is because \( \PDi{\phi}{j} \) does not commute with \( j \), so
\begin{equation}\label{eqn:dexpquestion:100}
\PD{\phi}{j^k} = \PD{\phi}{j} j^{k-1} + j \PD{\phi}{j} j^{k-2} + \cdots,
\end{equation}
not \( k (\PDi{\phi}{j}) j^{k-1} \).
This non-commutativity, sneakily hiding in the power series for the exponential, messes us up. If we are careful, though, we should still be able to compute the correct result using the power series representation of the exponential. To do so, we need to understand the commutation relations for \( j \) and \( j’ \). Writing \( j’ = \PDi{\phi}{j} \), those two bivectors are
\begin{equation}\label{eqn:dexpquestion:180}
\begin{aligned}
j &= \Be_{31} e^{i\phi} \\
j’ &= \Be_{32} e^{i\phi},
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:dexpquestion:200}
\begin{aligned}
j j’
&= \Be_{31} e^{i\phi} \Be_{32} e^{i\phi} \\
&= \Be_{3132} e^{-i\phi} e^{i\phi} \\
&= -\Be_{12},
\end{aligned}
\end{equation}
and
\begin{equation}\label{eqn:dexpquestion:220}
\begin{aligned}
j’ j
&= \Be_{32} e^{i\phi} \Be_{31} e^{i\phi} \\
&= \Be_{3231} e^{-i\phi} e^{i\phi} \\
&= \Be_{12}.
\end{aligned}
\end{equation}
We find that \( j \) and \( j’ \), in this case, anticommute
\begin{equation}\label{eqn:dexpquestion:240}
j j’ = -j’ j.
\end{equation}
We can now compute
\begin{equation}\label{eqn:dexpquestion:260}
\begin{aligned}
\PD{\phi}{j^k}
&= j’ j^{k-1} + j j’ j^{k-2} + j^2 j’ j^{k-3} \cdots \\
&= j’ j^{k-1} – j’ j^{k-1} + (-1)^2 j’ j^{k-1} \cdots
\end{aligned}
\end{equation}
This is zero for any even \( k \) and \( j’ j^{k-1} \) for odd \( k \).
Plugging this back into our Taylor series for the derivative (before we messed it up), we find
\begin{equation}\label{eqn:dexpquestion:280}
\begin{aligned}
\PD{\phi}{e^{j\theta}}
&= \sum_{k = 1, k \in \mathrm{odd}}^\infty j’ j^{k-1} \frac{ \theta^k }{k!} \\
&= j’ \inv{j}
\sum_{k = 1,\, k \in \mathrm{odd}}^\infty \frac{ (j\theta)^k }{k!} \\
&= j’ \inv{j} \sinh( j \theta ) \\
&= j’ \inv{j} j \sin( \theta ) \\
&= j’ \sin( \theta ).
\end{aligned}
\end{equation}
This is exactly the result that we had when we expanded \( e^{j\theta} \) in it’s cis form, and then took derivatives, so we have now reconciled the two different approaches.
Observe that, as a side effect of this exploration, we know also know how to compute the derivative of \( e^{j\theta} \) for the special case where \( j j’ = -j’ j \), which will be the case for any \( j \) where \( j^2 = \mathrm{constant} \).