power series

Derivatives of spherical polar vector representation.

December 6, 2023 math and physics play , , , , ,

[Click here for a PDF version of this post]

On discord, on the bivector server, ‘stationaryactionprinciple’ asked a question that I really liked.
It’s a question that nagged me before too, but I hadn’t taken the time to puzzle through it properly.

The main character in this question is the spherical polar form of a radial vector, which has the form
\begin{equation}\label{eqn:dexpquestion:20}
\begin{aligned}
i &= \Be_{12} \\
j &= \Be_{31} e^{i\phi} \\
\Bx(r,\theta,\phi) &= r \Be_3 e^{j \theta},
\end{aligned}
\end{equation}
as illustrated in Fig. 1

Fig. 1. Spherical polar conventions.

Notice that all the \( \phi \) dependence comes from the bivector \( j = j(\phi) \), which makes life a bit tricky. We can take \( r, \theta \) or \( \phi \) partials of \( \Bx \), but need to be particularly careful how we do this for the \( \phi \) partials of the exponential factor.

One correct way to compute such a partial is to first expand the exponential in its trig constituents, as
\begin{equation}\label{eqn:dexpquestion:120}
e^{j \theta} = \cos\theta + j \sin\theta,
\end{equation}
and then take the derivative with respect to \(\phi\). If we do so, we get
\begin{equation}\label{eqn:dexpquestion:140}
\PD{\phi}{} e^{j\theta} = \PD{\phi}{j} \sin\theta.
\end{equation}
On the other hand, should we just directly take derivatives of the exponential, one might think that the result is
\begin{equation}\label{eqn:dexpquestion:160}
\PD{\phi}{} e^{j\theta} = \PD{\phi}{(j\theta)} e^{j\theta} = \theta \PD{\phi}{j} e^{j\theta}.
\end{equation}
but this is not correct, for a subtle reason. To understand why, we can step back to the power series representation of the exponential, and compute
\begin{equation}\label{eqn:dexpquestion:60}
\begin{aligned}
\PD{\phi}{e^{j\theta}}
&= \sum_{k = 0}^\infty \PD{\phi}{} \frac{ (j \theta)^k }{k!} \\
&= \sum_{k = 1}^\infty \PD{\phi}{j^k} \frac{ \theta^k }{k!}.
\end{aligned}
\end{equation}
If you treat \( j \) as a complex number, this then reduces to
\begin{equation}\label{eqn:dexpquestion:80}
\begin{aligned}
\PD{\phi}{e^{j\theta}}
&= \sum_{k = 1}^\infty k \PD{\phi}{j} j^{k-1} \frac{ \theta^k }{k!} \\
&=
\theta \PD{\phi}{j} \sum_{k = 1}^\infty \frac{ (j\theta)^{k-1} }{(k-1)!} \\
&=
\theta \PD{\phi}{j} e^{j\theta}.
\end{aligned}
\end{equation}
But, as we have said, this is wrong. The reason that this is wrong is because \( \PDi{\phi}{j} \) does not commute with \( j \), so
\begin{equation}\label{eqn:dexpquestion:100}
\PD{\phi}{j^k} = \PD{\phi}{j} j^{k-1} + j \PD{\phi}{j} j^{k-2} + \cdots,
\end{equation}
not \( k (\PDi{\phi}{j}) j^{k-1} \).

This non-commutativity, sneakily hiding in the power series for the exponential, messes us up. If we are careful, though, we should still be able to compute the correct result using the power series representation of the exponential. To do so, we need to understand the commutation relations for \( j \) and \( j’ \). Writing \( j’ = \PDi{\phi}{j} \), those two bivectors are
\begin{equation}\label{eqn:dexpquestion:180}
\begin{aligned}
j &= \Be_{31} e^{i\phi} \\
j’ &= \Be_{32} e^{i\phi},
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:dexpquestion:200}
\begin{aligned}
j j’
&= \Be_{31} e^{i\phi} \Be_{32} e^{i\phi} \\
&= \Be_{3132} e^{-i\phi} e^{i\phi} \\
&= -\Be_{12},
\end{aligned}
\end{equation}
and
\begin{equation}\label{eqn:dexpquestion:220}
\begin{aligned}
j’ j
&= \Be_{32} e^{i\phi} \Be_{31} e^{i\phi} \\
&= \Be_{3231} e^{-i\phi} e^{i\phi} \\
&= \Be_{12}.
\end{aligned}
\end{equation}
We find that \( j \) and \( j’ \), in this case, anticommute
\begin{equation}\label{eqn:dexpquestion:240}
j j’ = -j’ j.
\end{equation}
We can now compute
\begin{equation}\label{eqn:dexpquestion:260}
\begin{aligned}
\PD{\phi}{j^k}
&= j’ j^{k-1} + j j’ j^{k-2} + j^2 j’ j^{k-3} \cdots \\
&= j’ j^{k-1} – j’ j^{k-1} + (-1)^2 j’ j^{k-1} \cdots
\end{aligned}
\end{equation}
This is zero for any even \( k \) and \( j’ j^{k-1} \) for odd \( k \).

Plugging this back into our Taylor series for the derivative (before we messed it up), we find
\begin{equation}\label{eqn:dexpquestion:280}
\begin{aligned}
\PD{\phi}{e^{j\theta}}
&= \sum_{k = 1, k \in \mathrm{odd}}^\infty j’ j^{k-1} \frac{ \theta^k }{k!} \\
&= j’ \inv{j}
\sum_{k = 1,\, k \in \mathrm{odd}}^\infty \frac{ (j\theta)^k }{k!} \\
&= j’ \inv{j} \sinh( j \theta ) \\
&= j’ \inv{j} j \sin( \theta ) \\
&= j’ \sin( \theta ).
\end{aligned}
\end{equation}
This is exactly the result that we had when we expanded \( e^{j\theta} \) in it’s cis form, and then took derivatives, so we have now reconciled the two different approaches.

Observe that, as a side effect of this exploration, we know also know how to compute the derivative of \( e^{j\theta} \) for the special case where \( j j’ = -j’ j \), which will be the case for any \( j \) where \( j^2 = \mathrm{constant} \).

PHY1520H Graduate Quantum Mechanics. Lecture 20: Perturbation theory. Taught by Prof. Arun Paramekanti

December 3, 2015 phy1520 , , , , , , , , , ,

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

These are notes for the UofT course PHY1520, Graduate Quantum Mechanics, taught by Prof. Paramekanti, covering [1] ch. 5 content.

Perturbation theory

Given a \( 2 \times 2 \) Hamiltonian \( H = H_0 + V \), where

\begin{equation}\label{eqn:qmLecture20:20}
H =
\begin{bmatrix}
a & c \\
c^\conj & b
\end{bmatrix}
\end{equation}

which has eigenvalues

\begin{equation}\label{eqn:qmLecture20:40}
\lambda_\pm = \frac{a + b}{2} \pm \sqrt{ \lr{ \frac{a – b}{2}}^2 + \Abs{c}^2 }.
\end{equation}

If \( c = 0 \),

\begin{equation}\label{eqn:qmLecture20:60}
H_0 =
\begin{bmatrix}
a & 0 \\
0 & b
\end{bmatrix},
\end{equation}

so

\begin{equation}\label{eqn:qmLecture20:80}
V =
\begin{bmatrix}
0 & c \\
c^\conj & 0
\end{bmatrix}.
\end{equation}

Suppose that \( \Abs{c} \ll \Abs{a – b} \), then

\begin{equation}\label{eqn:qmLecture20:100}
\lambda_\pm \approx \frac{a + b}{2} \pm \Abs{ \frac{a – b}{2} } \lr{ 1 + 2 \frac{\Abs{c}^2}{\Abs{a – b}^2} }.
\end{equation}

If \( a > b \), then

\begin{equation}\label{eqn:qmLecture20:120}
\lambda_\pm \approx \frac{a + b}{2} \pm \frac{a – b}{2} \lr{ 1 + 2 \frac{\Abs{c}^2}{\lr{a – b}^2} }.
\end{equation}

\begin{equation}\label{eqn:qmLecture20:140}
\begin{aligned}
\lambda_{+}
&= \frac{a + b}{2} + \frac{a – b}{2} \lr{ 1 + 2 \frac{\Abs{c}^2}{\lr{a – b}^2} } \\
&= a + \lr{a – b} \frac{\Abs{c}^2}{\lr{a – b}^2} \\
&= a + \frac{\Abs{c}^2}{a – b},
\end{aligned}
\end{equation}

and
\begin{equation}\label{eqn:qmLecture20:680}
\begin{aligned}
\lambda_{-}
&= \frac{a + b}{2} – \frac{a – b}{2} \lr{ 1 + 2 \frac{\Abs{c}^2}{\lr{a – b}^2} } \\
&=
b + \lr{a – b} \frac{\Abs{c}^2}{\lr{a – b}^2} \\
&= b + \frac{\Abs{c}^2}{a – b}.
\end{aligned}
\end{equation}

This adiabatic evolution displays a “level repulsion”, quadradic in \( \Abs{c} \) as sketched in fig. 1, and is described as a non-degenerate perbutation.

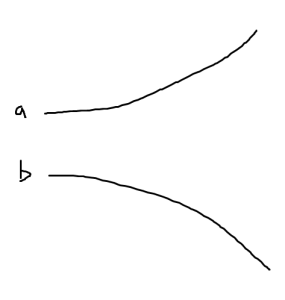
fig. 1. Adiabatic (non-degenerate) perturbation

fig. 1. Adiabatic (non-degenerate) perturbation

If \( \Abs{c} \gg \Abs{a -b} \), then

\begin{equation}\label{eqn:qmLecture20:160}
\begin{aligned}
\lambda_\pm
&= \frac{a + b}{2} \pm \Abs{c} \sqrt{ 1 + \inv{\Abs{c}^2} \lr{ \frac{a – b}{2}}^2 } \\
&\approx \frac{a + b}{2} \pm \Abs{c} \lr{ 1 + \inv{2 \Abs{c}^2} \lr{ \frac{a – b}{2}}^2 } \\
&= \frac{a + b}{2} \pm \Abs{c} \pm \frac{\lr{a – b}^2}{8 \Abs{c}}.
\end{aligned}
\end{equation}

Here we loose the adiabaticity, and have “level repulsion” that is linear in \( \Abs{c} \), as sketched in fig. 2. We no longer have the sign of \( a – b \) in the expansion. This is described as a degenerate perbutation.

fig. 2. Degenerate perbutation

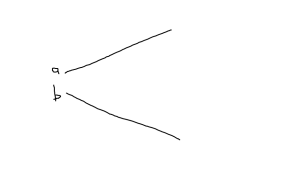
fig. 2. Degenerate perbutation

General non-degenerate perturbation

Given an unperturbed system with solutions of the form

\begin{equation}\label{eqn:qmLecture20:180}
H_0 \ket{n^{(0)}} = E_n^{(0)} \ket{n^{(0)}},
\end{equation}

we want to solve the perturbed Hamiltonian equation

\begin{equation}\label{eqn:qmLecture20:200}
\lr{ H_0 + \lambda V } \ket{ n } = \lr{ E_n^{(0)} + \Delta n } \ket{n}.
\end{equation}

Here \( \Delta n \) is an energy shift as that goes to zero as \( \lambda \rightarrow 0 \). We can write this as

\begin{equation}\label{eqn:qmLecture20:220}
\lr{ E_n^{(0)} – H_0 } \ket{ n } = \lr{ \lambda V – \Delta_n } \ket{n}.
\end{equation}

We are hoping to iterate with application of the inverse to an initial estimate of \( \ket{n} \)

\begin{equation}\label{eqn:qmLecture20:240}
\ket{n} = \lr{ E_n^{(0)} – H_0 }^{-1} \lr{ \lambda V – \Delta_n } \ket{n}.
\end{equation}

This gets us into trouble if \( \lambda \rightarrow 0 \), which can be fixed by using

\begin{equation}\label{eqn:qmLecture20:260}
\ket{n} = \lr{ E_n^{(0)} – H_0 }^{-1} \lr{ \lambda V – \Delta_n } \ket{n} + \ket{ n^{(0)} },
\end{equation}

which can be seen to be a solution to \ref{eqn:qmLecture20:220}. We want to ask if

\begin{equation}\label{eqn:qmLecture20:280}
\lr{ \lambda V – \Delta_n } \ket{n} ,
\end{equation}

contains a bit of \( \ket{ n^{(0)} } \)? To determine this act with \( \bra{n^{(0)}} \) on the left

\begin{equation}\label{eqn:qmLecture20:300}
\begin{aligned}
\bra{ n^{(0)} } \lr{ \lambda V – \Delta_n } \ket{n}
&=
\bra{ n^{(0)} } \lr{ E_n^{(0)} – H_0 } \ket{n} \\
&=
\lr{ E_n^{(0)} – E_n^{(0)} } \braket{n^{(0)}}{n} \\
&=
0.
\end{aligned}
\end{equation}

This shows that \( \ket{n} \) is entirely orthogonal to \( \ket{n^{(0)}} \).

Define a projection operator

\begin{equation}\label{eqn:qmLecture20:320}
P_n = \ket{n^{(0)}}\bra{n^{(0)}},
\end{equation}

which has the idempotent property \( P_n^2 = P_n \) that we expect of a projection operator.

Define a rejection operator
\begin{equation}\label{eqn:qmLecture20:340}
\overline{{P}}_n
= 1 –
\ket{n^{(0)}}\bra{n^{(0)}}
= \sum_{m \ne n}
\ket{m^{(0)}}\bra{m^{(0)}}.
\end{equation}

Because \( \ket{n} \) has no component in the direction \( \ket{n^{(0)}} \), the rejection operator can be inserted much like we normally do with the identity operator, yielding

\begin{equation}\label{eqn:qmLecture20:360}
\ket{n}’ = \lr{ E_n^{(0)} – H_0 }^{-1} \overline{{P}}_n \lr{ \lambda V – \Delta_n } \ket{n} + \ket{ n^{(0)} },
\end{equation}

valid for any initial \( \ket{n} \).

Power series perturbation expansion

Instead of iterating, suppose that the unknown state and unknown energy difference operator can be expanded in a \( \lambda \) power series, say

\begin{equation}\label{eqn:qmLecture20:380}
\ket{n}
=
\ket{n_0}
+ \lambda \ket{n_1}
+ \lambda^2 \ket{n_2}
+ \lambda^3 \ket{n_3} + \cdots
\end{equation}

and

\begin{equation}\label{eqn:qmLecture20:400}
\Delta_{n} = \Delta_{n_0}
+ \lambda \Delta_{n_1}
+ \lambda^2 \Delta_{n_2}
+ \lambda^3 \Delta_{n_3} + \cdots
\end{equation}

We usually interpret functions of operators in terms of power series expansions. In the case of \( \lr{ E_n^{(0)} – H_0 }^{-1} \), we have a concrete interpretation when acting on one of the unpertubed eigenstates

\begin{equation}\label{eqn:qmLecture20:420}
\inv{ E_n^{(0)} – H_0 } \ket{m^{(0)}} =
\inv{ E_n^{(0)} – E_m^0 } \ket{m^{(0)}}.
\end{equation}

This gives

\begin{equation}\label{eqn:qmLecture20:440}
\ket{n}
=
\inv{ E_n^{(0)} – H_0 }
\sum_{m \ne n}
\ket{m^{(0)}}\bra{m^{(0)}}
\lr{ \lambda V – \Delta_n } \ket{n} + \ket{ n^{(0)} },
\end{equation}

or

\begin{equation}\label{eqn:qmLecture20:460}
\boxed{
\ket{n}
=
\ket{ n^{(0)} }
+
\sum_{m \ne n}
\frac{\ket{m^{(0)}}\bra{m^{(0)}}}
{
E_n^{(0)} – E_m^{(0)}
}
\lr{ \lambda V – \Delta_n } \ket{n}.
}
\end{equation}

From \ref{eqn:qmLecture20:220}, note that

\begin{equation}\label{eqn:qmLecture20:500}
\Delta_n =
\frac{\bra{n^{(0)}} \lambda V \ket{n}}{\braket{n^0}{n}},
\end{equation}

however, we will normalize by setting \( \braket{n^0}{n} = 1 \), so

\begin{equation}\label{eqn:qmLecture20:521}
\boxed{
\Delta_n =
\bra{n^{(0)}} \lambda V \ket{n}.
}
\end{equation}

to \( O(\lambda^0) \)

If all \( \lambda^n, n > 0 \) are zero, then we have

\label{eqn:qmLecture20:780}
\begin{equation}\label{eqn:qmLecture20:740}
\ket{n_0}
=
\ket{ n^{(0)} }
+
\sum_{m \ne n}
\frac{\ket{m^{(0)}}\bra{m^{(0)}}}
{
E_n^{(0)} – E_m^{(0)}
}
\lr{ – \Delta_{n_0} } \ket{n_0}
\end{equation}
\begin{equation}\label{eqn:qmLecture20:800}
\Delta_{n_0} \braket{n^{(0)}}{n_0} = 0
\end{equation}

so

\begin{equation}\label{eqn:qmLecture20:540}
\begin{aligned}
\ket{n_0} &= \ket{n^{(0)}} \\
\Delta_{n_0} &= 0.
\end{aligned}
\end{equation}

to \( O(\lambda^1) \)

Requiring identity for all \( \lambda^1 \) terms means

\begin{equation}\label{eqn:qmLecture20:760}
\ket{n_1} \lambda
=
\sum_{m \ne n}
\frac{\ket{m^{(0)}}\bra{m^{(0)}}}
{
E_n^{(0)} – E_m^{(0)}
}
\lr{ \lambda V – \Delta_{n_1} \lambda } \ket{n_0},
\end{equation}

so

\begin{equation}\label{eqn:qmLecture20:560}
\ket{n_1}
=
\sum_{m \ne n}
\frac{
\ket{m^{(0)}} \bra{ m^{(0)}}
}
{
E_n^{(0)} – E_m^{(0)}
}
\lr{ V – \Delta_{n_1} } \ket{n_0}.
\end{equation}

With the assumption that \( \ket{n^{(0)}} \) is normalized, and with the shorthand

\begin{equation}\label{eqn:qmLecture20:600}
V_{m n} = \bra{ m^{(0)}} V \ket{n^{(0)}},
\end{equation}

that is

\begin{equation}\label{eqn:qmLecture20:580}
\begin{aligned}
\ket{n_1}
&=
\sum_{m \ne n}
\frac{
\ket{m^{(0)}}
}
{
E_n^{(0)} – E_m^{(0)}
}
V_{m n}
\\
\Delta_{n_1} &= \bra{ n^{(0)} } V \ket{ n^0} = V_{nn}.
\end{aligned}
\end{equation}

to \( O(\lambda^2) \)

The second order perturbation states are found by selecting only the \( \lambda^2 \) contributions to

\begin{equation}\label{eqn:qmLecture20:820}
\lambda^2 \ket{n_2}
=
\sum_{m \ne n}
\frac{\ket{m^{(0)}}\bra{m^{(0)}}}
{
E_n^{(0)} – E_m^{(0)}
}
\lr{ \lambda V – (\lambda \Delta_{n_1} + \lambda^2 \Delta_{n_2}) }
\lr{
\ket{n_0}
+ \lambda \ket{n_1}
}.
\end{equation}

Because \( \ket{n_0} = \ket{n^{(0)}} \), the \( \lambda^2 \Delta_{n_2} \) is killed, leaving

\begin{equation}\label{eqn:qmLecture20:840}
\begin{aligned}
\ket{n_2}
&=
\sum_{m \ne n}
\frac{\ket{m^{(0)}}\bra{m^{(0)}}}
{
E_n^{(0)} – E_m^{(0)}
}
\lr{ V – \Delta_{n_1} }
\ket{n_1} \\
&=
\sum_{m \ne n}
\frac{\ket{m^{(0)}}\bra{m^{(0)}}}
{
E_n^{(0)} – E_m^{(0)}
}
\lr{ V – \Delta_{n_1} }
\sum_{l \ne n}
\frac{
\ket{l^{(0)}}
}
{
E_n^{(0)} – E_l^{(0)}
}
V_{l n},
\end{aligned}
\end{equation}

which can be written as

\begin{equation}\label{eqn:qmLecture20:620}
\ket{n_2}
=
\sum_{l,m \ne n}
\ket{m^{(0)}}
\frac{V_{m l} V_{l n}}
{
\lr{ E_n^{(0)} – E_m^{(0)} }
\lr{ E_n^{(0)} – E_l^{(0)} }
}
–
\sum_{m \ne n}
\ket{m^{(0)}}
\frac{V_{n n} V_{m n}}
{
\lr{ E_n^{(0)} – E_m^{(0)} }^2
}.
\end{equation}

For the second energy perturbation we have

\begin{equation}\label{eqn:qmLecture20:860}
\lambda^2 \Delta_{n_2} =
\bra{n^{(0)}} \lambda V \lr{ \lambda \ket{n_1} },
\end{equation}

or

\begin{equation}\label{eqn:qmLecture20:880}
\begin{aligned}
\Delta_{n_2}
&=
\bra{n^{(0)}} V \ket{n_1} \\
&=
\bra{n^{(0)}} V
\sum_{m \ne n}
\frac{
\ket{m^{(0)}}
}
{
E_n^{(0)} – E_m^{(0)}
}
V_{m n}.
\end{aligned}
\end{equation}

That is

\begin{equation}\label{eqn:qmLecture20:900}
\Delta_{n_2}
=
\sum_{m \ne n} \frac{V_{n m} V_{m n} }{E_n^{(0)} – E_m^{(0)}}.
\end{equation}

to \( O(\lambda^3) \)

Similarily, it can be shown that

\begin{equation}\label{eqn:qmLecture20:640}
\Delta_{n_3} =
\sum_{l, m \ne n} \frac{V_{n m} V_{m l} V_{l n} }{
\lr{ E_n^{(0)} – E_m^{(0)} }
\lr{ E_n^{(0)} – E_l^{(0)} }
}
–
\sum_{ m \ne n} \frac{V_{n m} V_{n n} V_{m n} }{
\lr{ E_n^{(0)} – E_m^{(0)} }^2
}.
\end{equation}

In general, the energy perturbation is given by

\begin{equation}\label{eqn:qmLecture20:660}
\Delta_n^{(l)} = \bra{n^{(0)}} V \ket{n^{(l-1)}}.
\end{equation}

References

[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.