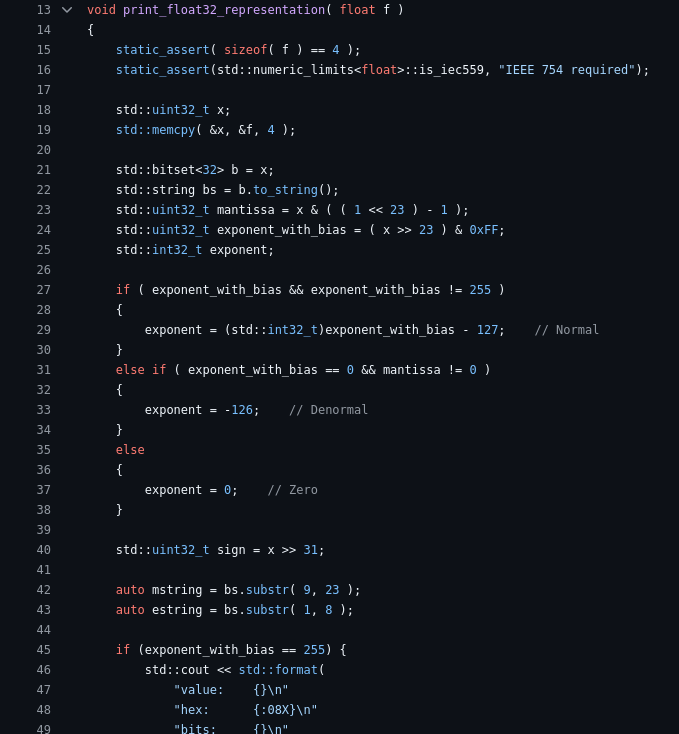
Over the last 8 years, I’ve been intimately involved in building a pair of LLVM based compilers for the COBOL and PL/I languages. However, a lot of my work was on the runtime side of the story. This was non-trivial work, with lots of complex interactions to figure out, but it also meant that I didn’t get to play with the fun (codegen) part of the compiler.
Over the last month or so, I’ve been incrementally building an MLIR based compiler for a toy language. I thought this would be a great way to get my hands dirty, and learn as I went. These were the elements required:
- A lexer/parser grammar for my language, and parse tree walker. I used an altlr4 grammar for this part, emitting C++ parse listener classes.
- An MLIR dialect (tablegen definitions) for the language.
- Parse tree listener callbacks to do the MLIR builder calls.
- Tablegen definitions for the LLVM IR lowering pass.
- Lowering classes for all the required operations.
- A compiler driver to orchestrate all the interconnected pieces, and drive the assembly printer.
As it turns out, MLIR tablegen is pretty finicky when you have no clue what you are doing. Once you get the basic infrastructure in place it makes a lot more sense, and you can look at the generated C++ classes associated with your tablegen, to get a good idea what is happening under the covers.
Here’s a couple examples that illustrate the toy language:
// empty.toy
// This should be allowed by the grammar.
// dcl.toy
DCL x; // the next simplest non-empty program (i.e.: also has a comment)
// foo.toy
DCL x;
x = 3;
// This indenting is to test location generation, and to verify that the resulting columnar position is right.
PRINT x;
// unary.toy
DCL x;
x = 3;
x = +x;
x = -x;
PRINT x;
// test.toy
DCL x;
DCL y;
x = 5 + 3;
y = x * 2;
PRINT x;
There is also a RETURN statement, not in any of those examples explicitly. I added that language element to simplify the LLVM lowering process. Here’s a motivating example:
> ../build/toycalculator empty.toy --location
"builtin.module"() ({
"toy.program"() ({
^bb0:
}) : () -> () loc(#loc1)
}) : () -> () loc(#loc)
#loc = loc(unknown)
#loc1 = loc("empty.toy":2:1)
Notice the wierd looking ‘^bb0:’ in the MLIR dump. This is a representation of an empty basic block, and was a bit of a pain to figure out how to lower properly. What I ended up doing is inserting a RETURN operation into the program if there was no other statements. I wanted to support such a dumb trivial program with no actual statements as a first test for the lowering, and see that things worked end to end before getting some of the trickier lowering working. With a return statement, empty.toy’s MLIR now looks like:
"builtin.module"() ({
"toy.program"() ({
"toy.return"() : () -> () loc(#loc1)
}) : () -> () loc(#loc1)
}) : () -> () loc(#loc)
#loc = loc(unknown)
#loc1 = loc("../samples/empty.toy":2:1)
The idea behind the lowering operations is that each MLIR operation can be matched with a rewriter operation, and the program can be iterated over, gradually replacing all the MLIR operators with LLVM operations.
For example, an element like:
Can be replaced by
Once that replacement is made, we can delete the toy.return element:
// Lower toy.return to nothing (erase).
class ReturnOpLowering : public ConversionPattern
{
public:
ReturnOpLowering( MLIRContext* context )
: ConversionPattern( toy::ReturnOp::getOperationName(), 1, context )
{
}
LogicalResult matchAndRewrite(
Operation* op, ArrayRef operands,
ConversionPatternRewriter& rewriter ) const override
{
LLVM_DEBUG( llvm::dbgs()
<< "Lowering toy.return: " << *op << '\n' );
// ...
rewriter.eraseOp( op );
return success();
}
};
In the sample above the toy.program elememt also needs to be deleted. It gets replaced by a llvm basic block, moving all the MLIR BB elements into it. The last step is the removal of the outer most MLIR module, but there’s an existing Dialect for that. When all is said and done, we are left with the following LLVM IR:
Here’s the MLIR for the foo.toy, which is slightly more interesting
"builtin.module"() ({
"toy.program"() ({
%0 = "memref.alloca"() <{operandSegmentSizes = array}> : () -> memref
"toy.declare"() <{name = "x"}> : () -> ()
%1 = "arith.constant"() <{value = 3 : i64}> : () -> i64
%2 = "toy.unary"(%1) <{op = "+"}> : (i64) -> f64
"memref.store"(%2, %0) : (f64, memref) -> ()
"toy.assign"(%2) <{name = "x"}> : (f64) -> ()
"toy.print"(%0) : (memref) -> ()
"toy.return"() : () -> ()
}) : () -> ()
}) : () -> ()
As we go through the lowering replacements, more an more of the MLIR operators get replaced with LLVM equivalents. Here’s an example part way through:
"llvm.func"() <{CConv = #llvm.cconv, function_type = !llvm.func, linkage = #llvm.linkage, sym_name = "main", visibility_ = 0 : i64}> ({
%0 = "llvm.mlir.constant"() <{value = 1 : i64}> : () -> i64
%1 = "llvm.alloca"(%0) <{alignment = 8 : i64, elem_type = f64}> : (i64) -> !llvm.ptr
%2 = "memref.alloca"() <{operandSegmentSizes = array}> : () -> memref
"toy.declare"() <{name = "x"}> : () -> ()
%3 = "llvm.mlir.constant"() <{value = 3 : i64}> : () -> i64
%4 = "arith.constant"() <{value = 3 : i64}> : () -> i64
%5 = "toy.unary"(%4) <{op = "+"}> : (i64) -> f64
"memref.store"(%5, %2) : (f64, memref) -> ()
"toy.assign"(%5) <{name = "x"}> : (f64) -> ()
"toy.print"(%2) : (memref) -> ()
"toy.return"() : () -> ()
}) : () -> ()
and after a few more:
"llvm.func"() <{CConv = #llvm.cconv, function_type = !llvm.func, linkage = #llvm.linkage, sym_na
me = "main", visibility_ = 0 : i64}> ({
%0 = "llvm.mlir.constant"() <{value = 1 : i64}> : () -> i64
%1 = "llvm.alloca"(%0) <{alignment = 8 : i64, elem_type = f64}> : (i64) -> !llvm.ptr
%2 = "memref.alloca"() <{operandSegmentSizes = array}> : () -> memref
"toy.declare"() <{name = "x"}> : () -> ()
%3 = "llvm.mlir.constant"() <{value = 3 : i64}> : () -> i64
%4 = "arith.constant"() <{value = 3 : i64}> : () -> i64
%5 = "llvm.sitofp"(%3) : (i64) -> f64
%6 = "toy.unary"(%4) <{op = "+"}> : (i64) -> f64
"llvm.store"(%5, %1) <{ordering = 0 : i64}> : (f64, !llvm.ptr) -> ()
"memref.store"(%6, %2) : (f64, memref) -> ()
"toy.assign"(%6) <{name = "x"}> : (f64) -> ()
%7 = "llvm.load"(%1) <{ordering = 0 : i64}> : (!llvm.ptr) -> f64
"llvm.call"(%7) <{CConv = #llvm.cconv, TailCallKind = #llvm.tailcallkind, callee = @__toy_print, fastmathFlags = #llvm.fastmath, op_bundle_sizes = array, operandSegmentSizes = array}> : (f64) -> ()
"toy.print"(%2) : (memref) -> ()
%8 = "llvm.mlir.constant"() <{value = 0 : i32}> : () -> i32
"llvm.return"(%8) : (i32) -> ()
"toy.return"() : () -> ()
}) : () -> ()
Eventually, after various LLVM IR blocks get merged (almost magically by one of the passes), we end up with:
declare void @__toy_print(double)
define i32 @main() {
%1 = alloca double, i64 1, align 8
store double 3.000000e+00, ptr %1, align 8
%2 = load double, ptr %1, align 8
call void @__toy_print(double %2)
ret i32 0
}
Enabling an assembly printer pass, we get an object file
fedora:/home/pjoot/toycalculator/samples> objdump -dr foo.o foo.o: file format elf64-x86-64 Disassembly of section .text: 0000000000000000
fedora:/home/pjoot/toycalculator/samples> ../build/toycalculator foo.toy Generated object file: foo.o fedora:/home/pjoot/toycalculator/samples> clang -o foo foo.o -L ../build -l toy_runtime -Wl,-rpath,`pwd`/../build fedora:/home/pjoot/toycalculator/samples> ./foo 3.000000
A month of work and 1800 lines of code, and now I can print a single constant number!